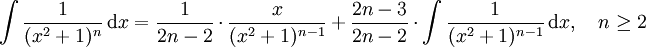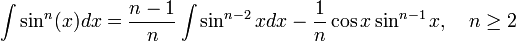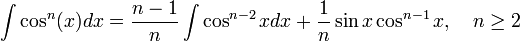- Grundintegrale
-
Diese Tabelle von Ableitungs- und Stammfunktionen (Integraltafel) gibt eine Übersicht über Ableitungsfunktionen und Stammfunktionen, die in der Differential- und Integralrechnung benötigt werden.
Inhaltsverzeichnis
Tabelle einfacher Ableitungs- und Stammfunktionen (Grundintegrale)
Diese Tabelle ist zweispaltig aufgebaut. In der linken Spalte steht die Ableitung der Funktion in der rechten Spalte, umgekehrt ist die Funktion in der rechten Spalte eine Stammfunktion der Funktion in der linken Spalte.
Hinweis: Wenn F(x) eine Stammfunktion von f(x) ist, dann ist auch für jede Konstante C die Funktion F(x) + C eine Stammfunktion von f(x). Zum Beispiel ist auch
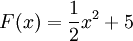 eine Stammfunktion von f(x) = x. Die additive Konstante C wird aus Gründen der Übersichtlichkeit nicht aufgeführt. Weiterhin gilt: Falls F(x) eine Stammfunktion von f(x) ist, so ist aufgrund der Linearität des Integrals
eine Stammfunktion von f(x) = x. Die additive Konstante C wird aus Gründen der Übersichtlichkeit nicht aufgeführt. Weiterhin gilt: Falls F(x) eine Stammfunktion von f(x) ist, so ist aufgrund der Linearität des Integrals 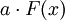 eine Stammfunktion von
eine Stammfunktion von 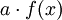 .
.Potenz- und Wurzelfunktionen
Funktion f(x) Stammfunktion F(x) 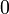
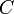
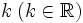
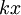
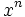
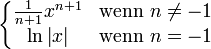
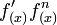
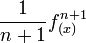
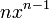
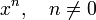
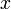
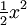
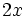
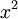
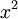
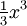
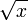
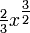
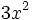
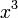
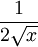
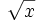
![\frac{1}{n (\sqrt[n]{x})^{n-1}}\;](/pictures/dewiki/98/b4b0ded0de0cf0eac12f067b8ca4b514.png)
![\sqrt[n]{x}\;](/pictures/dewiki/49/1c5be735091462f1ae9783c114756fbe.png)
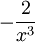
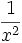
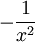
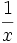
Exponential- und Logarithmusfunktionen
Funktion f(x) Stammfunktion F(x) 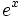
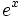
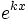
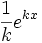
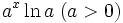
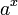
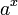
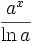
xx(1 + ln(x)) xx (x > 0) 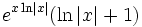
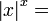
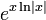
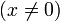
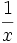
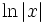
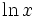
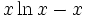
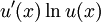
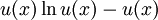
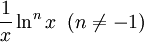
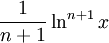
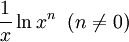
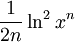
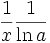
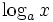
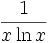
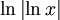 für (x > 0, x ≠ 1)
für (x > 0, x ≠ 1)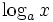
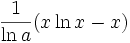
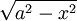
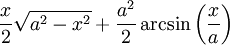
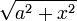
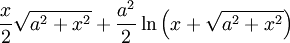
Trigonometrische und Hyperbelfunktionen
Funktion f(x) Stammfunktion F(x) 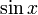
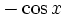
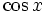
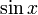
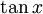
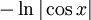
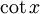
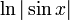
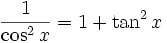
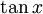
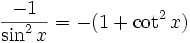
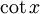
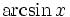
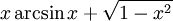
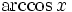
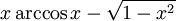
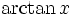
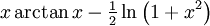
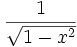
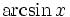
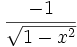
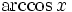
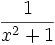
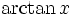
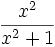
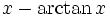
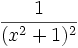
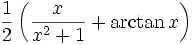
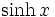
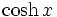
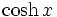
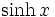
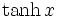
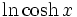
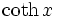
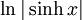
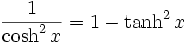
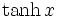
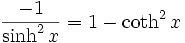
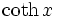
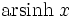
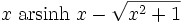
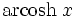
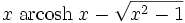
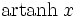
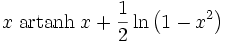
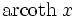
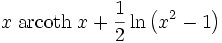
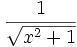
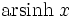
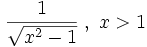
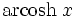
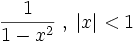
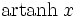
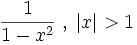
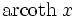
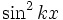
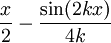
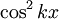
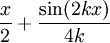
Sonstige
Funktion f(x) Stammfunktion F(x) 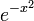
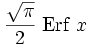
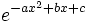
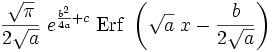
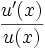
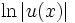
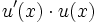
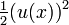
Rekursionsformeln für weitere Stammfunktionen
Weblinks
Wikimedia Foundation.