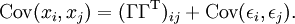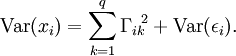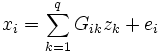Hauptfaktorenanalyse

Die Faktorenanalyse, häufig auch Faktoranalyse, ist ein Verfahren der multivariaten Statistik. Es dient dazu, aus empirischen Beobachtungen verschiedener manifester Variablen (Observablen) auf zugrunde liegende latente Variable („Faktoren“) zu schließen. Sie gehört somit zu den datenreduzierenden (auch dimensionsreduzierenden) inferenz-statistischen Verfahren.

Hintergrund

Geschichte

Die Faktorenanalyse wurde vom Psychologen Charles Spearman für die Auswertung von Intelligenztests entwickelt. 1904 zeigte er, dass Testergebnisse zu einem guten Teil durch ein eindimensionales Persönlichkeitsmerkmal, den general factor (g-Faktor), erklärt werden konnten. Die Verallgemeinerung auf eine Analyse mit mehreren Faktoren wird J. C. Maxwell Garnett zugeschrieben (Steiger 1979); popularisiert wurde sie in den 1940er Jahren von Louis Leon Thurstone.

Maximum-Likelihood-Schätzmethoden wurden in den 1930er und 40er Jahren von Lawley und Victor Barnett vorgeschlagen; ein stabiler Algorithmus wurde in den 1960ern von Karl Gustav Jöreskog entwickelt (Krzanowski, S. 487).

Bis heute wird jedoch trotz schlechter Konvergenzeigenschaften auch eine iterative Variante der Hauptkomponentenanalyse zur Faktorenextraktion eingesetzt. Ungenauigkeiten bis hin zur völligen Gleichsetzung von Faktoren- und Hauptkomponentenanalyse sind weit verbreitet.

Anwendungen

Die Faktorenanalyse ist ein universell einsetzbares Werkzeug, um von den sichtbaren Erscheinungen auf die diesen Erscheinungen zugrunde liegenden unbeobachtbaren Ursachen zu schließen. So sind zum Beispiel Konstrukte wie "Intelligenz" oder "Ehrgeiz" nicht messbar, werden aber als Ursache vieler Verhaltensweisen angesehen.

Gelegentlich wird die Faktorenanalyse auch für naturwissenschaftliche Probleme eingesetzt. Es gibt Beispiele für die faktorenanalytische Bearbeitung von Klangsignalen (Spracherkennung), bei denen akustische Hauptfaktoren herausgezogen werden. Hiermit werden Sprachüberlagerungen (Flughafenansage, Konferenzmitschnitte) oder überlagerte Musikaufnahmen verständlicher gemacht (Blind Source Separation, Independent Component Analysis (ICA, siehe auch Weblinks).

Die typischen Anwendungen sind aber nach wie vor in der Psychologie und Soziologie. Zum Beispiel kann man aus einem Persönlichkeitstest, bei dem Probanden einen Fragebogen mit etwa 60 Fragen ausfüllen, 8 bis 12 Faktoren bestimmen und als Extraversion, Introversion, Großzügigkeit, Konventionalität usw. interpretieren.

Mathematischer Rahmen

Geometrische Bedeutung

Geometrisch gesehen, werden die in die Berechnung einbezogenen Items als Vektoren gesehen, die allesamt vom selben Ursprung ausgehen. Die Länge dieser p Vektoren wird durch die Kommunalität der jeweiligen Items und die Winkel zwischen den Vektoren werden durch deren Korrelation bestimmt. Die Korrelation r zweier Items x_i, x_j und der Winkel α zwischen deren Vektoren hängen folgendermaßen zusammen

r(x_i,x_j) = cosα

Eine Korrelation von 1 stellt also einen Winkel von 0°, eine Unkorreliertheit hingegen einen rechten Winkel dar. Ein Modell aus p Variablen spannt somit einen p-dimensionalen Raum auf. Ziel der Faktorenanalyse ist es, dieses Konstrukt geometrisch zu vereinfachen, also einen q-dimensionalen Unterraum zu finden. Es sollen durch das Extraktionsverfahren irrelevante Faktoren "ausgeblendet" werden. Die Lösung dieses Verfahrens sind sogenannte "Punktwolken" in einem q-dimensionalen Koordinatensystem. Die Koordinaten dieser Punkte stellen die sogenannten Faktorladungen dar. Durch ein Rotationsverfahren sollen die q extrahierten Faktoren so nahe wie möglich in diese Punktwolken gedreht werden.

Lineares Faktorenmodell

Der Faktorenanalyse liegt stets ein lineares Modell zugrunde:

x = μ + Γz + ε

mit

• x: Vektor der p zu erklärenden Variablen,
• μ: Vektor mit konstanten Werten,
• Γ: Matrix der „Faktorladungen“,
• z: Vektor der q Faktorwerte,
• ε: Zufallsvektor mit Mittelwert 0.

Es wird gefordert, dass die Komponenten von z zentriert, normiert und untereinander sowie mit ε unkorreliert sind.

In der Regel wird außerdem gefordert, dass die Komponenten von ε nicht miteinander korreliert sind. Wird diese Forderung fallengelassen, ist das Modell invariant unter orthogonaler Transformation der Γ, z und ε.

Das empirische Datenmaterial besteht aus n Realisationen des Variablenvektors x (z. B. Fragebögen mit p Fragen, die von n Probanden bearbeitet wurden). Zur Notationsvereinfachung kann angenommen werden, dass die Rohdaten in einem ersten Schritt der Auswertung zentriert wurden, so dass μ = 0.

Im Rahmen einer Faktorenanalyse sind zu schätzen:

• die Anzahl q der Faktoren,
• die $p\times q$ Faktorladungen aus Γ,
• die p Varianzen der Residuen aus ε,
• die 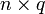$n\times q$ Realisationen des Faktorvektors z.

Die Schätzung erfolgt typischerweise in drei oder mehr Schritten:

• Es werden mögliche Faktoren identifiziert („extrahiert“);
• es wird entschieden, welche Anzahl q von Faktoren berücksichtigt werden soll;
• eventuell werden Faktoren rotiert, um ihre Interpretation zu vereinfachen;
• zuletzt werden die Faktorvektoren z für die einzelnen Realisationen von x (z. B. persönliche Werte für einzelne Probanden) geschätzt.

Hauptsatz

Aus den Modellannahmen folgt nach kurzer Rechnung der Hauptsatz der Faktoranalyse:

$\operatorname{Cov}(x_i,x_j) = (\Gamma\Gamma^\operatorname{T})_{ij} + \operatorname{Cov}(\epsilon_i,\epsilon_j).$

Für i = j vereinfacht sich dieser Satz zu

$\operatorname{Var}(x_i) = \sum_{k=1}^q{\Gamma_{ik}}^{\!\!2} + \operatorname{Var}(\epsilon_i).$

Hier steht Var für die Varianz, Cov für die Kovarianz und T für Matrixtransposition.

Der Term Var(ε_i) ist derjenige Anteil der Varianz der Observablen x_i, der durch das Faktorenmodell nicht erklärt wird. Der erklärte Anteil, Var(x_i) − Var(ε_i), also die Summe der quadrierten Faktorladungen, heißt Kommunalität der Variablen x_i.

Beispiel

In einer Müllsortierungsanlage seien zur Trennung des Mülls ein Magnet mit horizontaler Wirkungsrichtung und ein Gebläse mit vertikaler Wirkungsrichtung installiert. Die geometrischen Koordinaten der Müllstücke beim Niederfallen mögen Teil der erhobenen Daten sein. Man findet Richtungskorrelationen bei Stücken ohne Metall und großer Windanfälligkeit sowie bei Stücken mit Metallgehalt und geringer Windanfälligkeit.

Mit der Faktorenanalyse kann man dann zunächst finden, dass es zwei orthogonale Einflüsse gibt, die die Bewegungsrichtung beeinflussen.

Die Applikation der Untersuchungsmethode mag dann sein,

• zunächst die Anzahl der Faktoren zu schätzen (s.u.): Es ist sicher nicht interessant, für jedes einzelne Stück die Flugbahn zu dokumentieren und für jedes Stück einen eigenen Faktor anzunehmen, sondern aus den Korrelationen der Daten wesentliche gemeinsame Faktoren zu extrahieren: sehr wahrscheinlich bilden sich zwei Faktoren aus dem Datenmaterial heraus,

• die Stärke und die Orientierung dieser Einflüsse zu bestimmen (noch ohne Theorie über die Art der Einflüsse) oder

• aus der Kenntnis der Stückeigenschaften (metallisch, kompakt vs nichtmetallisch, windanfällig) die Faktoren inhaltlich zu beschreiben und für die kontinuierlichen Eigenschaften "Metallanteil" und "Windwiderstand" die "Ladungen" auf den Faktoren (deren Korrelationen mit der Magnetkraft und der Gebläsestärke) zu beschreiben.

Es wird an diesem Beispiel auch der Unterschied zwischen orthogonaler und schiefwinkliger Faktorenanalyse deutlich: vor allem in den Sozialwissenschaften gehen wir in der Regel von nicht-orthogonalen Faktoren aus: die sozialwissenschaftlichen Analoge zu Gebläse und Magnet im Beispiel müssen nicht unbedingt im Winkel von 90 Grad zueinander angeordnet sein und entsprechend einwirken.

In einer explorativen Situation, in der man noch keine Hypothesen über die Gründe für das Auftreten korrelierter Auftreffpunkte hat, wird man sich mit dem Auffinden und Markieren von zwei Faktoren zufrieden geben, und versuchen einzugrenzen, auf was diese Richtungskorrelationen zurückzuführen sind. In einer konfirmatorischen Situation wird man untersuchen, ob die aufgefundenen Korrelationen tatsächlich mit zwei Faktoren (wie vielleicht aus einer Theorie her anzunehmen) zu erklären sind, oder ob man einen dritten Faktor annehmen muss (oder tatsächlich nur ein Faktor wirkt).

Faktorenextraktion

Der erste Schritt der Faktorenanalyse, die Identifikation möglicher Faktoren, ist die Schätzung der Faktorladungen und der residuellen Varianzen. Für eine solche Schätzung benötigt man ein Gütekriterium. Diese essentielle theoretische Grundlage wird in weiten Teilen der Literatur nicht klar benannt.

Das "Gewicht" eines Faktors wird daraus bestimmt, wieviele Messvariablen mit ihm korrelieren, wie hoch sie "auf diesem Faktor laden". Quantifiziert wird dies durch die Summe der Ladungsquadrate. (Dies stimmt im orthogonalen Fall mit den Eigenwerten der Ladungsmatrix überein). Hierbei kann man die Faktoren nach der Höhe der Ladungsquadratsumme (LQS) sortieren.

Findet man gut separierbar zwei Gruppen von Faktoren, einer mit hoher LQS und ein weiterer mit niedriger LQS, wird man die Anzahl der Faktoren des Modells mit der Anzahl der LQS-hohen Faktoren gleichsetzen. Die Separierbarkeit dieser Gruppen kann man sich an einem Linien-Plot über die LQS ansehen; gibt es einen erkennbaren Knick, kann dieser als Trennungskriterium dienen (Scree-Test).

Ein anderes Kriterium ist, dass die LQS eines gemeinsamen Faktors größer als die Varianz einer einzelnen Messvariablen sein sollte (sonst wäre er schlecht als "gemeinsamer" Faktor zu verstehen). Dies meint dann i.d.R. LQS >= 1 (Kriterium nach Kaiser).

Faktoren- versus Hauptkomponentenanalyse

In der Hauptkomponentenanalyse wird ein p-dimensionaler Zufallsvektor x durch eine Linearkombination von Zufallsvektoren z_k dargestellt, die so gewählt werden, dass der erste Summand einen möglichst großen Anteil der Varianz von x erklärt, der zweite Summand möglichst viel von der verbleibenden Varianz, und so weiter. Wenn man diese Summe nach q Gliedern abbricht, erhält man als Darstellung von x

$x_i=\sum_{k=1}^q G_{ik} z_k + e_i$

mit dem Restterm

$e_i=\sum_{k=q+1}^p G'_{ik} z_k$.

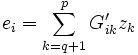Auf den ersten Blick sieht x wie das lineare Modell der Faktorenanalyse aus. Jedoch sind die Komponenten von e miteinander korreliert, da sie von denselben z_k abhängen. Deshalb erhält man aus einer Hauptkomponentenanalyse kein korrektes Faktorenmodell; man modelliert nur die Varianzen, nicht aber die Kovarianzen der x.^[1]

Maximum-Likelihood-Schätzung

Die Parameterschätzung steht auf einer sicheren Grundlage, wenn man die Γ, die ζ = Var(ε) und die (in den vorigen Abschnitten nicht mitnotierten) μ so bestimmt, dass sie die Likelihood L(x;μ,Γ,ζ) der beobachteten Realisationen von x maximieren.

Allerdings muss man bei diesem Schätzverfahren Annahmen über die Wahrscheinlichkeitsverteilung der manifesten Variablen x treffen, in der Regel also eine Normalverteilung annehmen.

Bestimmung der Faktorenzahl

Bei der Extraktion entstehen je nach Option und Verfahren sehr viele Faktoren. Nur wenige von ihnen erklären genug Varianz, um ihre weitere Verwendung rechtfertigen zu können. Die Auswahl der Faktoren dient in erster Linie der Gewinnung von aussagekräftigen, gut interpretierbaren Ergebnissen und ist damit nur eingeschränkt objektivierbar. Anhaltspunkte können folgende Kriterien liefern:

• Kaiser-Kriterium
• Scree-Test (auch Ellenbogenkriterium genannt)
• Parallelanalyse (eine Modifikation des Scree-Test)

Grundsätzlich sollten mehrere Kriterien herangezogen werden. Insbesondere im Zweifelsfall bietet es sich an, mehrere Faktorenzahlen durchzurechnen und im Hinblick auf Ladungen und Interpretierbarkeit zu überprüfen.

Gibt die der Untersuchung zugrundeliegende Theorie eine bestimmte Faktorenanzahl vor, kann diese auch in der Faktorenanalyse verwendet werden. Auch kann seitens des Untersuchenden mehr oder minder willkürlich festgelegt werden, welcher Anteil der Gesamtvarianz erklärt werden soll, die hierfür erforderliche Faktorenzahl leitet sich dann daraus ab. Jedoch ist auch bei einer theorie- oder varianzgeleiten Festlegung die Faktorenzahl anhand der genannten Kriterien auf Plausibilität zu prüfen.

Faktorrotation

Die Rotation soll Faktoren inhaltlich interpretierbar machen. Zur Verfügung stehen verschiedene Verfahren, darunter:

• Varimax (orthogonal)
• Oblimin (schiefwinklig)
• Quartimax (orthogonal)
• Equamax (orthogonal)
• Promax (schiefwinklig)

Diese Verfahren nähern sich der Rotationslösung iterativ an und erfordern meist zwischen 10 und 40 Iterationsrechnungen.

Grundlage für die Berechnung ist eine Korrelationsmatrix.

Siehe auch

• Kaiser-Meyer-Olkin-Kriterium (KMK oder KMO, auch measure of sampling adequacy, MSA)

Literatur

• Revenstorf, Dirk: Lehrbuch der Faktorenanalyse Kohlhammer, Stuttgart (1976)
• Überla, Karl:Faktorenanalyse , Springer Verlag, Berlin (1968)
• Mulaik, S.:The foundations of factor analysis McGraw-Hill, New York, (1972)
• Backhaus et. al: Multivariate Analysemethoden. 11. Auflage, Springer Verlag, Heidelberg (2005). S. 259-336
• Krzanowski, WJ: Principles of Multivariate Analysis. A User’s Perspective (rev. ed.). New York: Oxford University Press (2000).
• Steiger, JH: Factor indeterminacy in the 1930's and the 1970's. Some interesting parallels. Psychometrika 44, 157–167 (1979).

Weblinks

• Independent Component Analysis
• LernSTATS - Statistik Lernen mit dem Computer - Statistikkurs der Psychologie der FernUni-Hagen
• Anwendung der Faktorenanalyse im MPI für biologische Kybernetik, Tübingen (en, Video, ca 5min)

Einzelnachweise

1. ↑ Krzanowski, S. 482