Independent Component Analysis

Independent Component Analysis (ICA) löst das Blind-Source-Separation-Problem (BSS), indem angenommen wird, dass die Quellen einer Datenmischung statistisch unabhängig sind.

Problemstellung

Es wird dabei davon ausgegangen, dass ein Signal 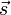$\vec{s}$ mit einer Mischmatrix A multipliziert wird. Das Resultat ist ein neues gemischtes Signal 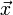$\vec{x}$ gleicher Dimension.

$\vec{x}=A\vec{s}$

Das Ziel der ICA ist es nun, wieder das Signal 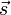$\vec{s}$ möglichst originalgetreu zu berechnen. Hierfür steht nur das Ergebnis der Mischung 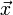$\vec{x}$ zur Verfügung und das Wissen, dass die Teilsignale ursprünglich stochastisch unabhängig waren. Es ist also eine geeignete Matrix A ^{− 1} gesucht, so dass

$\vec{s}=A^{-1}\vec{x}$.

Vorgehensweise

Wir gehen zunächst davon aus, dass unsere Daten von ihrem Mittelwert befreit sind.

Normierung der Varianz

Die Datenverteilung des gemischten Signals muss zunächst in ihrer Varianz normiert werden. Wir berechnen hierfür die Hauptkomponenten über die PCA. Als Ergebnis erhalten wir die Eigenwerte und die Eigenvektoren der Kovarianzmatrix des Signals. Der Satz von Eigenvektoren ergibt die Drehmatrix R, welche wir mit unserem Vektor 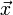$\vec{x}$ multiplizieren, so dass unsere Hauptkomponenten nun entlang der Achsen liegen. Die Eigenwerte e_i entsprechen der Varianz der jeweiligen Hauptkomponente. Wir bilden aus ihnen die Diagonalmatrix D:

$D = \begin{pmatrix} e_1^{-1} & & & 0 \\ & . & & \\ & & . & \\ 0 & & & e_n^{-1} \end{pmatrix}$

Durch das Multiplizieren mit der Diagonalmatrix führen wir ein sogenanntes Whitening durch und normieren die Varianz dabei auf 1.

$\vec{w}=DR\vec{x}$

Bestimmung der unabhängigen Komponenten

Nun wollen wir die Drehmatrix bestimmen, mit der unsere Daten stochastisch unabhängig werden. Dieser Schritt ist in einer Vielzahl von Ansätzen lösbar. Ziel ist es dabei jedoch immer die Nicht-Gaussheit zu maximieren oder die gemeinsame Information zu minimieren.

Kurtosis

Die Kurtosis ist ein Maß für die Abweichung von einer Normalverteilung. Sie ist definiert durch

kurt(X) = E(X⁴) − 3E(X²)² = E(X⁴) − 3.

Da unsere Daten in ihrer Varianz normiert sind, wird E(X²) gleich Eins. Unsere Kurtosis wird Null, wenn unsere Verteilung gaussähnlich ist. Ist die Kurtosis negativ, so ähnelt sie zunehmend einer Gleichverteilung. Ist sie positiv, so ist unsere Verteilung eher eine Laplace-Verteilung. Wir müssen also unsere Kurtosis maximieren bzw. minimieren, um uns von der Normalverteilung zu entfernen. Hierzu kann man das Gradientenverfahren verwenden, zum Beispiel in Anlehnung an die Lernregel von Oja.

Negentropie

Ein weiterer Ansatz ist die Maximierung der Negentropie.

$J(X) = H(X_{Gauss})-H(X) \geq 0$

Wobei X_Gauss in Hinsicht auf Varianz und Mittelwert der Verteilung von X entspricht. Da diese jedoch schwer zu bestimmen ist verwendet man hier meist eine Nährung.

Fast ICA

Fast ICA ist ein Fixpunktalgorithmus, welcher das Problem über ein Newtonverfahren löst.

Weblinks

• FastICA Implementierungen für Matlab, R, C++, und Python
• [1] (engl.) Was ist Independent Component Analysis?
• Swartz Center for Computational Neuroscience, University of California San Diego (ICA-basierte Analyse elektrophysiologischer Daten mit Hilfe der freien Matlab-Toolbox EEGLAB)