- Cantor'sches Diskontinuum
-
Unter der Cantor-Menge, auch cantorsches Diskontinuum, Cantor-Staub oder Wischmenge genannt, versteht man in der Mathematik eine gewisse Teilmenge der Menge der reellen Zahlen mit besonderen topologischen, maßtheoretischen, geometrischen und mengentheoretischen Eigenschaften: Sie ist
- kompakt, perfekt, total unzusammenhängend (ein „Diskontinuum“) und nirgends dicht;
- eine Lebesgue-Nullmenge;
- selbstähnlich und hat eine nichtganzzahlige Hausdorffdimension (ist also ein Fraktal);
- gleichmächtig zum Kontinuum (der Menge aller reellen Zahlen).
Sie ist nach dem deutschen Mathematiker Georg Cantor benannt.
Für eine Definition und genauere Beschreibungen dieser Menge siehe unten.
Allgemeiner nennt man auch gewisse Mengen oder topologische Räume Cantormengen, wenn sie einen Teil dieser Eigenschaften besitzen. Welche dieser Eigenschaften gefordert werden, hängt dabei vom mathematischen Gebiet und oft auch vom Kontext ab. In der Topologie wird ein topologischer Raum oder eine Teilmenge eines topologischen Raums Cantormenge genannt, wenn er/sie perfekt und total unzusammenhängend ist.
Inhaltsverzeichnis
Konstruktion
Die Cantor-Menge lässt sich mittels folgender Iteration konstruieren:
Man beginnt mit dem abgeschlossenen Intervall [0,1] der reellen Zahlen von 0 bis 1. Aus diesem Intervall wird das offene mittlere Drittel entfernt (weggewischt), also alle Zahlen, die strikt zwischen 1/3 und 2/3 liegen. Übrig bleiben die beiden Intervalle
![[0,\tfrac13]](/pictures/dewiki/98/bc78c0db5164629f786bacae8d82c66d.png) und
und ![[\tfrac23, 1]](/pictures/dewiki/53/5b8d71ab2b63027e8b3eee4f07d6353b.png) . Aus diesen beiden Intervallen wird wiederum jeweils das offene mittlere Drittel entfernt und man erhält nun vier Intervalle:
. Aus diesen beiden Intervallen wird wiederum jeweils das offene mittlere Drittel entfernt und man erhält nun vier Intervalle: ![[0,\tfrac19]](/pictures/dewiki/100/d6cbd5bf3298db07d887e0ad8ea181f5.png) ,
, ![[\tfrac29 ,\tfrac13 ]](/pictures/dewiki/101/e6296a3c0224393610c7bda766ed2221.png) ,
, ![[\tfrac23 ,\tfrac79 ]](/pictures/dewiki/53/5b85a5ab06b095b4c4342d403ae2fba0.png) und
und ![[\tfrac89 ,1]](/pictures/dewiki/101/e382e74cb0c84b73c1d98c8b46085f04.png) . Von diesen Intervallen werden wiederum die offenen mittleren Drittel entfernt. Dieser Schritt wird unendlich oft wiederholt.
. Von diesen Intervallen werden wiederum die offenen mittleren Drittel entfernt. Dieser Schritt wird unendlich oft wiederholt.Nach n Iterationen existieren 2n Intervalle, die insgesamt
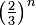 des ursprünglichen Intervalls abdecken. Je mehr Intervalle diese Menge enthält, desto geringer ist der Anteil am ursprünglichen Intervall.
des ursprünglichen Intervalls abdecken. Je mehr Intervalle diese Menge enthält, desto geringer ist der Anteil am ursprünglichen Intervall.Die Cantormenge besteht nun aus allen Punkten, die jedes Wegwischen überlebt haben.
Im Grenzfall ist der Anteil am ursprünglichen Intervall Null, obwohl unendlich viele Elemente vorliegen.
Die Hausdorff-Dimension und die Minkowski-Dimension der Cantormenge betragen
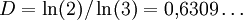
Dieses Konstruktionsverfahren ist verwandt mit dem für die Koch-Kurve.
Man kann die Cantormenge auch als die Menge aller Zahlen im Intervall [0,1] beschreiben, die eine Darstellung als Kommazahl zur Basis 3 besitzen, in der nur die Ziffern 0 und 2 vorkommen. Insbesondere enthält die Cantormenge mehr als nur die Randpunkte der entfernten Intervalle; diese Randpunkte sind genau die Zahlen in [0,1], welche sich mit einer 0-Periode oder mit einer 2-Periode schreiben lassen, zum Beispiel
ist der linke Randpunkt des im ersten Schritt entfernten Intervalls. Die Verwendung der Ziffer 1 wird durch die 2-Periode umgangen, welche dieselbe Zahl darstellt. (Dies ist nur für eine 1 direkt vor der 0-Periode möglich. An anderer Stelle kann aber keine 1 auftreten, da die Zahl sonst mitten in einem der gestrichenen Intervalle läge.) Darüber hinaus ist aber z.B. auch 1/4 in der Cantormenge, denn
0-1-Folgen
Das kartesische Produkt abzählbar unendlich vieler Kopien der zweielementigen Menge {0,1} ist die Menge aller unendlichen Folgen, die nur die Werte 0 und 1 annehmen, d.h. die Menge aller Funktionen
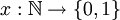 . Diese Menge wird mit
. Diese Menge wird mit 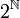 bezeichnet. Durch die oben genannte triadische Entwicklung lässt sich eine natürliche Bijektion zwischen der Cantormenge und der Menge
bezeichnet. Durch die oben genannte triadische Entwicklung lässt sich eine natürliche Bijektion zwischen der Cantormenge und der Menge 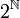 angeben: Die Zahl mit der triadischen Entwicklung
angeben: Die Zahl mit der triadischen Entwicklung 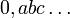 wird in die Folge
wird in die Folge 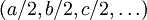 übersetzt; die Zahl 1/4 entspricht also der Folge
übersetzt; die Zahl 1/4 entspricht also der Folge 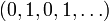 .
.Die Menge
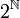 trägt auch eine natürliche Topologie (nämlich die Produkttopologie, die durch die diskrete Topologie auf der Menge {0,1} induziert wird); die gerade genannte Abbildung ist ein Homöomorphismus zwischen der Cantormenge und der Menge
trägt auch eine natürliche Topologie (nämlich die Produkttopologie, die durch die diskrete Topologie auf der Menge {0,1} induziert wird); die gerade genannte Abbildung ist ein Homöomorphismus zwischen der Cantormenge und der Menge 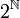 . Daher wird auch die Menge
. Daher wird auch die Menge 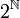 oft als „Cantormenge“ bezeichnet.
oft als „Cantormenge“ bezeichnet.Produktmaß und Cantorfunktion
Wenn man vom gleichverteilten Maß auf der Menge {0,1} ausgeht, erhält man auf der Menge
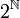 ein Produktmaß. Dieses Maß μ lässt sich so interpretieren: Man betrachtet ein Experiment, in dem unendlich oft eine faire Münze geworfen wird; Elemente von
ein Produktmaß. Dieses Maß μ lässt sich so interpretieren: Man betrachtet ein Experiment, in dem unendlich oft eine faire Münze geworfen wird; Elemente von 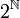 lassen sich als Ausgänge des Experiments interpretieren (die Folge
lassen sich als Ausgänge des Experiments interpretieren (die Folge 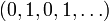 bedeutet zum Beispiel, dass immer abwechselnd Kopf und Zahl aufgetreten sind). Das Maß μ weist einer Teilmenge von
bedeutet zum Beispiel, dass immer abwechselnd Kopf und Zahl aufgetreten sind). Das Maß μ weist einer Teilmenge von 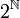 nun seine Wahrscheinlichkeit zu. Zum Beispiel besagt das starke Gesetz der großen Zahlen, dass die Menge G der „gleichverteilten“ Folgen Wahrscheinlichkeit 1 hat, wobei G die folgenden Menge ist:
nun seine Wahrscheinlichkeit zu. Zum Beispiel besagt das starke Gesetz der großen Zahlen, dass die Menge G der „gleichverteilten“ Folgen Wahrscheinlichkeit 1 hat, wobei G die folgenden Menge ist:Das oben genannte Maß μ lässt sich durch die oben genannte Bijektion in ein Wahrscheinlichkeitsmaß μ auf der Cantormenge übersetzen. (Eine alternative Beschreibung von μ ergibt sich als Hausdorffmaß zur Dimension ln2 / ln3.)
Dieses Maß μ ist ein Beispiel für ein Maß, dessen Verteilungsfunktion zwar stetig, aber nicht absolut stetig ist. Die Verteilungsfunktion
heißt auch „cantorsche Treppenfunktion“. Auf jedem Intervall im Komplement der Cantormenge ist diese Funktion konstant; auf dem Intervall
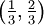 hat sie zum Beispiel den Wert 1/2, und auf dem Intervall
hat sie zum Beispiel den Wert 1/2, und auf dem Intervall 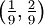 hat sie den Wert 1/4.
hat sie den Wert 1/4.Die cantorsche Treppenfunktion ist also fast überall differenzierbar mit Ableitung 0, aber dennoch nicht konstant.
Andere Cantormengen
Die Cantormenge (auch Mitteldrittel-Cantormenge, middle thirds Cantor set) wurde oben beschrieben. Unter einer Cantormenge versteht man eine Menge von reellen Zahlen, die man mit einer Variante des obigen Wischprozesses bekommt, wobei man nun die Längen und Anzahlen der weggewischten Intervalle variieren kann:
Man beginnt mit einem beliebigen Intervall [a,b] von reellen Zahlen. Im ersten Schritt entfernt man endlich viele offene disjunkte Unterintervalle (mindestens aber eines) und erhält so endlich viele abgeschlossene Intervalle (mindestens 2).
Im zweiten Schritt entfernt man aus jedem der enthaltenen Intervalle wiederum endlich viele Unterintervalle (jeweils mindestens eines).
Wiederum definiert dieser Prozess eine Menge von reellen Zahlen, nämlich jene Punkte, die niemals in eines der weggewischten Intervalle gefallen sind.
Man kann zeigen, dass alle so konstruierten Cantormengen zueinander homöomorph sind und dass sie insbesondere zur Menge aller reellen Zahlen gleichmächtig sind. Indem man die Proportion „Längen der weggewischten Intervalle: Längen der übrigbleibenden Intervalle“ geeignet variiert, kann man eine Cantormenge erzeugen, deren Hausdorff-Dimension eine beliebige vorgegebene Zahl im Intervall [0,1] ist.
Ein zweidimensionales Analogon der Cantor-Menge ist der Sierpinski-Teppich, ein dreidimensionales der Menger-Schwamm.
Wikimedia Foundation.


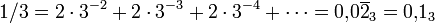
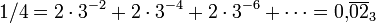
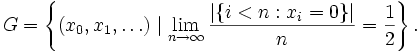
![\begin{align}
F_{\mu'} : [0,1]&\to [0,1]\\
x &\mapsto \mu'([0,x] \cap C)
\end{align}](/pictures/dewiki/101/e9d28d5f8fa60bf8ccdd8cd9bf67ca53.png)