Hausdorffeigenschaft

Hausdorff-Raum (T2)

berührt die Spezialgebiete

Mathematik Topologie

ist Spezialfall von

topologischer Raum präregulärer Raum (R1) Kolmogoroff-Raum (T0)

umfasst als Spezialfälle

Urysohn-Raum (T2½) Tychonoff-Raum (T3½) normaler Hausdorff-Raum (T4)

Beispiele sind

metrischer Raum ganze Zahlen Z

Ein Hausdorff-Raum (nach Felix Hausdorff) oder separierter Raum ist ein topologischer Raum M, in dem das folgende Trennungsaxiom T₂ (auch Hausdorffeigenschaft oder Hausdorff'sches Trennungsaxiom genannt) gilt:

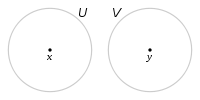
Für alle x,y aus M mit x≠y existieren disjunkte offene Umgebungen U(x) und V(y).

Mit anderen Worten: alle paarweise verschiedenen Punkte x und y aus M werden durch Umgebungen getrennt.

Einordnung in die Hierarchie topologischer Räume

Ein Hausdorff-Raum ist präregulär (R₁):

alle paarweise topologisch unterscheidbaren Punkte x und y aus M werden durch Umgebungen getrennt,

und hat die Kolmogoroff-Eigenschaft (T₀):

alle paarweise verschiedenen Punkte x und y aus M sind topologisch unterscheidbar.

Topologisch unterscheidbar heißen zwei Punkte x und y genau dann, wenn es eine offene Menge gibt, die den einen Punkt enthält, den anderen aber nicht.

Beweis:

• Wenn R₁ und T₀ gegeben sind, folgt unmittelbar T₂: diesen Schluss kann man rein formal ziehen, ohne zu wissen, was topologisch unterscheidbar überhaupt heißt.
• Der umgekehrte Schluss von T₂ auf R₁ und T₀ geht so:
  • Aus der Definition von T₂ folgt für verschiedene x, y die Existenz der Menge U(x), die x, aber nicht y enthält, ergo gilt T₀.
  • Seien x, y zwei topologisch unterscheidbare Punkte: dann gibt es eine Menge, die den einen Punkt enthält, den anderen aber nicht; somit ist x≠y. Dann folgt mit T₂, dass x und y durch Umgebungen getrennt sind. Ergo gilt R₁.

Spezialisierung

Ein Hausdorff-Raum, der zusätzlich noch normal ist, wird als T₄-Raum bezeichnet.

Beispiele

Insbesondere sind in topologischen Hausdorff-Räumen Grenzwerte - anders als in allgemeinen topologischen Räumen - eindeutig.

So gut wie alle in der Analysis betrachteten Räume sind Hausdorff-Räume. Insbesondere ist jeder metrische Raum ein Hausdorff-Raum.

Ein Beispiel für einen Hausdorff-Raum, der kein metrischer Raum ist, ist die Menge der abzählbaren Ordinalzahlen mit der gewöhnlichen Ordnungstopologie.

Wird das Spektrum eines Ringes mit der Zariski-Topologie versehen, erhält man einen nüchternen topologischen Raum, der meist nicht präregulär, geschweige denn hausdorffsch ist.

Literatur

• B. v. Querenburg: Mengentheoretische Topologie, Springer, Berlin 2001, ISBN 3540677909