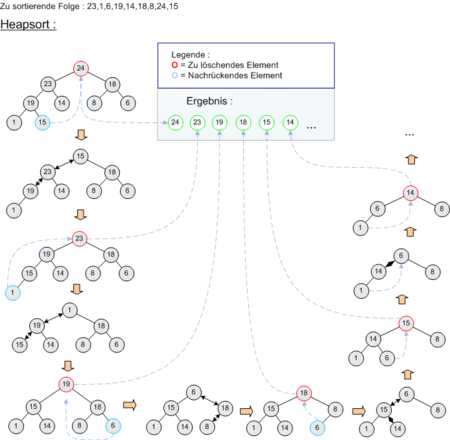
- Heap Sort
-
Heapsort oder Haldensortierung ist ein 1964 von Robert W. Floyd und J. W. J. Williams entwickeltes, relativ schnelles Sortierverfahren. Es handelt sich um eine Verbesserung von Selectionsort. Seine Komplexität ist bei einem Array der Länge n in der Landau-Notation ausgedrückt O(n·log(n)). Heapsort arbeitet zwar in-place (auch: in situ), ist jedoch nicht stabil.
Inhaltsverzeichnis
Heaps
Die Voraussetzung dafür, dass man ein Array von sortierbaren Werten mit Heapsort sortieren kann, ist, dass dieses einen binären Heap (auch "Halde" oder "Haufen") repräsentiert. Ist dies nicht der Fall, so muss man es zuerst in einen Heap überführen.
Man beachte, dass für die zweite Hälfte jedes Arrays die Heap-Eigenschaft bereits erfüllt ist, denn jeder Knoten in der zweiten Hälfte des Arrays entspricht im Heap einem Blatt, hat also keinen Nachfolgeknoten, dessen Wert größer sein könnte als der eigene (im Folgenden wird der Einfachheit halber der Knoten mit dem größten Wert der „größte Knoten“ genannt).
Um ein Array in einen Heap zu überführen, beginnt man deshalb in der Mitte des Arrays. Man „versickert“ nun sukzessive alle davor liegenden Knoten, bis das erste Element versickert wurde. Versickern (auch: absinken) heißt, dass man einen Knoten mit dem größeren seiner beiden Nachfolgeknoten vertauscht, falls dieser größer ist als er selbst, und damit so lange fortfährt, bis er keinen Nachfolgeknoten mehr hat, der größer ist als er selbst.
Um die Rechnung zu vereinfachen, wird im Folgenden vorausgesetzt, dass das erste Element des Arrays den Index 1 hat. Die Nachfolger eines Knotens mit dem Index
iliegen dann an den Positionen2·iund2·i+1.Beispiel für die Überführung in einen Max-Heap
Man möchte ein Array mit dem Inhalt
[H|E|A|P|S|O|R|T]in einen Max-Heap überführen, wobei gilt: A<B<C<…<Y<Z.1 2 3 4 5 6 7 8 H|E A|P S O R|T Wir beginnen links von der Mitte, d. h. bei P: | |^ |^ sein Nachfolger ist T. Da T>P ist, tauschen wir beide. H|E A|T S O R|P Wir fahren mit dem A fort. Seine Nachfolger sind | ^| ^ ^| O und R. Es gilt sowohl O>A als auch R>A. | | | R>O, also tauschen wir R und A. H|E R|T S O A|P Dann vergleichen wir E mit seinen Nachfolgern T und S. |^ |^ ^ | Es gilt T>S und T>E. Deshalb müssen wir T und E vertauschen. H|T R|E S O A|P Wir müssen nun E weiter versickern, denn der neue | |^ |^ Nachfolger von E ist P, und P>E. H|T R|P S O A|E Nun vergleichen wir H mit seinen ^|^ ^| | Nachfolgern T und R. T>R und T>H. T|H R|P S O A|E Wir versickern das H weiter. |^ |^ ^ | S>P und S>H. T|S R|P H O A|E Wir haben das Array nun in einen Max-Heap überführt. (Hilfslinien deuten die Baumebenen an.)
Prinzip der Sortierung (Max-Heap)
Der eigentliche Sortieralgorithmus nutzt die Tatsache aus, dass die Wurzel eines Heaps stets der größte Knoten ist. Da im fertig sortierten Array der größte Wert ganz rechts stehen soll, vertauscht man das erste mit dem letzten Arrayelement. Das Element am Ende des Arrays ist nun an der gewünschten Position und bleibt dort. Den Rest des Arrays muss man wieder in einen Max-Heap überführen, indem man das erste Element versickert. Anschließend vertauscht man das erste mit dem vorletzten Element, d. h. die beiden größten Werte sind wie gewünscht am Ende des Arrays. Man versickert das nun erste Element, usw.
Beispiel für Heapsort mit Zahlen
Beispiel für Heapsort mit Buchstaben
Ein weiteres Beispiel mit Buchstaben : Wir sortieren den oben erhaltenen Heap
[T|S|R|P|H|O|A|E].1 2 3 4 5 6 7 8 T S R P H O A E Wir vertauschen das erste Element mit dem letzten. ^ ^ E S R P H O A|T Das T ist nun an der korrekten Position. ^ ^ ^ Nun müssen wir das E versickern. E<S und S<R S E R P H O A|T P>H und P>E. ^ ^ ^ S P R E H O A|T Wir versickern E nicht weiter, denn T liegt bereits ^ ^ jenseits des Heaps im fertig sortierten Bereich. Wir haben also wieder einen korrekten Heap und können S und A vertauschen, womit auch das S sortiert ist. A P R E H O|S T Jetzt müssen wir das A versickern. ^ ^ ^ R>P und R>A. R P A E H O|S T Da das S bereits korrekt liegt, vergleichen wir ^ ^ nur A und O. O>A. R P O E H A|S T Die Heap-Eigenschaft für das linke Teilarray ist wieder ^ ^ erfüllt. Wir vertauschen R und A. A P O E H|R S T Wir versickern A. ^ ^ ^ P>O und P>A. P A O E H|R S T Wir versickern A weiter. H>E und H>A. ^ ^ ^ P H O E A|R S T Wir vertauschen P und A. ^ ^ A H O E|P R S T Wir versickern A. ^ ^ ^ O>H und O>A. O H A E|P R S T Wir vertauschen O und E. ^ ^ E H A|O P R S T Wir versickern E. ^ ^ ^ H>A und H>E. H E A|O P R S T Wir vertauschen H und A. ^ ^ A E|H O P R S T Wir versickern A. E>A. ^ ^ E A|H O P R S T Wir vertauschen E und A. ^ ^ A|E H O P R S T Das Array ist jetzt fertig sortiert.
Implementierung
C++
#include <iterator> template< typename Iterator > void adjust_heap( Iterator first , typename std::iterator_traits< Iterator >::difference_type current , typename std::iterator_traits< Iterator >::difference_type size , typename std::iterator_traits< Iterator >::value_type tmp ) { typedef typename std::iterator_traits< Iterator >::difference_type diff_t; diff_t top = current, next = 2 * current + 2; for ( ; next < size; current = next, next = 2 * next + 2 ) { if ( *(first + next) < *(first + next - 1) ) --next; *(first + current) = *(first + next); } if ( next == size ) *(first + current) = *(first + size - 1), current = size - 1; for ( next = (current - 1) / 2; top < current && *(first + next) < tmp; current = next, next = (current - 1) / 2 ) { *(first + current) = *(first + next); } *(first + current) = tmp; } template< typename Iterator > void pop_heap( Iterator first, Iterator last) { typedef typename std::iterator_traits< Iterator >::value_type value_t; value_t tmp = *--last; *last = *first; adjust_heap( first, 0, last - first, tmp ); } template< typename Iterator > void heap_sort( Iterator first, Iterator last ) { typedef typename std::iterator_traits< Iterator >::difference_type diff_t; for ( diff_t current = (last - first) / 2 - 1; current >= 0; --current ) adjust_heap( first, current, last - first, *(first + current) ); while ( first < last ) pop_heap( first, last-- ); }
Java
/** * sortiert ein Array mit heapsort * @param a das array */ private static void heapSort(int[] a) { generateMaxHeap(a); //hier wird sortiert for(int i = a.length -1 ; i > 0 ; i--) { vertausche(a, i, 0); versenke(a, 0,i); } } /** * Erstellt einen MaxHeap Baum im Array * @param a das array */ private static void generateMaxHeap(int[] a) { //starte von der Mitte rückwärts. for(int i = (a.length / 2) - 1; i >= 0 ; i--) { versenke(a,i,a.length); } } /** * versenkt ein element im baum * @param a Das Array * @param i Das zu versenkende Element * @param n Die letzte Stelle im Baum die beachtet werden soll */ private static void versenke(int[] a, int i,int n) { while(i <= (n / 2) - 1) { int kindIndex = ((i+1) * 2) - 1; // berechnet den Index des linken kind //bestimme ob ein rechtes Kind existiert if(kindIndex + 1 <= n -1) { //rechtes kind existiert if(a[kindIndex] < a[kindIndex+1]) { kindIndex++; // wenn rechtes kind größer ist nimm das } } //teste ob element sinken muss if(a[i] < a[kindIndex]) { vertausche(a,i,kindIndex); //element versenken i = kindIndex; // wiederhole den vorgang mit der neuen position } else break; } } /** * Vertauscht die arraypositionen von i und kindIndex * @param a Das Array in dem getauscht wird * @param i der erste index * @param kindIndex der 2. index */ private static void vertausche(int[] a, int i, int kindIndex) { int z = a[i]; a[i] = a[kindIndex]; a[kindIndex] = z; }
Pascal
const SIZE = 20000; type TFeld = array[1..SIZE] of integer; procedure heapsort(var f:TFeld); procedure genheap(var f:TFeld); { Heap (mit linearem Aufwand) aufbauen } var i,j,max,temp:integer; begin for i := SIZE div 2 downto 2 do begin { zweite Hälfte des Feldes braucht nicht betrachtet werden } j:=i; while j <= SIZE div 2 do begin max := j * 2 + 1; { finde Maximum der (beiden) Söhne } if max > SIZE then dec(max) else if f[max-1] > f[max] then dec(max); if f[j] < f[max] then begin { ggf. tauschen } temp := f[j]; f[j] := f[max]; f[max] := temp; end; j := max; end; end; end; function popmax(var f:TFeld;heapsize:integer):integer; var i,max,temp:integer; begin popmax := f[1]; f[1] := f[heapsize]; i := 1; while i <= (heapsize div 2) do begin { letztes Element an Anfang setzen und versickern lassen } max := i * 2 + 1; { finde Maximum der (beiden) Söhne } if max > heapsize then dec(max) else if f[max-1] > f[max] then dec(max); if f[i] < f[max] then begin { ggf. tauschen } temp := f[i]; f[i] := f[max]; f[max] := temp; end; i := max; end; end; var i:integer; begin genheap(f); for i:=SIZE downto 1 do f[i] := popmax(f,i); end;
Laufzeit
Man kann zeigen, dass der Aufbau des Heaps, in Landau-Notation ausgedrückt, in
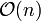 Schritten ablaufen kann. In einem großen, zufällig verteilten Datenfeld (100 bis 10^10 Datenelemente) sind durchschnittlich mehr als 4 aber weniger als 5 signifikante Sortieroperationen pro Element nötig (2,5 Datenvergleiche und 2,5 Zuweisungen). Dies liegt daran, dass ein zufälliges Element mit exponentiell zunehmender Wahrscheinlichkeit einen geeigneten Vaterknoten findet (60%, 85%, 93%, 97%, ...). Den Worst Case stellen mit
Schritten ablaufen kann. In einem großen, zufällig verteilten Datenfeld (100 bis 10^10 Datenelemente) sind durchschnittlich mehr als 4 aber weniger als 5 signifikante Sortieroperationen pro Element nötig (2,5 Datenvergleiche und 2,5 Zuweisungen). Dies liegt daran, dass ein zufälliges Element mit exponentiell zunehmender Wahrscheinlichkeit einen geeigneten Vaterknoten findet (60%, 85%, 93%, 97%, ...). Den Worst Case stellen mit  weitgehend vorsortierte Daten dar, weil der Heapaufbau de facto eine schrittweise vollständige Invertierung der Sortierreihenfolge darstellt. Der günstigste, aber unwahrscheinliche, Fall ist ein bereits umgekehrt sortiertes Datenfeld (1 Vergleich pro Element, keine Zuweisung). Gleiches gilt, wenn fast alle Daten identisch sind.
weitgehend vorsortierte Daten dar, weil der Heapaufbau de facto eine schrittweise vollständige Invertierung der Sortierreihenfolge darstellt. Der günstigste, aber unwahrscheinliche, Fall ist ein bereits umgekehrt sortiertes Datenfeld (1 Vergleich pro Element, keine Zuweisung). Gleiches gilt, wenn fast alle Daten identisch sind.Das Versickern eines Elements von der Wurzel her benötigt im ungünstigsten Fall (Worst Case)
 Schritte. Dies ist bei exakt inverser Reihenfolge der Fall. Durchschnittlicher und ungünstigster Fall unterscheiden sich jedoch praktisch nur unwesentlich:
Schritte. Dies ist bei exakt inverser Reihenfolge der Fall. Durchschnittlicher und ungünstigster Fall unterscheiden sich jedoch praktisch nur unwesentlich: 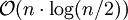 zu
zu  . Günstig ist nur ein Feld, dessen Elemente fast alle den gleichen Wert haben. Sind aber nur weniger als ca. 80% der Daten identisch, dann entspricht die Laufzeit bereits dem durchschnittlichen Fall. Eine vorteilhafte Anordnung von Daten mit mehreren verschiedenen Werten ist prinzipbedingt unmöglich, da dies der Heapcharakteristik widerspricht.
. Günstig ist nur ein Feld, dessen Elemente fast alle den gleichen Wert haben. Sind aber nur weniger als ca. 80% der Daten identisch, dann entspricht die Laufzeit bereits dem durchschnittlichen Fall. Eine vorteilhafte Anordnung von Daten mit mehreren verschiedenen Werten ist prinzipbedingt unmöglich, da dies der Heapcharakteristik widerspricht.Auf heterogenen Daten - vorsortiert oder nicht - dominiert das Versickern mit wenigstens über 60% der Zeit, meistens über 80%. Somit garantiert Heapsort eine Gesamtlaufzeit von
 . Auch im besten Fall wird eine Laufzeit von
. Auch im besten Fall wird eine Laufzeit von  benötigt.[1][2]
benötigt.[1][2]Im Durchschnitt ist Heapsort nur dann schneller als Quicksort, wenn Vergleiche auf den zu sortierenden Daten sehr aufwendig sind und gleichzeitig eine für Quicksort ungünstige Datenanordnung besteht (z.B. viele gleiche Elemente). In der Praxis ist bei unsortierten oder teilweise vorsortierten Daten Quicksort oder Introsort um einen konstanten Faktor (2 bis 5) schneller als Heapsort. Allerdings spricht das Worst-Case-Verhalten von
 gegenüber
gegenüber 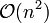 bei Quicksort für Heapsort. Introsort ist degegen in fast allen Fällen schneller als Heapsort, lediglich in entarteten Fällen 20 % bis 30 % langsamer.
bei Quicksort für Heapsort. Introsort ist degegen in fast allen Fällen schneller als Heapsort, lediglich in entarteten Fällen 20 % bis 30 % langsamer.Varianten
Bottom-Up-Heapsort
Die wichtigste Variante des Heapsort-Algorithmus ist das Bottom-Up-Heapsort, das häufig fast die Hälfte der nötigen Vergleichsoperationen einsparen kann und sich folglich besonders da rentiert, wo Vergleiche aufwändig sind. (Siehe dort auch die wissenschaftlich entscheidenden Referenzen zu Heapsort.)
Smoothsort
Normales Heapsort sortiert bereits weitgehend vorsortierte Felder nicht schneller als andere. Die größten Elemente müssen immer erst ganz nach vorn an die Spitze des Heaps wandern, bevor sie wieder nach hinten kopiert werden. Smoothsort ändert das, indem es im Prinzip die Reihenfolge des Heaps umdreht. Dabei ist allerdings beträchtlicher Aufwand nötig, um den Heapstatus beim Sortieren aufrecht zu erhalten.
Ternäre Heaps
Eine andere Optimierung verwendet statt binären ternäre Heaps. Diese Heaps beruhen statt auf Binärbäumen auf Bäumen, bei denen jeder vollständig besetzte Knoten 3 Kinder hat. Damit kann die Zahl der Vergleichsoperationen um etwa 3–4 % reduziert werden (bei einigen Tausend bis einigen Millionen Elementen). Außerdem sinkt der sonstige Aufwand deutlich; insbesondere müssen durch den flacheren Heap knapp ein Drittel weniger Elemente beim Versickern verschoben werden.
In einem binären Heap kann ein Element mit 2n Vergleichen um n Ebenen abgesenkt werden und hat dabei durchschnittlich 3/2·(2n-1) Indizes übersprungen. In einem ternären Heap kann ein Element mit 3m Vergleichen um m Ebenen abgesenkt werden und hat dabei durchschnittlich 3m-1 Indizes übersprungen. Wenn bei gleicher Reichweite der relative Aufwand x := 3m/2n ist, dann gilt
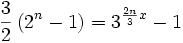 , also
, also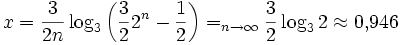
Bei n=18 (realistisch bei knapp 1 Million Elementen) ergibt sich 0,977; die 1 wird oberhalb von n=10 unterschritten. In der Praxis ist die Ersparnis etwas größer, u.a. deswegen, weil ternäre Bäume mehr Blätter haben und deshalb beim Aufbau des Heaps weniger Elemente versickert werden müssen.
Insgesamt kann die Sortierung mit ternären Heaps bei großen Feldern (mehrere Millionen Elemente) und einfacher Vergleichsoperation 20–30 % Zeit einsparen. Bei kleinen Feldern (bis etwa tausend Elemente) lohnen sich ternäre Heaps nicht oder sind sogar langsamer.
n-äre Heaps
Bei noch breiteren Bäumen bzw. flacheren Heaps steigt die Zahl der nötigen Vergleichsoperationen wieder an. Trotzdem können sie vorteilhaft sein, weil der sonstige Aufwand (vor allem der für das Kopieren von Elementen) weiter sinkt und geordneter auf die Elemente zugegriffen wird, was die Effizienz von Caches erhöhen kann. Sofern bei großen Feldern nur ein einfacher numerischer Vergleich durchzuführen ist und Schreiboperationen relativ langsam sind, können 8 oder mehr Kinder pro Knoten optimal sein.
Einfache Beispielsimplementierung mit Heaps beliebiger Arität (ab 2) in C99:
int heapsort( int * data, int n ) // zu sortierendes Feld und seine Länge { const int WIDTH= 8; // Anzahl der Kinder pro Knoten int val, parent, child, w, max, i; int m= (n + (WIDTH - 2)) / WIDTH; // erstes Blatt im Baum int count= 0; // Zähler für Anzahl der Vergleiche while ( 1 ) { if ( m ) { // Teil 1: Konstruktion des Heaps parent= --m; val= data[parent]; // zu versickernder Wert } else if ( --n ) { // Teil 2: eigentliche Sortierung val= data[n]; // zu versickernder Wert vom Heap-Ende data[n]= data[0]; // Spitze des Heaps hinter den Heap in parent= 0; // den sortierten Bereich verschieben } else // Heap ist leer; Sortierung beendet break; while ( (child= parent * WIDTH + 1) < n ) // erstes Kind; { // Abbruch am Ende des Heaps w= n - child < WIDTH ? n - child : WIDTH; // Anzahl der vorhandenen Geschwister count += w; for ( max= 0, i= 1; i < w; ++i ) // größtes Kind suchen if ( data[child+i] > data[child+max] ) max= i; child += max; if ( data[child] <= val ) // kein Kind mehr größer als der break; // zu versickernde Wert data[parent]= data[child]; // größtes Kind nach oben rücken parent= child; // in der Ebene darunter weitersuchen } data[parent]= val; // versickerten Wert eintragen } return count; }
Zu Vergleichszwecken gibt die Funktion die Anzahl der durchgeführten Vergleiche zurück.
Siehe auch
Einzelnachweise
- ↑ Russel Schaffer, Robert Sedgewick: The analysis of heapsort. In: Journal of Algorithms, Volume 15, Issue 1. Juli 1993. S. 76–100, ISSN 0196-6774
- ↑ Bela Bollobas, Trevor I. Fenner, Alan M. Frieze: On the best case of heapsort. In: Journal of Algorithms, Volume 20, Issue 2. März 1996. S. 205–217. ISSN 0196-6774
Weblinks
- Video zur Visualisierung von Heap Sort
- Robert F. Stärk: Animated Sorting Algorithms (Java-Beispiele)
- VisuSort Framework - Visualisierung diverser Sortieralgorithmen (Windows)
- Sortierung - Algorithmen und Visualisierung
- Java-Applet zur Demonstration
- Weiteres Java-Applet
- Heapsort-Code
- Heapsort Java-Applet mit Visualisierung der Einzelschritte und Quellcode
Wikimedia Foundation.