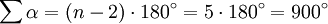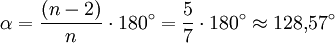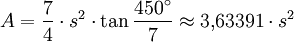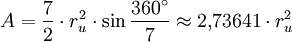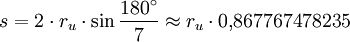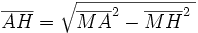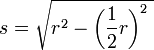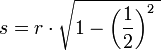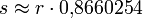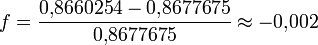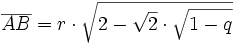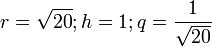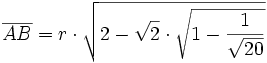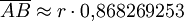- Heptagon
-
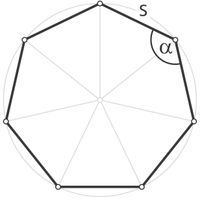
Ein regelmäßiges Siebeneck Das Siebeneck (griech. heptagon von hepta = sieben) ist eine geometrische Figur. Es gehört zur Gruppe der Vielecke (Polygone). Es ist definiert durch sieben Punkte. Sofern nichts anderes gesagt wird, ist von einem ebenen, regelmäßigen Siebeneck die Rede (siehe Bild), dessen sieben Seiten gleich lang sind und dessen sieben Eckpunkte auf einem gemeinsamen Umkreis liegen.
Inhaltsverzeichnis
Mathematische Zusammenhänge
Formel für Winkelberechnungen
Die Summe der Innenwinkel des Siebenecks beträgt stets 900° und ergibt sich aus einer allgemeinen Formel für Polygone, in der für die Variable n die Anzahl der Eckpunkte des Polygons eingesetzt werden muss (in diesem Fall: n = 7):
Der Winkel, den zwei benachbarte Seitenkanten im ebenen, regelmäßigen Siebeneck miteinander einschließen, beträgt (wiederum nach einer allgemeinen Formel für regelmäßige Polygone):
Formel für die Fläche A
Ein Siebeneck besitzt einen eindeutig bestimmbaren Flächeninhalt, welcher sich stets durch Zerlegen in Dreiecke berechnen lässt. Die Fläche des regelmäßigen Siebenecks beträgt das Siebenfache der Fläche eines jener Dreiecke, die von seinem Mittelpunkt und je zwei benachbarten Eckpunkten aufgespannt werden.
oder mit dem Umkreisradius:
Formel für die Seitenlänge s
Näherungskonstruktionen
Ein regelmäßiges Siebeneck kann nicht mit Zirkel und Lineal exakt konstruiert werden.
Nach einem Beweis von Carl Friedrich Gauß sind, wenn n eine Primzahl ist, die und nur die n-Ecke konstruierbar, bei denen es natürliche Zahlen k gibt, so dass n eine Primzahl der Gestalt
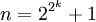 ist. Das sind
ist. Das sind 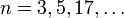 für
für 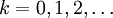 Darunter befindet sich also nicht n = 7. Deshalb kann eine Konstruktion für das regelmäßige Siebeneck nicht existieren.[1]
Darunter befindet sich also nicht n = 7. Deshalb kann eine Konstruktion für das regelmäßige Siebeneck nicht existieren.[1]Es gibt jedoch für die Praxis einige ausreichend genaue Näherungskonstruktionen.
Es geht darum, eine Strecke zu erhalten, welche möglichst genau das 0,86776747823-fache eines gegebenen Radius ist.
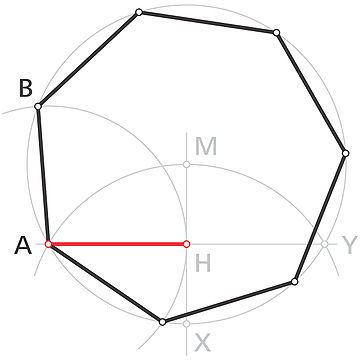
Eine sehr einfache Näherungskonstruktion ist in folgender Zeichnung dargestellt:
- Vom Mittelpunkt des Umkreises zeichnet man eine Gerade, die den Umkreis im Punkt X schneidet.
- Dann zeichnet man einen Kreis um X, der durch M verläuft und den Umkreis in den Punkten A und Y schneidet.
- Die Gerade AY schneidet die Strecke
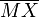 im Halbierungspunkt H.
im Halbierungspunkt H. - Die rote Strecke
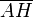 ist eine gute Näherung für die Seitenlänge des Siebenecks.
ist eine gute Näherung für die Seitenlänge des Siebenecks. - Die Eckpunkte B bis G erhält man durch Abschlagen der Strecke
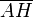 .
.
Genau dieselbe Streckenlänge lässt sich folgendermaßen konstruieren:
- Konstruiere das dem Umkreis einbeschriebene regelmäßige (gleichseitige) Dreieck.
- Die Hälfte einer Dreiecksseite nimm als Näherung für die Seite des Siebenecks.
In dieser Form war sie bereits dem im 10. Jahrhundert in Bagdad wirkenden Gelehrten Abu l-Wafa bekannt.[2]
Aus dem rechtwinkligen Dreieck AHM errechnet sich:
Mit
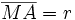 ;
; 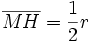 und
und 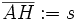
Bei dieser Konstruktion beträgt der Fehler
Die mit dieser Konstruktion gewonnene Seitenlänge ist etwas zu kurz und beträgt 99,8 Prozent des wahren Wertes. Oder anders formuliert: Ab einem Umkreisradius von ungefähr 57,4 cm beträgt der Fehler in der Seitenlänge mehr als einen Millimeter.
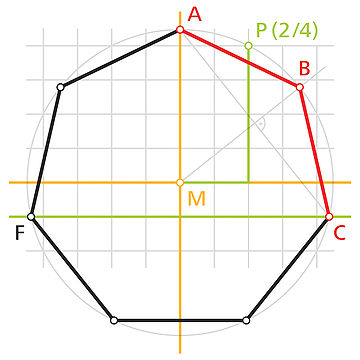
Eine etwas aufwändigere aber verblüffend genaue Näherungskonstruktion ist in folgender Zeichnung dargestellt:
- In einem rechtwinkeligen Koordinatensystem zeichnet man einen Kreis, der seinen Mittelpunkt im Ursprung (0 / 0) hat und genau durch den Punkt P mit den Koordinaten (2 / 4) verläuft.
- Der Schnittpunkt der positiven y-Achse mit der Kreislinie wird als Eckpunkt A des regelmäßigen Siebenecks festgelegt.
- Die Gerade y = − 1 (horizontale grüne Linie) schneidet die Kreislinie in unmittelbarer Nähe der Eckpunkte C und F.
- Wenn man die Streckensymmetrale der Strecke AC mit dem Kreis schneidet, erhält man eine Näherung für den Eckpunkt B.
- Die rote Strecke
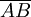 oder
oder 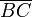 ist eine sehr gute Näherung für die Seitenlänge des regelmäßigen Siebenecks.
ist eine sehr gute Näherung für die Seitenlänge des regelmäßigen Siebenecks. - Die Eckpunkte D, E und G erhält man durch Spiegelung oder Abschlagen der Seitenlänge am Umkreis.
Bezeichnet man den Umkreisradius mit r, den Abstand der
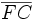 von M mit h, und substituiert
von M mit h, und substituiert 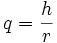 so ergibt sich bei dieser Konstruktion:
so ergibt sich bei dieser Konstruktion:und mit den Werten
ergibt sich:
Die mit dieser Konstruktion gewonnene Seitenlänge ist also etwas zu lang und der Fehler beträgt näherungsweise 0,00057821133, also 0,0578 Prozent. Oder anders formuliert: Bei einem Umkreisradius von ungefähr 199,3 cm beträgt der Fehler in der Seitenlänge einen Millimeter.
Verwendung des Siebenecks in der Praxis
Das 20-Eurocent-Stück hat sieben Einkerbungen, um Blinden die Unterscheidung von anderen Münzen zu erleichtern (Spanische Blume). Die alte spanische 200-Peseten-Münze zeigt auf beiden Seiten ein Siebeneck, ebenso haben die britischen 20-Pence- und 50-Pence-Stücke eine siebeneckige Form.
In der Architektur findet das Siebeneck sehr selten Verwendung. Der Konzertsaal „Hegelsaal“ im „Kultur- & Kongresszentrum Liederhalle“ in Stuttgart hat ebenso wie seine Glaskuppel einen Grundriss in Form eines regelmäßigen Siebenecks.
Die Diagonalen des regelmäßigen Siebenecks bilden das Heptagramm (siebenzackiger Stern), das als Symbol in der Esoterik populär ist.
Sternmotore wurden meistens als 5-, 7- oder 9-Zylinder gebaut.
Es gibt Fullerene (Kohlenstoffmoleküle), die siebeneckige Unterstrukturen aufweisen.[3]
Quellen
- ↑ Emil Artin: Galoissche Theorie. Verlag Harri Deutsch, Zürich 1973, ISBN 3-87144-167-8, S 85.
- ↑ C.J. Scriba, P. Schreiber 5000 Jahre Geometrie, Verlag Springer Berlin Heidelberg New York, 2. Auflage (2000?) ISBN 3-540-22471-8
- ↑ E. Albertazzi, C. Domene, P. W. Fowler, T. Heine, G. Seifert, C. Van Alsenoy and F. Zerbetto: Pentagon adjacency as a determinant of fullerene stability, Phys. Chem. Chem. Phys., 1999, 1, 2913-2918.
Weblinks
Wikimedia Foundation.