Hilbertkurve

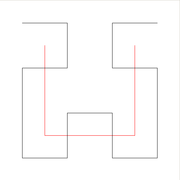
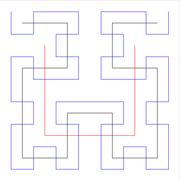
In der Mathematik ist die Hilbert-Kurve eine stetige Kurve, die – durch Wiederholung ihres Konstruktionsverfahrens – jedem beliebigen Punkt einer quadratischen Fläche beliebig nahe kommt und die Fläche vollständig ausfüllt. Die Hilbert-Kurve ist eine sogenannte raumfüllende oder FASS-Kurve. Sie wurde 1891 von dem deutschen Mathematiker David Hilbert entdeckt. Die Möglichkeit, mit einer stetigen eindimensionalen Kurve ein zweidimensionales Gebiet komplett abdecken zu können, war den Mathematikern des neunzehnten Jahrhunderts neu (siehe auch Monsterkurve).

Die euklidische Länge der Kurve H_n ist 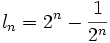$l_n = 2^n - {1 \over 2^n}$, d.h. wächst exponentiell mit n.

Mit der Entwicklung von Parallelrechnern haben raumfüllende Kurven wie die Hilbert-Kurve eine Anwendungsmöglichkeit erhalten, indem man sie zur Bestimmung der Lastverteilung der einzelnen Prozessoren nutzt.

Hilbert-Kurve 1. Ordnung

Hilbert-Kurven
1. und 2. Ordnung

Hilbert-Kurven 1. bis 3. Ordnung

• Siehe auch: Sierpiński-Kurve, Peano-Kurve, Z-Kurve

Weblinks

• Java-Applet zur Konstruktion von Hilbert-Kurven
• David Hilbert
• Hilbert- und Peano-Kurve
• Raumfüllende Kurven - TUM Informatik

Programmcode

Das folgende Java-Applet zeichnet eine Hilbert-Kurve mit vier rekursiven Methoden:

 import java.awt.*;
 import java.applet.*;
 
 public class HilbertKurve extends Applet {
     private SimpleGraphics sg=null;
     private int dist0=512, dist=dist0;
 
     public void init() {
         sg = new SimpleGraphics(getGraphics());
         dist0 = 512;
         resize ( dist0, dist0 );
     }
 
     public void paint(Graphics g) {
         int level=4;
         dist=dist0;
         for (int i=level;i>0;i--) dist /= 2;
         sg.goToXY ( dist/2, dist/2 );
         hilbertA(level);        //    Rekursion starten
     }
 
     private void hilbertA (int level) {
         if (level > 0) {
             hilbertB(level-1);    sg.lineRel(0,dist);
             hilbertA(level-1);    sg.lineRel(dist,0);
             hilbertA(level-1);    sg.lineRel(0,-dist);
             hilbertC(level-1);
         }
     }
 
     private void hilbertB (int level) {
         if (level > 0) {
             hilbertA(level-1);    sg.lineRel(dist,0);
             hilbertB(level-1);    sg.lineRel(0,dist);
             hilbertB(level-1);    sg.lineRel(-dist,0);
             hilbertD(level-1);
         }
     }
 
     private void hilbertC (int level) {
         if (level > 0) {
             hilbertD(level-1);    sg.lineRel(-dist,0);
             hilbertC(level-1);    sg.lineRel(0,-dist);
             hilbertC(level-1);    sg.lineRel(dist,0);
             hilbertA(level-1);
         }
     }
 
     private void hilbertD (int level) {
         if (level > 0) {
             hilbertC(level-1);    sg.lineRel(0,-dist);
             hilbertD(level-1);    sg.lineRel(-dist,0);
             hilbertD(level-1);    sg.lineRel(0,dist);
             hilbertB(level-1);
         }
     }
 }
 
 class SimpleGraphics {
     private Graphics g = null;
     private int x = 0, y = 0;    
 
     public SimpleGraphics(Graphics g) { this.g = g; }
     public void goToXY(int x, int y) { this.x = x;   this.y = y; }
 
     public void lineRel(int deltaX, int deltaY) {
         g.drawLine ( x, y, x+deltaX, y+deltaY );
         x += deltaX;    y += deltaY;
     }
 }

Das folgende Python-Programm zeichnet eine Hilbert-Kurve mit Hilfe von rekursiven Methoden:

from Tkinter import *
def hilbert(canvas,xa,ya,xe,ye,drehung,anz):
    global xalt,yalt
    if anz!=0:
        anz-=1
        xm=xa+(xe-xa)/2.0
        ym=ya+(ye-ya)/2.0
        if drehung==0:
            hilbert(canvas,xa,ym,xm,ye,1,anz)
            hilbert(canvas,xa,ya,xm,ym,0,anz)
            hilbert(canvas,xm,ya,xe,ym,0,anz)
            hilbert(canvas,xm,ym,xe,ye,2,anz)
        elif drehung==1:
            hilbert(canvas,xa,ym,xm,ye,0,anz)
            hilbert(canvas,xm,ym,xe,ye,1,anz)
            hilbert(canvas,xm,ya,xe,ym,1,anz)
            hilbert(canvas,xa,ya,xm,ym,3,anz)
        elif drehung==2:
            hilbert(canvas,xm,ya,xe,ym,3,anz)
            hilbert(canvas,xa,ya,xm,ym,2,anz)
            hilbert(canvas,xa,ym,xm,ye,2,anz)
            hilbert(canvas,xm,ym,xe,ye,0,anz)
        elif drehung==3:
            hilbert(canvas,xm,ya,xe,ym,2,anz)
            hilbert(canvas,xm,ym,xe,ye,3,anz)
            hilbert(canvas,xa,ym,xm,ye,3,anz)
            hilbert(canvas,xa,ya,xm,ym,1,anz)      
 
    else:
        xm=xa+(xe-xa)/2.0
        ym=ya+(ye-ya)/2.0
        if xalt!=0:
            canvas.create_line(xm,ym,xalt,yalt)
        xalt=xm
        yalt=ym
xalt=0
yalt=0
breite=512
hoehe=512
root=Tk()
canvas=Canvas(root,width=breite,height=hoehe,bg="white")
canvas.pack()
anzahl=8
hilbert(canvas,0,0,breite,hoehe,0,anzahl)
mainloop()