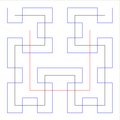
- Hilbert-Kurve
-

In der Mathematik ist die Hilbert-Kurve eine stetige Kurve, die – durch Wiederholung ihres Konstruktionsverfahrens – jedem beliebigen Punkt einer quadratischen Fläche beliebig nahe kommt und die Fläche vollständig ausfüllt. Die Hilbert-Kurve ist eine sogenannte raumfüllende oder FASS-Kurve. Sie wurde 1891 von dem deutschen Mathematiker David Hilbert entdeckt. Die Möglichkeit, mit einer stetigen eindimensionalen Kurve ein zweidimensionales Gebiet komplett abdecken zu können, war den Mathematikern des neunzehnten Jahrhunderts neu (siehe auch Monsterkurve).
Die euklidische Länge der Kurve Hn ist
 , d.h. wächst exponentiell mit n. Ihre Hausdorff-Dimension ist aufgrund der Eigenschaft, eine raumfüllende Kurve zu sein, exakt 2.
, d.h. wächst exponentiell mit n. Ihre Hausdorff-Dimension ist aufgrund der Eigenschaft, eine raumfüllende Kurve zu sein, exakt 2.Mit der Entwicklung von Parallelrechnern haben raumfüllende Kurven wie die Hilbert-Kurve eine Anwendungsmöglichkeit erhalten, indem man sie zur Bestimmung der Lastverteilung der einzelnen Prozessoren nutzt.
Siehe auch
Weblinks
Wikimedia Foundation.