Imaginäre Zahlen

Imaginäre Zahlen
Darstellung einer komplexen Zahl in der Gaußebene

In der Mathematik ist eine imaginäre Zahl eine Zahl, deren Quadrat eine negative reelle Zahl ist. Diese Bezeichnung wurde vermutlich von Cardano geprägt. In seinen Augen konnten solche Zahlen nicht existieren, sie konnten also nur imaginär (eingebildet) sein. Die imaginäre Zahl, die der 1 bei den reellen Zahlen entspricht, heißt auch imaginäre Einheit und wird mit i bezeichnet. In der Elektrotechnik wird gemäß DIN 1302 und DIN 5483-3 als Symbol statt i ein j benutzt, um eine Verwechslung mit der Stromstärke zu vermeiden.

Mit imaginären Zahlen lassen sich Gleichungen lösen, deren Lösungen keine reellen Zahlen sein können. Die Gleichung

x2 − 1 = 0

hat zur Lösung zwei reelle Zahlen, -1 und +1.

Die Gleichung

x2 + 1 = 0

hingegen kann keine reelle Lösung haben, da dazu die Wurzel aus einer negativen reellen Zahl gezogen werden müsste, denn die Wurzel ist die Umkehrfunktion des Quadrierens – und Quadrate sind immer positiv. Ihre Lösungen sind 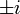\pm i, zwei imaginäre Zahlen.

Eine Beschäftigung mit Quadratwurzeln aus negativen Zahlen wurde bei der Lösung von kubischen Gleichungen im Fall des Casus irreducibilis nötig.

Heute versteht man imaginäre Zahlen als spezielle komplexe Zahlen. Jede komplexe Zahl kann dargestellt werden als Summe einer reellen Zahl und eines reellen Vielfachen der imaginären Einheit i, einer Zahl mit der Eigenschaft:

i2 = − 1

Die imaginäre Einheit wird oft auch als diejenige Zahl, die mit sich selbst multipliziert -1 ergibt, verstanden. Entgegen der allgemeinen Meinung ist i nicht die Quadratwurzel (Wurzel) von -1, da die Wurzel von a als „diejenige positive Zahl, die mit sich selbst multipliziert a ergibt“, definiert ist – allerdings führen sowohl i > 0 als auch i < 0 zu Widersprüchen. i kann daher weder positiv noch negativ sein.

Algebraisch wird i definiert als eine Nullstelle des Polynoms x2 + 1, und die Komplexen Zahlen als die dadurch erzeugte Körpererweiterung. Die zweite Nullstelle ist dann automatisch − i. Man kann sie aber erst unterscheiden, wenn man eine der beiden mit i bezeichnet hat. Da man sie aber ohnehin nicht unterscheiden kann, spielt es keine Rolle „welche“ Nullstelle man nun mit i bezeichnet.

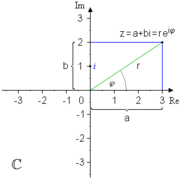
Alle komplexen Zahlen lassen sich in der Gaußebene darstellen, einer Erweiterung der reellen Zahlengeraden (siehe Abbildung rechts). Die komplexe Zahl a + i \cdot b hat den Realteil a und den Imaginärteil b. Aufgrund der Rechenregeln komplexer Zahlen ist das Quadrat einer Zahl, deren Realteil gleich 0 ist, eine nicht positive reelle Zahl:

(bi)2 = − b2.

Die imaginären Zahlen bilden also eine Gerade, die durch die Zahl 0 geht und senkrecht auf der reellen Zahlengeraden steht.

Eine weitergehende Beschreibung findet sich im Artikel über komplexe Zahlen.

Quaternionen

Die Quaternionen kennen drei imaginäre Einheiten: i,j und k.


Wikimedia Foundation.

Игры ⚽ Нужна курсовая?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • imaginäre Zahlen — imaginäre Zahlen,   diejenigen komplexen Zahlen, deren Realteil null ist und die sich in der Form b · i (mit b als reelle Zahl) schreiben lassen; insbesondere nennt man die imaginären Zahlen i2 = 1 die imaginäre Einheit. Ist z eine …   Universal-Lexikon

  • Imaginäre Zahl — Eine imaginäre Zahl ist eine Zahl, deren Quadrat eine nicht positive reelle Zahl ist. Diese Bezeichnung wurde vermutlich von Cardano geprägt. Nach seiner Ansicht konnten solche Zahlen nicht existieren, sie konnten also nur imaginär (eingebildet)… …   Deutsch Wikipedia

  • Imaginäre Einheit — Darstellung einer komplexen Zahl in der Gaußebene In der Mathematik ist eine imaginäre Zahl eine Zahl, deren Quadrat eine negative reelle Zahl ist. Diese Bezeichnung wurde vermutlich von Cardano geprägt. In seinen Augen konnten solche Zahlen… …   Deutsch Wikipedia

  • Imaginäre Zeit — Die Wick Rotation ist eine Methode für die Herleitung einer Lösung eines Problems im Minkowski Raum aus der Lösung eines verwandten Problems im Euklidschen Raum durch analytische Fortsetzung. Benannt wurde sie nach Gian Carlo Wick. Die Wick… …   Deutsch Wikipedia

  • Imaginäre Größen — Imaginäre Größen, Größen, die nicht reell sind, die man also weder durch positive noch durch negative Zahlen darstellen kann. Von imaginären Punkten, Geraden etc. spricht man in der analytischen Geometrie, um auch solchen Gleichungen, die nicht… …   Meyers Großes Konversations-Lexikon

  • imaginäre Zahl — imaginäre Zahl,   komplexe Zahlen …   Universal-Lexikon

  • Besondere Zahlen — sind zum einen Zahlen, die im Sinne der Zahlentheorie eine oder mehrere auffällige Eigenschaften besitzen. Außerdem haben viele Zahlen eine besondere Bedeutung in der Mathematik und/oder in Bezug auf die reale Welt. Diese letzteren Zahlen werden… …   Deutsch Wikipedia

  • Liste besonderer Zahlen — Besondere Zahlen sind zum einen Zahlen, die im Sinne der Zahlentheorie eine oder mehrere auffällige Eigenschaften besitzen. Außerdem haben viele Zahlen eine besondere Bedeutung in der Mathematik oder in Bezug auf die reale Welt. Diese letzteren… …   Deutsch Wikipedia

  • Irreelle Zahlen — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… …   Deutsch Wikipedia

  • Komplexe Zahlen — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”