- Intervallsuche
-
Die Interpolationssuche, auch Intervallsuche genannt, ist ein von der binären Suche abgeleitetes Suchverfahren, das auf Listen und Feldern zum Einsatz kommt.
Während der Algorithmus der binären Suche stets das mittlere Element des Suchraums überprüft, versucht der Algorithmus der Interpolationssuche im Suchraum einen günstigeren Teilungspunkt als die Mitte zu erraten. Die Arbeitsweise ist mit der eines Menschen vergleichbar, der ein Wort in einem Wörterbuch sucht: Die Suche nach einem mit Z beginnenden Wort wird üblicherweise am Ende des Wörterbuches begonnen, während die Suche nach Aal im vorderen Bereich begonnen werden dürfte.
Inhaltsverzeichnis
Der Algorithmus
Die Interpolationssuche geht von sortierten und gleichverteilten Daten aus. Des Weiteren wird ein wahlfreier Zugriff auf die Elemente vorausgesetzt. Die Daten werden bei der Interpolationssuche in Abhängigkeit vom Schlüssel geteilt. Hat dieser einen großen Wert, befindet sich das gesuchte Element aufgrund der Vorsortierung im hinteren Teil der Daten. Dementsprechend wird auch im hinteren Teil der Daten die Teilung vorgenommen. Bei einem kleinen Schlüssel wird das Feld entsprechend im vorderen Teil gespalten.
Für alle Daten lässt sich die Teilungsposition berechnen, indem zunächst die Anzahl aller Elemente durch die Anzahl verschiedener Elemente dividiert wird, und anschließend mit dem gesuchten Schlüssel multipliziert wird:

Die Position des gesuchten Elementes wird somit interpoliert, indem die Gleichverteilung der Daten für eine Abbildung des Schlüssels auf die Liste bzw. das Feld genutzt wird.
Nun kann überprüft werden, ob der Schlüssel des teilenden Elementes einen größeren oder kleineren Wert als der Schlüssel des gesuchten Elementes hat. Bei identischen Schlüsseln ist die Suche bereits beendet. Wenn das teilende Element einen kleineren Wert hat, wird der rechte Teilbereich weiteruntersucht, andernfalls der linke Teilbereich. Die Zahl der Elemente sowie die Zahl der verschiedenen Schlüssel wird für den neuen Bereich ermittelt, und anschließend eine neue Teilungsposition interpoliert.
Beispiel
Ein kurzes praktisches Beispiel soll die Arbeitsweise der Interpolationssuche veranschaulichen.
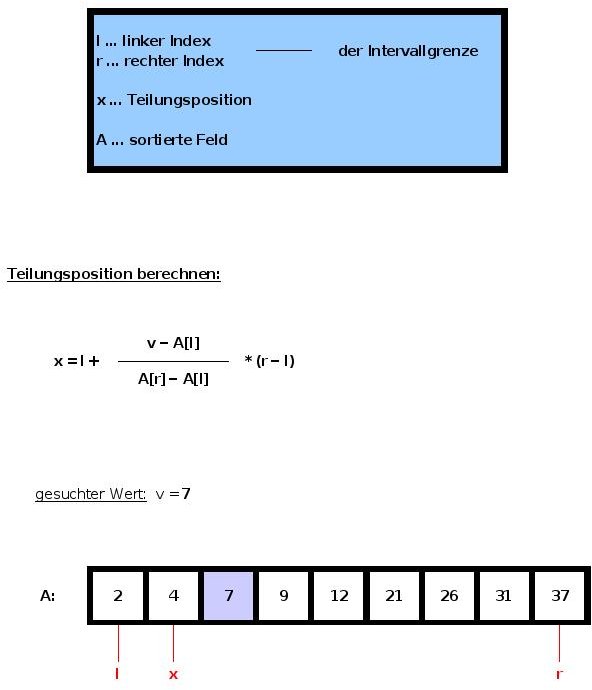
Ausgehend von der sortierten Folge A mit der linken (l) und rechten (r) Intervallsgrenze berechnet sich die erste Teilungsposition im folgenden Beispiel wie folgt:
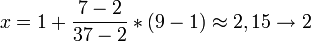
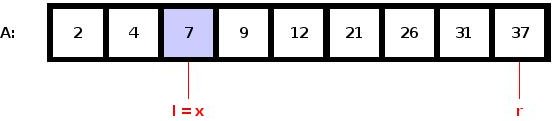
Der Teilungspunkt ist also A[x=2] = 4 wie oben im Bild gekennzeichnet. Da v > A[x] ist wird die rechte Hälfte gewählt und der Teilungspunkt neu berechnet.
Neuer Teilungspunkt: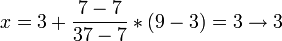
A[x] = v die Suche nach dem Element 7 ist beendet.
die Suche nach dem Element 7 ist beendet.Komplexität
Eine Untersuchung der Interpolationssuche erweist sich als sehr komplex, als Laufzeit kann jedoch
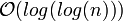 (n ist die Anzahl der Elemente) im durchschnittlichen Fall angenommen werden. Im ungünstigsten (die interpolierte erwartete Position ist immer am Rand) Fall beträgt die Laufzeit allerdings
(n ist die Anzahl der Elemente) im durchschnittlichen Fall angenommen werden. Im ungünstigsten (die interpolierte erwartete Position ist immer am Rand) Fall beträgt die Laufzeit allerdings 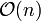 . Diese Beeinträchtigung löst die Quadratische Binärsuche.
. Diese Beeinträchtigung löst die Quadratische Binärsuche.Beispielimplementierungen
VB.NET 2008
'Statt einer List(Of Integer) könnte auch IEnumerable(Of Integer), etc. verwendet werden. IEnumerable ermöglicht die Übergabe 'sowohl von generischen Listen, als auch Arrays Public Function InterpolatedSearch(ByVal key As Integer, ByVal array As List(Of Integer)) As Integer Dim left As Integer = 0 Dim right As Integer = array.Count - 1 Dim diffElem, position As Integer Do While (key >= array(left)) AndAlso (key <= array(right)) diffElem = array(right) - array(left) position = left + Math.Floor((right - left) * (key - array(left) / diffElem) If key > array(pos) Then left = pos + 1 ElseIf key < array(pos) right = pos - 1 Else Return pos End If Loop Return -1 End FunctionJava
public int interpolierteSuche(int schluessel, int daten[]) { int links = 0; // linke Teilfeldbegrenzung int rechts = daten.length - 1; // rechte Teilfeldbegrenzung int versch; // Anzahl verschiedener Elemente int pos; // aktuelle Teilungsposition // solange der Schlüssel im Bereich liegt (andernfalls ist das gesuchte // Element nicht vorhanden) while( schluessel >= daten[links] && schluessel <= daten[rechts] ){ // Aktualisierung der Anzahl der verschiedenen Elemente versch = daten[rechts] - daten[links]; // Berechnung der neuen interpolierten Teilungsposition pos = links + (int)(((double)rechts - links) * (schluessel - daten[links]) / versch); if( schluessel > daten[pos] ) // rechtes Teilintervall links = pos + 1; // daten[pos] bereits überprüft else if( schluessel < daten[pos] ) // linkes Teilintervall rechts = pos - 1; // daten[pos] bereits überprüft else // Element gefunden return pos; // Position zurückgeben } return -1; // Element nicht gefunden }
Delphi
type TIntArray = array of integer; function interpolierteSuche(schluessel: integer; var daten: TIntArray): integer; var links, rechts, versch, aPos: integer; begin links := 0; rechts := high(daten); versch := 0; aPos := 0; while (schluessel >= daten[links]) and (schluessel <= daten[rechts]) do begin versch := daten[rechts] - daten[links]; aPos := links + round((rechts - links) * (schluessel - daten[links]) / versch); if (schluessel > daten[aPos]) then links := aPos + 1 else if (schluessel < daten[aPos]) then rechts := aPos - 1 else begin result := aPos; exit; end; end; result := - 1; end;
C
/** * Liefert 1 zurück, wenn X in M gefunden wurde, ansonsten 0. * Beim Aufruf wird als 4. Argument eine Variable per Adresse * übergeben, in die bei Erfolg die Position von X in M geschrieben wird. * @param const int[] M Feld, in dem gesucht werden soll * @param int n Groesse des Feldes * @param int X der gesuchte Eintrag * @param int * index Position des gesuchten Eintrags X in M * @return int 1=gefunden, 0=nicht gefunden */ int interpolation_search( const int M[], int n, int X, int *index ) { double dx, dy; double m; // Steigung double b; // Y-Achsenabschnitt int links = 0; // x1 int rechts = n-1; // x2 int pos; // vermutete Position if ( M==NULL || X < M[0] || X > M[n-1] ) { return 0; } while ( links <= rechts ) { dx = rechts - links; if ( dx == 1 ) { if ( M[rechts] == X ) { *index = rechts; return 1; } else if ( M[links] == X ) { *index = links; return 1; } return 0; } if ( dx == 0 ) // 0 Division vorbeugen { return 0; } dy = M[rechts] - M[links]; if ( dy == 0 ) // keine Steigung { if ( M[links] == X ) { *index = links; return 1; } else { return 0; } } m = dy / dx; // Steigung b = (X - M[links]) / m; pos = links + b; // Vermutete Position berechnen if ( M[pos] == X ) { *index = pos; return 1; } else if ( M[pos] > X ) { rechts = pos - 1; } else { links = pos + 1; } } return 0; }
Literatur
Robert Sedgewick: Algorithmen in C. Addison-Wesley, 1992, S. 239-241
Siehe auch
Weblinks
Wikimedia Foundation.