Intervallskalenniveau

Die Intervallskala (z. T. auch Kardinalskala) ist eine der fünf wichtigsten Skalenniveaus in der Statistik. Sie zählt zum metrischen Messniveau, da sich die Ausprägungen dieses Skalenniveaus quantitativ mittels Zahlen darstellen lässt. Das heißt insbesondere auch, dass Rangunterschiede und Abstand zwischen Werten gemessen werden können, d. h. quantitative Merkmale gehen in ihren Anforderungen über ordinale oder gar nominale Eigenschaften hinaus.

Beschreibung

Bei intervallskalierten Merkmalen lassen sich zusätzlich zu den Eigenschaften der Ordinalskala die Abstände zwischen den verschiedenen Merkmalsausprägungen exakt bestimmen. Allerdings existiert kein natürlicher Nullpunkt für die Skala. Willkürlich definierte Nullpunkte, wie z. B. bei der Celsius-Temperaturskala zählen hier nicht als natürlicher Nullpunkt, während der Nullpunkt der Kelvin-Temperaturskala, der dem absoluten Nullpunkt entspricht, ein natürlicher Nullpunkt ist.

Sind zwei Datenpaare (a,b) und (c,d) äquivalent (siehe unten) dann ist bei Intervallskalen der Quotienten aus Differenzen (a-b)/(c-d) immer gleich.

Zulässige Aussagen bei Intervallskalen lassen sich an folgendem Beispiel illustrieren, Dabei werden zwei Intervallskalen in einem zweiten Schritt in ein Verhältnis gesetzt (Verhältnisskala). Dies entspricht einer weiteren Datenverarbeitung der Intervallskala: Wir kennen die Temperaturen von Tag A, Tag B und Tag C. Jetzt bilden wir das Verhältnis der Differenzen: (A-B) / (A-C). Angenommen, das Verhältnis ist 2. Dann wäre eine zulässige Aussage: „Der Temperaturunterschied zwischen Tag A und B ist doppelt so groß wie der Temperaturunterschied zwischen Tag A und C.“

Jede Intervallskala ist so geartet, dass die Rangfolge der Differenz zwischen Zahlen gleich der Rangfolge der Merkmalsunterschiede zwischen den entsprechenden Objekten ist. Damit wird eine Ordnung auf den Paaren (a,b) aus der Skala definiert (siehe auch Ordnungsrelation.

Beispiele

Beispiele für intervallskalierte Merkmale mit einer mathematischen Paarbildung 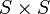$S \times S$ aus der Skala S sind:

• Temperatur auf der Celsius-Skala mit $(Temperatur_{12:00 Uhr}, Temperatur_{6:00 Uhr})\in S \times S$,
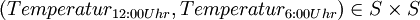• Jahreszahlen mit $(Sterbejahr,Geburtsjahr)\in S \times S$
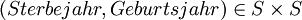
• Zeitpunkte $(Zielzeit,Startzeit)\in S \times S$
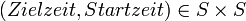
• IQ-Skala

Mögliche Operationen

Zusätzlich zu Größenvergleichen sind Differenzen und Summen aus intervallskalierten Merkmalen sinnvoll, da hier die Abstände zwischen den einzelnen Merkmalsausprägungen exakt definiert sind. Damit lassen sich hier auch Durchschnittswerte berechnen. Aufgrund des fehlenden Nullpunkts stellt die Multiplikation keine sinnvolle Operation für intervallskalierte Merkmale dar.

Ein kleines Beispiel möge das verdeutlichen: War es z. B. gestern 10 Grad Celsius und Heute ist es zwanzig Grad, dann kann man zwar behaupten: „Es ist zehn Grad Celsius wärmer“, aber nicht: „Es ist doppelt so warm wie gestern“. Dies wird besonders deutlich wenn man Celsius in Kelvin oder Fahrenheit transformiert.

Erlaubte Transformationen

Zulässig sind positiv-lineare Transformationen der Art y = αx + β

Mathematische Deutung

Aus mathematischer Sicht ist eine Intervallskala S eine Menge, für die folgendes gilt:

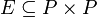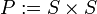1. Es existiert eine Äquivalenzrelation $E \subseteq P \times P$ mit $P:=S \times S$ (Menge der Paare aus S). 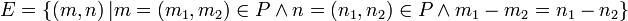$E = \left\{ \left(m,n\right) \vert m=(m_1,m_2) \in P \wedge n=(n_1,n_2) \in P \wedge m_1-m_2=n_1-n_2\right\}$ (Nominalskalen-Eigenschaft). Bezogen auf das Beispiel 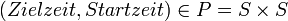$(Zielzeit,Startzeit)\in P=S \times S$ werden alle Paare (Zielzeit,Startzeit) zu einer Äquivalenzklasse zusammengefasst, die die gleiche Zeitdauer benötigt haben, also z. B. m = (m₁,m₂) = (20,7) und n = (n₁,n₂) = (30,17) sind in einer Äquivalenzklasse (formal: 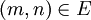$(m,n)\in E$), weil beide Datenpaare m und n die gleiche Zeitdauer zwischen Start und Ziel benötigt haben. Siehe auch Differenzfunktion.
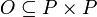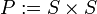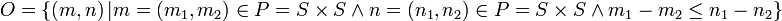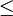2. Es existiert eine lineare Ordnungsrelation $O \subseteq P \times P$ mit $P:=S \times S$ (Ordinalskalen-Eigenschaft). $O = \left\{ \left(m,n\right) \vert m=(m_1,m_2) \in P = S\times S \wedge n=(n_1,n_2) \in P = S\times S \wedge m_1-m_2 \leq n_1-n_2\right\}$. Die $\leq$-Beziehung kann z. B. auch durch eine andere Ordnungsrelation auf der Differenz in D ersetzt werden (z. B. 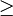$\geq$), wenn die mathematischen Eigenschaften der Ordnungsrelation erhalten bleiben. Bezogen auf das Beispiel 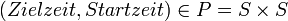$(Zielzeit,Startzeit)\in P=S \times S$ werden alle Paare (Zielzeit,Startzeit) bezogen auf die Zeitdifferenz geordnet, also z. B..mit m = (m₁,m₂) = (40,37) und n = (n₁,n₂) = (30,7) wäre 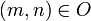$(m,n)\in O$ (m ist kleiner als n), weil m weniger Zeit zwischen Start und Ziel benötigt hat als n. Es wird eine Ordnungsrelation auf der Menge der Zahlenpaare in P über die Differenz der Komponenten von m bzw. n definiert (siehe nachfolgende Definition der Differenzfunktion auf $S\times S$).

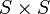1. Intervallskalen-Eigenschaft:
   1. Es existiert eine Funktion (Differenzfunktion) 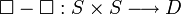$\Box -\Box :S \times S \longrightarrow D$ (Man kann Differenzen bilden, z. B. 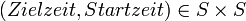$(Zielzeit,Startzeit)\in S \times S$ wird der Zeitdauer 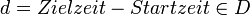$d=Zielzeit-Startzeit\in D$ zugeordnet).
   2. Es existiert eine Funktion (Mengentheorie)|Funktion 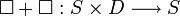$\Box +\Box :S \times D \longrightarrow S$ (Man kann die Differenzen wieder auf Ausprägungen von S addieren), für die außerdem gilt:
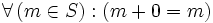      1. $\forall\left(m \in S\right):\left( m+0 = m \right)$ (Das Addieren von Null bringt keine Änderung)
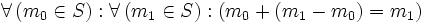      2. $\forall\left(m_0 \in S\right):\forall\left(m_1 \in S\right):\left( m_0+\left(m_1-m_0\right) = m_1 \right)$ (Differenzbildung ist konsistent mit Aufaddierung).
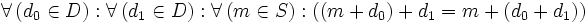      3. $\forall\left(d_0 \in D\right):\forall\left(d_1 \in D\right):\forall\left(m \in S\right):\left( \left(m+d_0\right)+d_1 = m+\left(d_0+d_1\right) \right)$ (eine Art einseitiges Assoziativgesetz)
   3. Die Menge der Differenzen D ist den reellen Zahlen in folgender Hinsicht ähnlich:
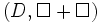      1. $\left( D, \Box + \Box \right)$ ist ein Untermonoid von 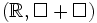$\left(\mathbb{R},\Box + \Box\right)$ (reelle Zahlen mit der Addition).

Jedes Element 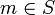$m \in S$ heißt Ausprägung von S.

Jede Intervallskala (S, − ) ist eine Ordinalskala S mit einer Differenzfunktion − auf $S \times S$.

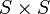Siehe auch

• ordinales Merkmal
• nominales Merkmal

Skalenniveaus

Nominalskala | Ordinalskala | Intervallskala | Verhältnisskala | Absolutskala