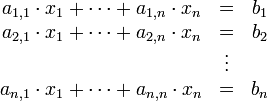Jacobiverfahren

In der numerischen Mathematik ist das Jacobi-Verfahren, auch Gesamtschrittverfahren genannt, (benannt nach Carl Gustav Jakob Jacobi) ein Algorithmus zur näherungsweisen Lösung von linearen Gleichungssystemen Ax = b. Es ist, wie das Gauß-Seidel-Verfahren und das SOR-Verfahren, ein spezielles Splitting-Verfahren.

Entwickelt wurde das Verfahren, da das Gaußsche Eliminationsverfahren zwar eine exakte Lösungsvorschrift ist, sich für Rechenfehler jedoch sehr anfällig zeigt. Eine iterative Vorgehensweise hat diesen Nachteil typischerweise nicht.

Beschreibung des Verfahrens

Gegeben ist ein lineares Gleichungssystem mit n Variablen mit n Gleichungen.

$\begin{matrix} a_{1,1}\cdot x_1+\dots+a_{1,n}\cdot x_n&=&b_1\\ a_{2,1}\cdot x_1+\dots+a_{2,n}\cdot x_n&=&b_2\\ &\vdots&\\ a_{n,1}\cdot x_1+\dots+a_{n,n}\cdot x_n&=&b_n\\ \end{matrix}$

Um dieses zu lösen, wird die i-te Gleichung nach der i-ten Variablen x_i aufgelöst,

$x_i^{(m+1)}:=\frac1{a_{i,i}}\left(b_i-\sum_{j\not=i} a_{i,j}\cdot x_j^{(m)}\right)$,

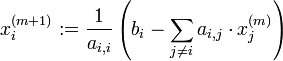und diese Ersetzung, ausgehend von einer willkürlichen Startbelegung x⁽⁰⁾ der Variablen, periodisch wiederholt. Als minimale Bedingung lässt sich hier festhalten, dass die Diagonalelemente a_i,i von Null verschieden sein müssen. Für die Konvergenz des Verfahrens ist die strikte Diagonaldominanz der Systemmatrix hinreichend.

Als Algorithmusskizze mit c Iterationen und n Zeilen bzw. Spalten ergibt sich:

für m=1 bis c 
  für i=1 bis n
    xi = 0
       für j=1 bis n
         falls j != i
            $x_i=x_i+a_{i,j}x_j^{(m-1)}$;
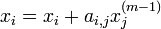       end
       xi = (bi − xi) / ai,i;
  end
  x(m) = x;
end

Dabei wurde die willkürliche Erstbelegung des Variablenvektors als Eingangsgrößen des Algorithmus angenommen, die Näherungslösung ist die vektorielle Rückgabegröße.

Beschreibung in Matrixschreibweise

Die Matrix 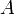$A\,$ des linearen Gleichungssystems 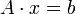$A \cdot x = b$ wird zur Vorbereitung in eine Diagonalmatrix D, eine strikte untere Dreiecksmatrix L und eine strikte obere Dreiecksmatrix U zerlegt, so dass gilt:

$A\,=\, L+D+U$.

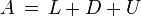Die obige komponentenweise Iterationsvorschrift lässt sich dann folgendermaßen für den kompletten Vektor darstellen:

$x^{(m+1)} = D^{-1} \left( b - \left(L + U\right) x^{(m)} \right)$.

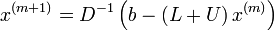Konvergenzuntersuchung

Die Konvergenz wird wie bei allen Splitting-Verfahren mittels des banachschen Fixpunktsatzes untersucht. Das Verfahren konvergiert also, wenn der Spektralradius der Iterationsmatrix D ^{− 1}(D − A) kleiner als eins ist. Insbesondere ergibt sich dies, wenn die Systemmatrix A strikt diagonaldominant ist.

Literatur

• A. Meister: Numerik linearer Gleichungssysteme, 2. Auflage, Vieweg 2005, ISBN 3528131357
• R. Barrett et al.: Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd Edition, SIAM Philadelphia, 1994

Weblinks

• Eric W. Weisstein et al. "Jacobi Method" MathWorld
• Gesamt- und Einzelschrittverfahren bzw. Jacobi- und Gauss-Seidel-Verfahren fuer N = 3 (pdf) Jacobi und Gauss-Seidel-Verfahren verstaendlich erklaert, inklusive Matlab Programme.