- Diagonaldominanz
-
Diagonaldominanz bezeichnet in der Mathematik eine Eigenschaft von quadratischen Matrizen, welche vor allem in der Numerik Einsatz findet. Der alleinstehende Begriff diagonaldominant wird in der Literatur uneinheitlich mal für strikt diagonaldominant und mal für schwach diagonaldominant verwendet. Im Folgenden werden beide Begriffe näher erläutert.
strikt diagonaldominant
Eine
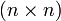 -Matrix A = (aij) heißt strikt (auch: streng oder stark) diagonaldominant, falls die Beträge ihrer Diagonalelemente aii jeweils größer sind als die Summe der Beträge der restlichen jeweiligen Zeileneinträge aij, d.h. wenn für alle
-Matrix A = (aij) heißt strikt (auch: streng oder stark) diagonaldominant, falls die Beträge ihrer Diagonalelemente aii jeweils größer sind als die Summe der Beträge der restlichen jeweiligen Zeileneinträge aij, d.h. wenn für alle 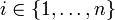 gilt
gilt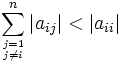 .
.
Dieses Kriterium wird auch als starkes Zeilensummenkriterium bezeichnet und ist nicht äquivalent zu dem entsprechenden Spaltensummenkriterium, jedoch nach Definition äquivalent zum Spaltensummenkriterium der transponierten Matrix.
Komplexe, strikt diagonaldominante Matrizen sind regulär, ebenso die aus ihnen durch Nullsetzen bestimmter Einträge gewonnenen oberen und unteren Dreiecksmatrizen. Bei einigen Verfahren zum Lösen von Gleichungssystemen (z. B. Gauß-Seidel-, Jacobi- oder SOR-Verfahren) bietet die Diagonaldominanz der Systemmatrix, insbesondere die letztgenannte Eigenschaft, ein hinreichendes Kriterium für die Konvergenz des Verfahrens.schwach diagonaldominant
Eine
 -Matrix A = (aij) heißt schwach diagonaldominant, falls die Beträge ihrer Diagonalelemente aii jeweils größer als die oder gleich der Summe der Beträge der restlichen jeweiligen Zeileneinträge aij sind, d.h. wenn für alle
-Matrix A = (aij) heißt schwach diagonaldominant, falls die Beträge ihrer Diagonalelemente aii jeweils größer als die oder gleich der Summe der Beträge der restlichen jeweiligen Zeileneinträge aij sind, d.h. wenn für alle 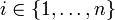 gilt
gilt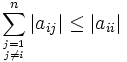 .
.
Die Menge der schwach diagonaldominanten Matrizen umfasst also die Menge der strikt diagonaldominanten Matrizen.
Reelle, symmetrische, schwach diagonaldominante Matrizen mit nichtnegativen Diagonaleinträgen sind positiv semidefinit.irreduzibel diagonaldominant
In der Numerik partieller Differenzialgleichungen wird zudem für Stabilitätsbetrachtungen ein weiterer Begriff verwendet: Eine
 -Matrix A = (aij) heißt irreduzibel diagonaldominant, wenn sie irreduzibel und schwach diagonaldominant ist und für ein
-Matrix A = (aij) heißt irreduzibel diagonaldominant, wenn sie irreduzibel und schwach diagonaldominant ist und für ein 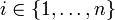 die Ungleichung
die Ungleichung 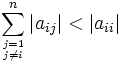 gilt.
gilt.
Wikimedia Foundation.
