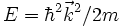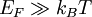Jellium-Modell

In der Festkörperphysik bezeichnet der Begriff Elektronengas eine Modellvorstellung für die frei beweglichen Elektronen im Leitungsband von Metallen oder Halbleitern. Im Rahmen dieses Modells werden die frei beweglichen Elektronen als Grund für die Leitfähigkeit von Metallen verstanden, und der elektrische Widerstand wird durch die Streuung von Elektronen an Phononen und Kristall-Fehlstellen beschrieben. Das Elektronengas ist kein Gas im chemischen Sinn.

Delokalisierte Elektronen

Elektronen im Leitungsband sind delokalisiert, d.h. sie sind nicht zu einem lokalisierten Gitteratom zuzuordnen. (Streng genommen sind aber im Festkörper alle Elektronen delokalisiert.) Ein freies, nicht wechselwirkendes Elektron besitzt eine (kinetische) Energie E und einen (quantenmechanischen) Wellenvektor 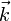$\vec k$. Sie hängen über die sog. Dispersionsrelation

$E=\hbar^2\vec k^2/2m$

zusammen. Relationen dieser Art bestimmen die Bandstruktur im Wellenvektorenraum. Das beschriebene freie Elektronengas (mit dem parabolischen Band) ist nur ein einfaches Modell für die Elektronen im Leitungsband. In komplizierteren Modellen (z.B. Näherung quasi-freier Elektronen oder Tight-Binding-Modell), die die Wirklichkeit besser beschreiben, wird das periodische Potenzial des Kristalls berücksichtigt, was zu komplexeren Bandstrukturen führt. Diese können jedoch in erster Näherung um 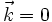$\vec k=0$ auch durch obige parabolische Dispersion beschrieben werden, wenn für m die effektive Masse des jeweiligen Bandes gesetzt wird.

Da Elektronen Fermionen sind, können keine zwei Elektronen in allen Quantenzahlen übereinstimmen. Dadurch sind die Energieniveaus bei Temperatur T = 0 K von 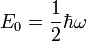$E_{0}=\frac{1}{2}\hbar\omega$ (Nullpunktsenergie) her aufgefüllt bis zur sogenannten Fermienergie. Die Verteilung der Energie wird durch die Fermi-Dirac-Statistik beschrieben, die bei T > 0 K an der „Fermikante“ in einem Bereich der Breite ~ 2kT, aufgeweicht ist.

Entartetes Elektronengas

Man bezeichnet ein Elektronengas als entartet, wenn die Fermienergie der Elektronen in einem Potentialkasten viel größer ist als die absolute Temperatur multipliziert mit dem Boltzmannfaktor.

$E_F \gg k_B T$

mit

E_F : Fermienergie

k_B : Boltzmannkonstante

T : absolute Temperatur

Insbesondere ist jedes Elektronengas bei T → 0 entartet.

Siehe auch

• Bänderdiagramm
• Leiter (Physik)
• reziproker Raum
• Brillouin-Zone
• Kronig-Penney-Modell
• Bosegas
• Quantenpunkt, Quantendraht, Zweidimensionales Elektronengas