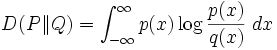KL-Divergenz

Die Begriffe Kullback-Leibler-Divergenz (kurz KL-Divergenz), Kullback-Leibler-Entropie, Kullback-Leibler-Information oder Kullback-Leibler-Abstand (nach Solomon Kullback und Richard Leibler) bezeichnen ein Maß für die Unterschiedlichkeit zweier Wahrscheinlichkeitsverteilungen desselben Ereignishorizonts. Typischerweise repräsentiert P Beobachtungen oder eine präzise Wahrscheinlichkeitsverteilung, während Q ein Modell oder eine Approximation darstellt.

Vorsicht: Die KL-Divergenz wird auch relative Entropie genannt, wobei der Begriff relative Entropie gelegentlich auch für die Transinformation verwendet wird.

Formal lässt sich die KL-Divergenz für die Wahrscheinlichkeitsfunktionen P und Q diskreter Werte folgendermaßen bestimmen:

$D(P\|Q) = KL(P, Q)= \sum_{x \in X} P(x) \log {P(x) \over Q(x)}$.

Werden die Verteilungen P und Q für kontinuierliche Werte durch die Wahrscheinlichkeitsdichtefunktionen p und q dargestellt, wird hingegen ein Integral berechnet:

$D(P\|Q) = \int_{-\infty}^{\infty} p(x) \log \frac{p(x)}{q(x)} \; dx \!$

Die Kullback-Leibler-Divergenz gibt aus informationstheoretischer Sicht an, wieviele Bits durchschnittlich verschwendet werden, wenn eine eigentlich auf q basierende Kodierung auf Ereignisse angewendet wird, die p folgen. Somit besteht ein Zusammenhang zur Kanalkapazität.

Anstatt der Kullback-Leibler-Divergenz wird auch oft die Kreuzentropie verwendet. Diese liefert qualitativ vergleichbare Werte, kann jedoch ohne die Kenntnis von p berechnet werden. In praktischen Anwendungen ist dies vorteilhaft, da dort p meist unbekannt ist.

Belege

• S. Kullback, R. A. Leibler: On information and sufficiency. In: Annals of Mathematical Statistics. 22, Nr. 1, März 1951, S. 79–86. 
• S. Kullback; John Wiley & Sons (Hrsg.): Information theory and statistics. 1959. 
• Springer Online Reference Works. eom.springer.de. Abgerufen am 31. März 2008. (englisch)