- Kleines Einmaleins
-
Das kleine Einmaleins ist ein Sammelbegriff für alle Produkte zweier Zahlen von 1 bis 10. Als großes Einmaleins gelten alle Multiplikationen von je zwei Zahlen zwischen 1 und 20. Das Kleine Einmaleins gehört zum arithmetischen Grundwissen der Mathematik und wird meist in der Grundschule auswendig gelernt. Als Einmaleins werden metaphorisch auch Grundkenntnisse eines Wissensgebiets oder einer Fertigkeit bezeichnet.
Inhaltsverzeichnis
Anwendung
Die meisten praktisch-arithmetischen Berechnungen sind ohne Kenntnis des kleinen Einmaleins nur umständlich durchführbar. Beim schriftlichen Multiplizieren wird die Hauptaufgabe in Produkte einstelliger Zahlen und in Summen zerlegt. Anstatt die Produkte nun in jedem Schritt zu berechnen, ist es effektiver, die Ergebnisse auswendig zu lernen, da das Erinnern ein viel schnellerer Vorgang ist als das Berechnen. Ähnlich verfährt man bei der schriftlichen Division.
Dieser Kniff wird auch in der Computertechnik angewendet. Dort speichert man häufig benötigte Ergebnisse von Zwischenschritten in einem sogenannten Cache, aus dem dann schneller gelesen werden kann als das Ergebnis neu zu berechnen.
Um das kleine Einmaleins in der Bruchrechnung effektiv einzusetzen, müssen die Beziehungen auch rückwärts gelernt werden, also beispielsweise 54 = 6 · 9, da man hier vom schnellen Faktorisieren profitiert.
Beim Überschlagen wendet man dieselben Techniken wie bei der Multiplikation und Division an, jedoch beschränkt man sich auf diejenigen Teilschritte, welche für eine auf die Schnelle benötigte Genauigkeit ausreichen. Beispiel: Gesucht ist das Ergebnis von 549839 : 7. Die Zahl 549839 liegt nahe bei 560000. Man weiß aus dem Einmaleins: 7 · 8 = 56. Das Ergebnis liegt also etwas unterhalb von 80000.
Tabellarische Darstellung
Als Tabelle wird das Einmaleins unterteilt in die 2er-Reihe, 3er-Reihe, 4er-Reihe usw. bis zur 10er-Reihe. Die 2er-Reihe besteht dabei aus 1 · 2 = 2, 2 · 2 = 4, 3 · 2 = 6 usw. bis 10 · 2 = 20, die 3er-Reihe entsprechend aus 1 · 3 = 3, 2 · 3 = 6, 3 · 3 = 9 usw.
Die folgende Multiplikationstabelle dient dem raschen Ermitteln von Produkten mit Faktoren bis 12.
· 1 2 3 4 5 6 7 8 9 10 11 12 1 1 2 3 4 5 6 7 8 9 10 11 12 2 2 4 6 8 10 12 14 16 18 20 22 24 3 3 6 9 12 15 18 21 24 27 30 33 36 4 4 8 12 16 20 24 28 32 36 40 44 48 5 5 10 15 20 25 30 35 40 45 50 55 60 6 6 12 18 24 30 36 42 48 54 60 66 72 7 7 14 21 28 35 42 49 56 63 70 77 84 8 8 16 24 32 40 48 56 64 72 80 88 96 9 9 18 27 36 45 54 63 72 81 90 99 108 10 10 20 30 40 50 60 70 80 90 100 110 120 11 11 22 33 44 55 66 77 88 99 110 121 132 12 12 24 36 48 60 72 84 96 108 120 132 144 Beispiel: Um 7·8 zu finden, schaut man links nach der Sieben, dann senkrecht nach der Acht. Die Antwort findet sich im Schnittpunkt der Reihe mit der Spalte und lautet 56.
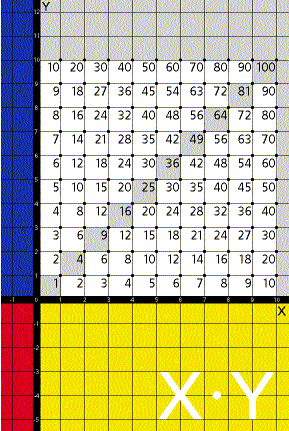
Seit Descartes' Erfindung ist die folgende Tabelle für die Grundschüler hilfreich, weil man gleichzeitig Erkenntnisse des graphischen Systems der höheren Mathematik gewinnt.
Vereinfachtes Lernen
Im kleinen Einmaleins müssen nicht alle 100 Einträge gelernt werden, die meisten Einträge sind trivial oder redundant. 45 Einträge sind doppelt vorhanden, von den verbleibenden 55 Einträgen entfallen 10 auf die Multiplikation mit 1 und (dann noch) weitere 9 auf die Multiplikation mit 10.
Weitere 8 Einträge beziehen sich auf die Multiplikation mit 5, die sehr einfach zu merken sind, ebenso wie weitere 7 auf die Multiplikation mit 2. Für die Multiplikation mit 9, die weitere 6 Einträge ausmacht, gibt es ebenso eine einfache Regel.
Es verbleiben also noch 15 Einträge, die ohne einfache Regeln auswendig gelernt werden müssen.
Der Zeitvorteil beim Anwenden der einfachen Regeln ist höher als beim klassischen Berechnen, jedoch niedriger als beim Abrufen des Auswendiggelernten. Sie werden daher als Lernhilfe eingesetzt. Der Schüler kann sich auf das Lernen der 15 Einträge ohne einfache Regeln konzentrieren. Bei der häufigen Anwendung der einfachen Regeln geschieht dann das Lernen ihrer Ergebnisse als unbewusster Vorgang, so dass der Schüler am Ende der Ausbildung das Einmaleins auswendig kennt.
Zum Erlernen des Einmaleins gibt es für Grundschüler zahlreiche Lernspiele (Wendekärtchen, Domino, LÜK-Kästen) etc. Mit dem Internet kamen auch etliche Online-Übungen.
Literatur
Das wohl bekannteste Einmaleins der Literatur ist das "Hexeneinmaleins" aus Johann Wolfgang von Goethes "Faust I".
Weblinks
Wikimedia Foundation.
