Kohärenzlänge

Die Kohärenzlänge ist der Weglängen- oder Laufzeitunterschied, den zwei Lichtstrahlen, die derselben Quelle entstammen, maximal haben dürfen, damit bei ihrer Überlagerung noch ein Interferenzmuster entsteht. Die Kohärenzlänge resultiert aus der zeitlichen Kohärenz und entspricht der optischen Weglänge, die das Licht während der Kohärenzzeit zurücklegt.

Lichtquellen mit einer großen bis sehr großen Kohärenzlänge (einige Millimeter bis viele Kilometer) sind beispielsweise Laser. Weißes Licht wie Sonnenlicht hat generell eine sehr kurze Kohärenzlänge von nur wenigen Mikrometern. Die maximale Kohärenzlänge thermischer Lichtquellen liegt bei rund 500 Millimeter, was aber nur mit speziellen Isotopenlampen zu erreichen ist. Die Kohärenzlänge modenstabilisierter HeNe-Laser kann mehrere Kilometer betragen^[1].

Anschauliche Erklärung

Unter Kohärenzlänge versteht man die Entfernung, in der man - vom letzten Phasensprung aus gemessen - die Position der Nulldurchgänge sicher vorhersagen kann. Selbstverständlich muss dazu die Wellenlänge konstant und bekannt sein.

Man kann das mit einem Beispiel aus der Kristallographie vergleichen: Wenn man bei einem Einkristall aus beispielsweise Silizium die Kristallorientierung weniger Atome des Impfkristalls und die exakten Atomabstände kennt, kann man die Position von sehr weit entfernten Atomen exakt vorhersagen. Diese sichere Distanz kann bei Silizium einige Meter betragen und entspricht der Kohärenzlänge.

Beispiel

Oben: Große Kohärenzlänge; Unten: Kurze Kohärenzlänge

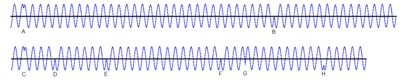
Die obere Kurve zeigt viele reguläre Schwingungen zwischen A und B. Die Wegdifferenz bei einem Interferenzversuch muss kürzer sein als die Entfernung zwischen A und B, damit Anfang und Ende dieses Schwingungszuges sich überlappen und gerade noch ein sichtbares Interferenzmuster ergeben.

Der Schwingungszug darunter besitzt eine erheblich kürzere Kohärenzlänge, auch er setzt sich aus einzelnen Schwingungszügen zusammen, die durch Phasensprünge getrennt sind. Angenommen, der Weglängenunterschied des Interferenzversuches ist genauso lang wie die Strecke D-E. Dann erzeugt dieser Wellenzug kein Muster, kürzere (wie z.B. F-G) erst recht nicht. Dagegen können E-F und G-H gerade noch Interferenzmuster erzeugen. Insgesamt wird sich ein schlecht sichtbares Muster ergeben, weil die ständig neu an beliebigen Stellen erscheinenden Interferenzmaxima (beispielsweise zwischen dem letzten Ende von E-F und dem Beginn von G-H mit undefinierter Phasenbeziehung) eine zunehmende Hintergrundhelligkeit liefern.

Es gibt einige Ursachen für endliche Kohärenzlänge:

• Kurz nach Beginn der „Sendung“ beginnt ein benachbartes Atom unabgesprochen mit einer eigenen Sendung auf der gleichen Frequenz mit anderer Phasenlage. Auch dann, wenn beide Einzelsendungen ungestört ablaufen, ergeben sich in der Summe drei Phasensprünge.

Auswirkung der Kohärenzlänge beim Doppelspaltversuch

Lichtstrahlen beim Doppelspaltversuch

Überlagerung einer Schwingung mit ihrer um Δs verschobenen Kopie

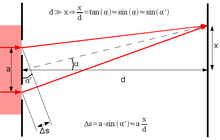
Ursache ist, dass sich die Helligkeit am rechten Messpunkt (Zielpunkt im Bild oberhalb x) kaum von der Helligkeit der Umgebung unterscheidet. Die Begründung folgt aus dem Bild darunter:

• Der obere Wellenzug relativ kurzer Kohärenzlänge erreicht den Messpunkt aus Richtung des oberen Spaltes.
• Der untere Wellenzug stammt von der gleichen Lichtquelle und besitzt die gleiche Kohärenzlänge. Er kommt aber ein wenig verspätet am Messpunkt an, weil er vom unteren Spalt kommt und deshalb einen um Δs längeren Weg zurücklegen muss.
• Würde man den Messpunkt ein wenig höher oder tiefer wählen, wäre Δs größer oder kleiner.

Am Messpunkt addieren sich die Amplituden beider Wellenzüge, dabei kann das Resultat größer oder kleiner als die Amplitude jeder Teilwelle allein werden. Die rot markierten Zeiträume im Bild bedeuten Konstruktive Interferenz, also maximale Helligkeit. Das ist wegen der geringen Kohärenzlänge nur während etwa 70 % der Gesamtzeit der Fall. Während der restlichen Zeit ist die Helligkeit am Messpunkt geringer. Dafür steigt dann die Helligkeit irgendeines benachbarten Punktes, bei dem kurzzeitig konstruktive Interferenz auftritt. Wo dieser Punkt genau liegt, hängt vom Wert des Phasensprunges ab.

Als Folge sinkender Kohärenzlänge gleichen sich die mittleren Helligkeiten aller Messpunkte an. Für sehr kurze Augenblicke kann es an jedem beliebigen Punkt konstruktive Interferenz geben und eine Folge von Bildern extrem kurzer Belichtungszeit würde chaotisch umherhüpfende Lichtpunkte zeigen. Mit steigender Kohärenzlänge werden die Verweildauern an gewissen Punkten immer länger, das bekannte Interferenzbild aus regelmäßig angeordneten hellen Punkten tritt immer deutlicher hervor. Bei unendlich großer Kohärenzlänge würde man an manchen (regelmäßig angeordneten) Messpunkten konstant große Helligkeit messen, die dazwischen liegenden Bereiche wären konstant unbeleuchtet.

Grundlagen

Interferenzsignal (3) in Abhängigkeit vom Weglängenunterschied. (2) ist die elektrische Feldstärke der Interferenz.

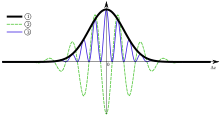
Die Abbildung rechts zeigt den Effekt der Kohärenzlänge auf ein Interferenzsignal. Kurve (3) ist die Intensität des Interferenzsignals in Abhängigkeit vom Weglängenunterschied. Die Kohärenzlänge ist in dieser Darstellung die Breite der Einhüllenden Kurve (1) bei halber Amplitude.

Der Zusammenhang zwischen Kohärenzlänge l_c und Kohärenzzeit τ_c ist durch folgende Gleichung gegeben:

$l_c = \tau_c \cdot c = \tau_c \cdot \frac {c_0}{n}$

Dabei ist c₀ die Lichtgeschwindigkeit im Vakuum und n die Brechzahl des umgebenden Mediums.

Anwendungen

Sowohl große als auch kleine Kohärenzlängen finden in unterschiedlichen optischen Messverfahren Anwendung. Große Kohärenzlängen werden in Laserinterferometern eingesetzt, die besonderen Eigenschaften einer kleinen Kohärenzlänge werden im Weißlichtinterferometer ausgenutzt.

Siehe auch

• Interferometrie
• Kohärenz

Anmerkungen

1. ↑ Speckle-Interferometrie mit einem Mach-Zehnder-Interferometer