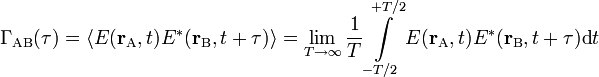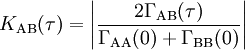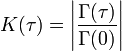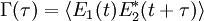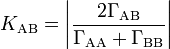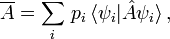- Kohärenzzeit
-
Kohärenz (v. lat.: cohaerere = zusammenhängen) bezeichnet in der Physik eine Eigenschaft von Wellen, die stationäre (zeitlich und räumlich unveränderliche) Interferenzerscheinungen ermöglicht. Allgemeiner beschreibt die Kohärenz die Gesamtheit der Korrelationseigenschaften zwischen Größen eines Wellenfeldes.
Nähere Beschreibung
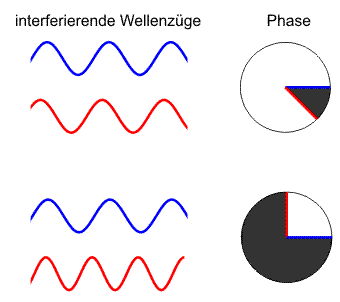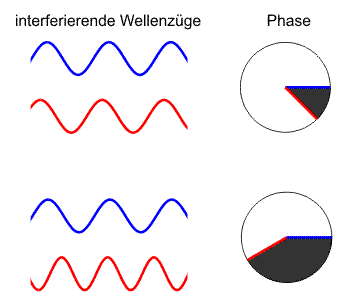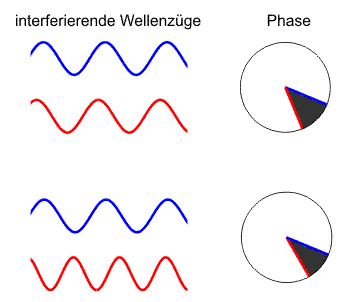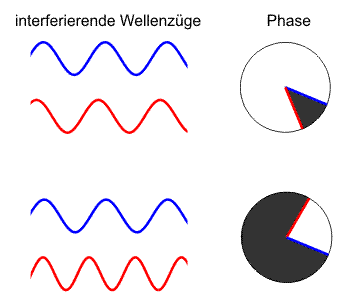 Zeigerdiagramm mit Phasen und Phasendifferenz (schwarz) zweier Wellenzüge. Oben: kohärente Wellenzüge mit konstanter Phasendifferenz; Unten: inkohärente Wellenzüge ohne feste Phasenbeziehung.
Zeigerdiagramm mit Phasen und Phasendifferenz (schwarz) zweier Wellenzüge. Oben: kohärente Wellenzüge mit konstanter Phasendifferenz; Unten: inkohärente Wellenzüge ohne feste Phasenbeziehung.Damit bei Überlagerungen bestimmter Teilwellen Interferenzphänomene beobachtet werden können, müssen die Zusammensetzungen dieser Wellen bestimmte Bedingungen erfüllen, die mit Kohärenz zusammengefasst werden. Zwei Wellen sind kohärent, wenn sie eine feste Phasenbeziehung haben, im anderen Fall inkohärent.
 links: räumlich und zeitliche kohärente Welle - die Phase ist sowohl in zeitlicher Richtung als auch in räumlicher Richtung ohne Sprünge und vollkommen vorhersagbar. Mitte: ausschließlich räumliche Kohärenz - entlang der Zeitachse springt die Phase der Welle unvorhersagbar. Rechts: ausschließlich zeitliche Kohärenz - entlang der Raumachse springt die Phase der Welle unvorhersagbar.
links: räumlich und zeitliche kohärente Welle - die Phase ist sowohl in zeitlicher Richtung als auch in räumlicher Richtung ohne Sprünge und vollkommen vorhersagbar. Mitte: ausschließlich räumliche Kohärenz - entlang der Zeitachse springt die Phase der Welle unvorhersagbar. Rechts: ausschließlich zeitliche Kohärenz - entlang der Raumachse springt die Phase der Welle unvorhersagbar.In der Natur auftretende Wellen, seien es Lichtwellen, Schallwellen oder Wasserwellen, können aus verschiedenen Frequenzanteilen, Phasen und Ausbreitungsrichtungen zusammengesetzt sein. Eine Möglichkeit diese Zusammensetzung zu interpretieren ist Folgende: Jeweils zwei Teilwellen können zu einander kohärent sein, wie oben dargestellt, und ein zeitlich stabiles Interferenzmuster erzeugen. Alle diese Interferenzmuster (Intensitäten) überlagern sich auf dem Beobachtungsschirm und können sich entweder gegenseitig verstärken (vollständige Kohärenz), teilweise auslöschen (partielle Kohärenz) oder vollständig zu einer mittleren Intensität auslöschen (Inkohärenz).
Außerdem kann man die Fälle einer zeitlichen und einer räumlichen Kohärenz unterscheiden, auch wenn in fast allen Versuchen beide Formen der Kohärenz vorhanden sein müssen. Zeitliche Kohärenz liegt vor, wenn entlang der Zeitachse (oft bildlich gleichgesetzt mit der Raumachse parallel zur Ausbreitungsrichtung) eine feste Phasendifferenz (ohne Sprünge) besteht, räumliche Kohärenz liegt vor, wenn entlang einer Raumachse (oft reduziert auf die Raumachse senkrecht zur Ausbreitungsrichtung) eine feste Phasendifferenz besteht.
Mathematische Darstellung
Kohärenz und Korrelation
Die Kohärenz von Wellen kann anhand der Korrelationsfunktion quantifiziert werden. Diese Funktion liefert ein Maß für die Ähnlichkeit des zeitlichen Verlaufs zweier in Verbindung gebrachten Wellenamplituden.
Die Funktion
definiert zunächst die (komplexe) Kreuzkorrelationsfunktion zwischen den Zeitverläufen zweier betrachteter Amplituden. Die beiden Amplituden werden an den Ortspunkten A und B der Welle E und bei einem Zeitunterschied von τ herausgegriffen und als Funktion der Zeit verglichen.
Die Kontrastfunktion für raumzeitliche Kohärenz, die durch
gegeben ist, liefert nun direkt die Stärke der Kohärenz als Wert zwischen 0 und 1. Im Allgemeinen unterscheidet man drei Fälle:
KAB(τ) = 1 vollständige Kohärenz 0 < KAB(τ) < 1 partielle Kohärenz KAB(τ) = 0 vollständige Inkohärenz Im Falle rein zeitlicher Kohärenz werden nur Korrelationen mit A=B betrachtet. Hier liefert die Kontrastfunktion für zeitliche Kohärenz
die Stärke der zeitlichen Kohärenz in Abhängigkeit des Zeitabstandes τ. K(τ) hat bei τ = 0 den maximalen Wert 1 und fällt je nach Kohärenz mehr oder weniger schnell auf 0 ab. Die Kohärenzzeit τc ist definiert als der Zeitabstand τ, bei dem die Kontrastfunktion auf 1/e abgefallen ist. Soll die Kohärenz zwischen verschiedenen Wellen berechnet werden, wird die Kreuzkorrelationsfunktion
der Wellen E1 und E2 verwendet.
Im Falle rein räumlicher Kohärenz werden nur Korrelationen mit τ = 0 betrachtet. Hier liefert die Kontrastfunktion für räumliche Kohärenz
die Stärke der räumlichen Kohärenz zwischen den Punkten A und B. Ein Volumen, in dem alle Punktepaare A, B einen Kontrast KAB > 1 / e aufweisen, bildet ein sogenanntes Kohärenzvolumen innerhalb dem räumliche Kohärenz vorliegt. Meist wird unter dem Begriff räumliche Kohärenz nur die Kohärenz quer zur Ausbreitungsrichtung der Welle verstanden, was präziser mit transversal räumlicher Kohärenz bezeichnet werden müsste. Die räumliche Kohärenz entlang der Ausbreitungsrichtung, also die longitudinal räumliche Kohärenz wird dagegen oft mit der zeitlichen Kohärenz gleichgesetzt, was nicht ganz korrekt ist.
Kohärenz in der klassischen Optik
In der klassischen Optik wird Kohärenz mit der Interferenzfähigkeit von Licht in direkten Zusammenhang gebracht. Der Kontrast des Interferenzmusters ist ein Maß für die Kohärenz des Lichts. Insbesondere in der Optik spielen die beiden Spezialfälle der räumlichen und zeitlichen Kohärenz eine große Rolle.
Kohärenz und Kontrast eines Interferogramms
In der Optik bedeutet Kohärenz die Interferenzfähigkeit bezüglich eines bestimmten Experimentes und wird mit dem Kontrast V des Interferenzmusters, der maximal 1 (vollständig kohärentes Licht) und minimal 0 (vollständig inkohärentes Licht) sein kann, in Verbindung gebracht. Das Interferenzmuster zweier Lichtquellen ist abhängig von ihrer komplexen gegenseitigen Kohärenzfunktion
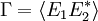 bzw. dem komplexen gegenseitigen Kohärenzgrad
bzw. dem komplexen gegenseitigen Kohärenzgrad 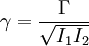 , bzw. vom Kontrast
, bzw. vom Kontrast 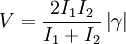
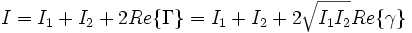
Für Zweistrahlinterferenz einer Welle
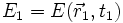 mit ihrer räumlich und zeitlich verschobenen Kopie
mit ihrer räumlich und zeitlich verschobenen Kopie 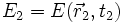 ergibt sich die bekannte Zweistrahlinterferenzformel
ergibt sich die bekannte Zweistrahlinterferenzformel 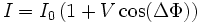
Zeitliche Kohärenz
Licht entsteht aus diskontinuierlichen Emissionsakten, die Photonen-Wellenzüge aussenden. Diese Wellenzüge sind jeweils mit einem regelmäßig oszillierenden Feld verbunden, das willkürlich seine Phase verändert. "Dieses Intervall, in dem die Lichtwelle eine Sinusschwingung darstellt, ist ein Maß für ihre zeitliche Kohärenz."[1] Die Kohärenzzeit ist somit durch das durchschnittliche Zeitintervall definiert, indem die Lichtwelle in einer vorhersagbaren Weise schwingt. Mit der Kohärenzzeit steigt auch die zeitliche Kohärenz einer Licht emittierenden Quelle.
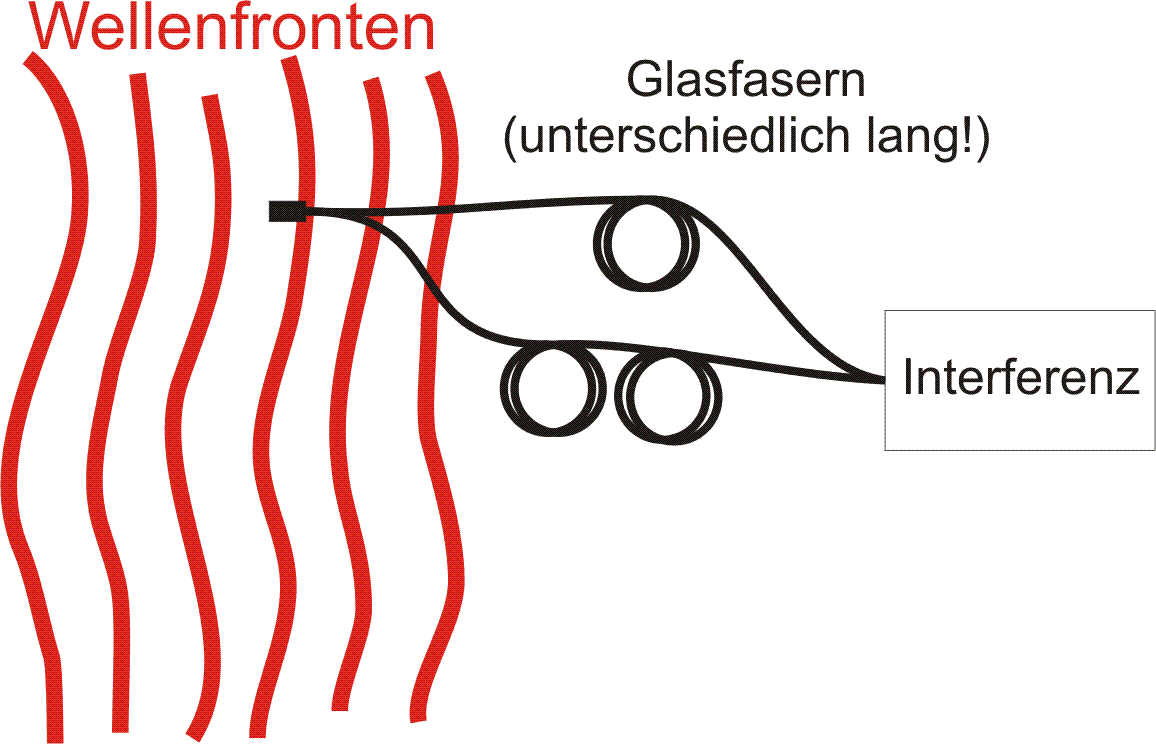
Zeitliche Kohärenz ist dann nötig, wenn die Welle zu einer zeitlich verschobenen Kopie ihrer selbst kohärent sein soll. Das ist beispielsweise dann der Fall, wenn in einem Michelson-Interferometer die Weglängen im Objekt- und Referenzarm unterschiedliche Längen aufweisen. Die Zeit, nach der sich relativ die Phasenlage oder Amplitude signifikant verändert hat (so dass die Korrelation in entscheidendem Maße abnimmt) ist als die Kohärenzzeit τc definiert. Bei Δt = 0 ist die Kohärenz noch perfekt, sie hat sich aber nach der Zeit Δt = τc entscheidend verringert. Die Kohärenzlänge lc ist als die Entfernung definiert, die die Welle innerhalb der Kohärenzzeit zurücklegt.
Wiener-Chintschin-Theorem
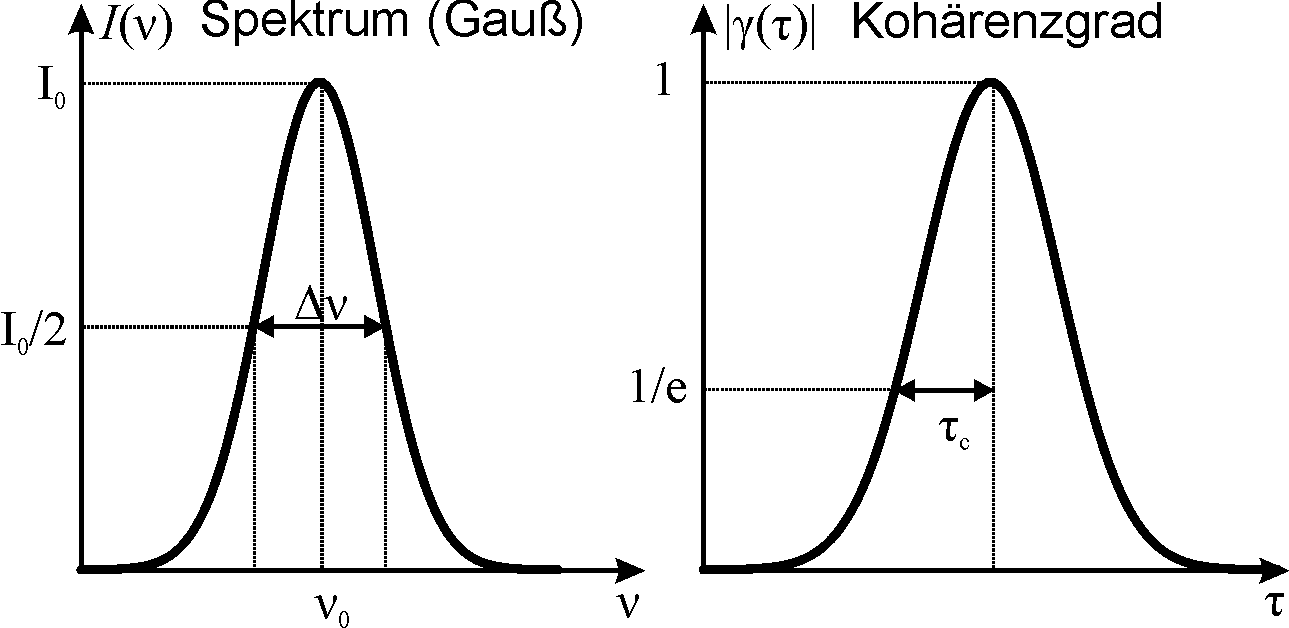
Bei einer Lichtquelle wird die zeitliche Kohärenz durch die spektrale Zusammensetzung des Lichts bestimmt. Licht einer monochromatischen Lichtquelle ist zeitlich vollständig kohärent. Licht, das sich aus verschiedenen Wellenlängen zusammensetzt (z. B. wegen Dopplerverbreiterung), ist – je nach Art der Zusammensetzung – partiell kohärent oder inkohärent. Dieser Zusammenhang wird durch das Wiener-Chintschin-Theorem beschrieben, das besagt, dass der Kohärenzgrad (als Autokorrelationsfunktion der Feldstärke) der normierten Fouriertransformation des Lichtspektrums entspricht. Die Kohärenzlänge des Lichts ist als der Punkt definiert, an dem der Kohärenzgrad auf 1 / e abgefallen ist.
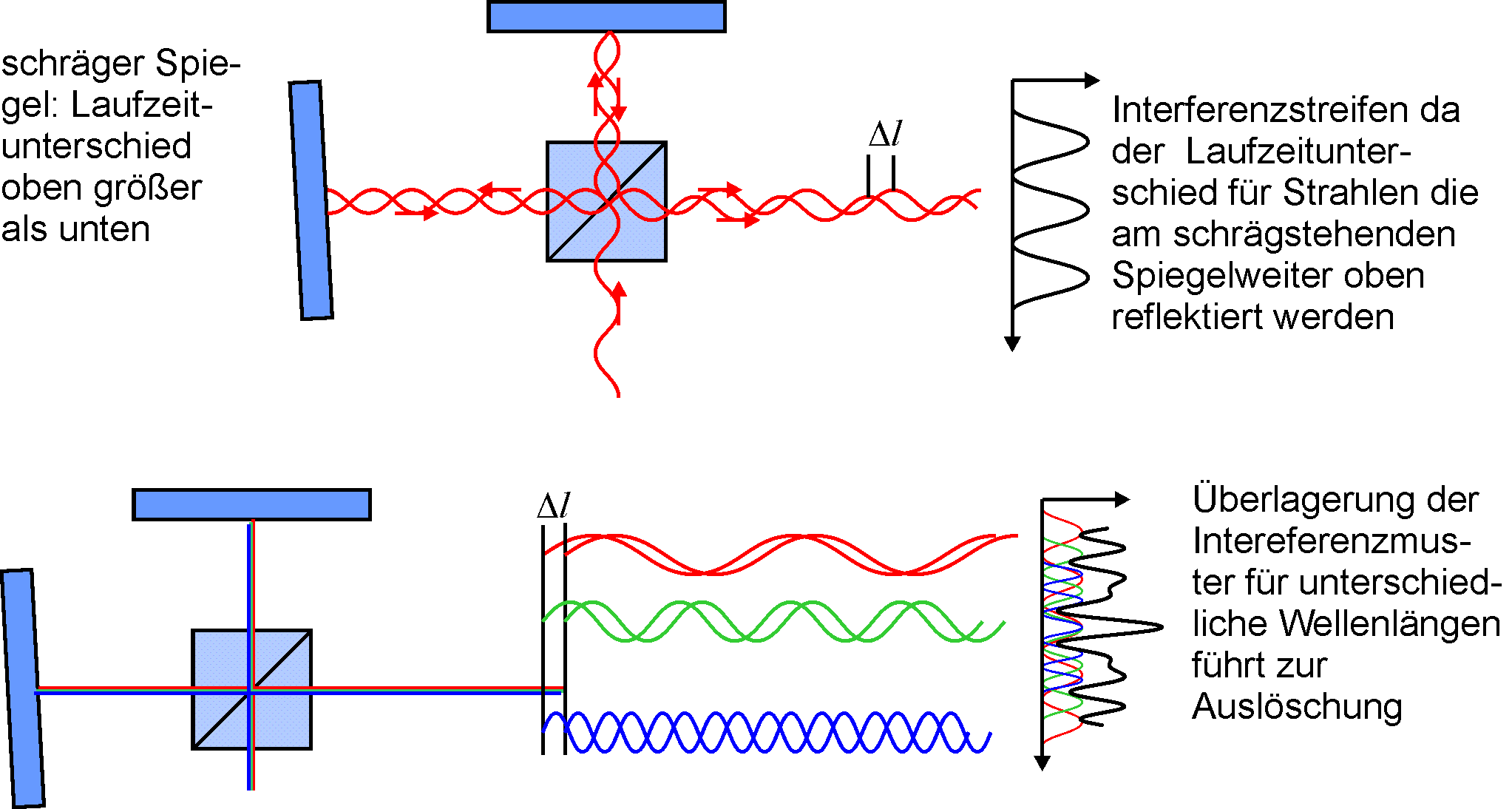
Den Zusammenhang zwischen dem Spektrum der Lichtquelle und der zeitlichen Kohärenz kann man sich am Beispiel des Michelson-Interferometers veranschaulichen. Bei verkipptem Referenzspiegel ist der Weglängenunterschied beider Strahlen linear von der Kipprichtung abhängig. Entspricht der Weglängenunterschied einem ganzzahligen Vielfachen der Wellenlänge, so interferieren die Strahlen konstruktiv, und das Interferenzmuster hat ein Maximum. Bei monochromatischem Licht ist ein Streifenmuster auf dem Schirm sichtbar.
Besteht das Licht aus verschiedenen Wellenlängen, so sind die einzelnen Streifenmuster zu einander verschoben. Die Streifen sind umso breiter, je größer die Wellenlänge ist. Bei der Überlagerung der Streifenmuster auf einem Beobachtungsschirm löschen sich die Streifen an manchen Orten gegenseitig aus oder verstärken sich gegenseitig (partielle Kohärenz). Die Wiederkehr des Kontrasts ist im Bild der endlich langen Wellenzüge nicht erklärbar.
Berechnet nach dem Wiener-Chintschin-Theorem die Kohärenzfunktion für den Fall eines Lasers mit einem gaußförmigen Spektrum (Bandbreite FWHM = Δλ, Schwerpunktwellenlänge λ), so erhält man eine gaußförmige Kohärenzfunktion mit der Kohärenzlänge
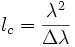 .
.Aus der Fouriertransformation folgt direkt, dass – je nach Form des Spektrums (im obigen Fall des gaußförmigen Spektrums beispielsweise nicht) – auch für größere Weglängenunterschiede als lc wieder eine hohe Kohärenz erreicht werden kann. Diese Eigenschaft der Kohärenz lässt sich im anschaulichen Bild der endlich langen Wellenzüge (s.u.) nicht erklären.
Anschauliche Erklärung der zeitlichen Kohärenz durch endliche Wellenzüge
„Natürliches“ Licht entsteht, wenn ein Elektron in einem Atom von einem angeregten in einen weniger angeregten Zustand übergeht. Beim Zerfall des angeregten Zustandes schwingt in semiklassischer Vorstellung das Elektron eine gewisse Zeit. Während dieser Zeit (= Lebensdauer) wird es ein Photon emittieren (gedämpfte Schwingung). Typische Lebensdauern solcher atomarer Prozesse sind
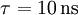 (= Kohärenzzeit). Dies führt zu Wellenpaketen mit Längen von
(= Kohärenzzeit). Dies führt zu Wellenpaketen mit Längen von 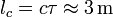 (= Kohärenzlänge) mit einer Frequenzunschärfe
(= Kohärenzlänge) mit einer Frequenzunschärfe 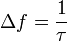 von etwa 20 MHz. Da die Atome im Allgemeinen in thermischer Bewegung sind, zeigt das Licht, das von (vielen) solchen Atomen emittiert wird, Dopplerverbreiterung, bei starker gegenseitiger Wechselwirkung (z. B. Stöße) der Atome auch Stoßverbreiterung. Beide Effekte verkürzen die Kohärenzzeit bzw. -länge des emittierten Lichts erheblich.
von etwa 20 MHz. Da die Atome im Allgemeinen in thermischer Bewegung sind, zeigt das Licht, das von (vielen) solchen Atomen emittiert wird, Dopplerverbreiterung, bei starker gegenseitiger Wechselwirkung (z. B. Stöße) der Atome auch Stoßverbreiterung. Beide Effekte verkürzen die Kohärenzzeit bzw. -länge des emittierten Lichts erheblich.Das Modell der endlichen Wellenzüge kann nicht alle Aspekte der zeitlichen Kohärenz erklären! Es dient daher nur als Hilfsvorstellung in sehr einfachen Fällen.
Räumliche Kohärenz
Soll die Welle mit einer räumlich verschobenen Kopie ihrer Selbst interferieren, ist räumliche Kohärenz nötig. Dies ist beispielsweise im youngschen Doppelspaltversuch der Fall: Hier werden durch die beiden Spalte zwei Punkte aus der einfallenden Welle herausgegriffen, und zur Interferenz gebracht. Wie weit diese beiden Punkte auseinander liegen dürfen, beschreibt die Ausdehnung des Gebiets der räumlichen Kohärenz.
van-Cittert-Zernike-Theorem
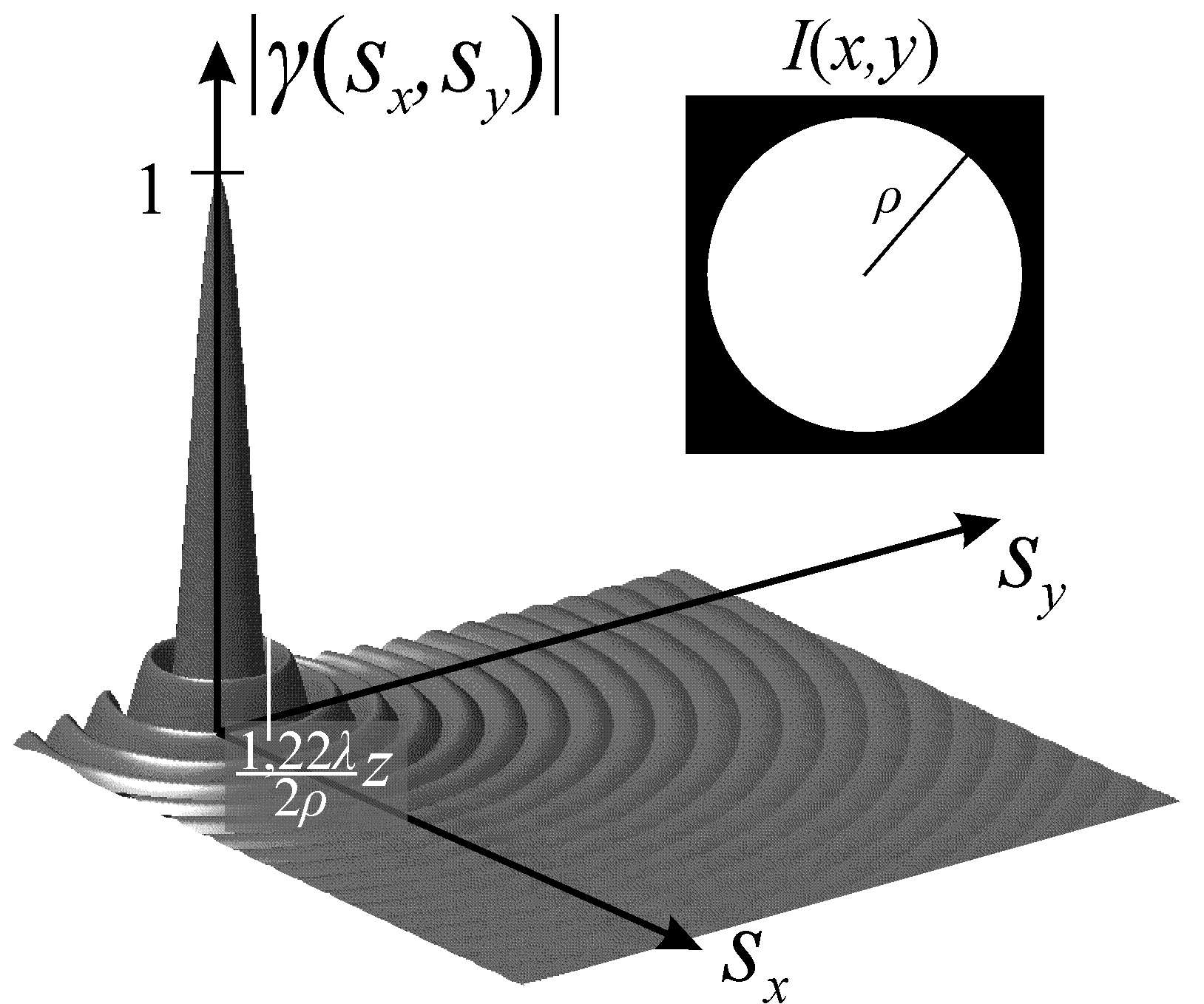
Bei einer ausgedehnten Lichtquelle mit statistischer Phasenverteilung (d.h. LED, Glühbirne, Gasentladungslampe; für Laser nicht zutreffend) wird die räumliche Kohärenz durch die Ausdehnung und die Form der Lichtquelle bestimmt. Dabei geht es mehr um die Winkelausdehnung als um die tatsächliche Ausdehnung, so dass die räumliche Kohärenz daher mit steigender Entfernung zunimmt. Eine Punktlichtquelle hat auch bei geringem Abstand eine vollständige räumliche Kohärenz. Dieser Zusammenhang wird durch das van-Cittert-Zernike-Theorem beschrieben, das besagt, dass der komplexe Kohärenzgrad der normierten Fouriertransformierten der Intensitätsverteilung der Lichtquelle entspricht (Bedingungen: kleine Ausdehnungen der Lichtquelle und des Beobachtungsgebiets, ausreichend großer Beobachtungsabstand). Für eine kreisförmige Lichtquelle fällt die räumliche Kohärenz schnell ab und erreicht bei 1,22λz / 2ρ ihr Minimum in Abhängigkeit vom Abstand z des Beobachtungsschirms von der Lichtquelle. Danach ist die Kohärenz nicht verloren, sondern kommt für größere Abstände (in sehr schwacher Form) wieder.
Den Zusammenhang zwischen Ausdehnung der Lichtquelle und räumlicher Kohärenz kann man sich am Beispiel des Doppelspalt-Interferenzversuchs veranschaulichen. Am Beobachtungsschirm entsteht abhängig von den Laufzeitunterschieden der beiden Strahlen ein Interferenzmuster. Hierfür ist eine ausreichend hohe zeitliche Kohärenz der Lichtstrahlen nötig. Für den Punkt des Beobachtungsschirms, der zwischen den beiden Spalten liegt, haben die Lichtstrahlen keine Laufzeitdifferenz. Hier hat das Interferenzmuster das nullte Maximum. Bei einer ausgedehnten Lichtquelle ist der Punkt mit Laufzeitdifferenz = 0 für jeden Punkt der Lichtquelle leicht verschoben. Die einzelnen Interferenzmuster verwischen sich je nach Größe der Lichtquelle gegenseitig.
Erzeugung von kohärentem Licht
Kohärenz ist keine Eigenschaft einer Lichtquelle, sondern der Lichtstrahlen, da sich die Interferenzfähigkeit des Lichts bei seiner Ausbreitung ändern kann.
Wenn man räumlich nicht-kohärentes Licht durch einen sehr schmalen Spalt sendet, verhält sich das Licht dahinter, als sei der Spalt eine Punktlichtquelle (in einer Dimension), die Elementarwellen aussendet (siehe Huygenssches Prinzip). Die Größe des räumlichen Kohärenzgebiets ist im Fall eines einfachen Spaltes indirekt proportional zur Spaltgröße (van-Cittert-Zernike-Theorem, Verdetsche Kohärenzbedingung). Mit zunehmendem Abstand zur Lichtquelle nimmt die Winkelausdehnung der Lichtquelle ab und damit die räumliche Kohärenz zu.
Die zeitliche Kohärenz des Lichts kann erhöht werden, indem man einen Wellenlängenfilter einsetzt, der das Spektrum der Lichtquelle begrenzt.
Die Wahl der Lichtquelle ist daher entscheidend für die Kohärenz. Leuchtstoffröhren, Glühlampen und Gasentladungslampen sind räumlich ausgedehnte Lichtquellen (räumlich inkohärent), die weißes Licht einer großen Menge verschiedener Frequenzen (zeitlich inkohärent) erzeugen. Durch Lochblenden und Wellenlängenfilter kann daraus räumlich und zeitlich kohärentes Licht erzeugt werden, jedoch wird dabei die verbleibende Intensität des Lichts stark reduziert, so dass dieses Verfahren wenig praktikabel ist.
Laserlicht dagegen gilt als das am besten erzeugbare monochromatische Licht überhaupt und hat die größte Kohärenzlänge (bis zu mehreren Kilometern). Ein Helium-Neon-Laser kann beispielsweise Licht mit Kohärenzlängen von über 1 km produzieren. Allerdings sind nicht alle Laser monochromatisch (z. B. Titan-Saphir-Laser Δλ ≈ 2 nm – 70 nm). LEDs sind weniger monochromatisch (Δλ ≈ 300 nm) und haben deshalb kürzere Kohärenzzeiten als die meisten monochromatischen Laser. Da ein Laser über seine gesamte Apertur dieselbe Phase hat, besitzt Laserlicht zudem eine sehr hohe räumliche Kohärenz.
Messung der Kohärenz
Zeitliche Kohärenz
Man kann die Kohärenzzeit bzw. Kohärenzlänge einer Lichtwelle bestimmen, indem man diese in zwei Teilstrahlen aufteilt und sie später wieder vereint – etwa in einem Michelson-Interferometer oder Mach-Zehnder-Interferometer. Man sieht Interferenzerscheinungen in einer solchen Anordnung nur dann, wenn der Laufzeitunterschied bzw. der Wegunterschied zwischen den Teilwellen kleiner bleibt als die Kohärenzzeit bzw. Kohärenzlänge der von den Atomen ausgesandten Wellenzügen.
Auch aus der Messung des Spektrums lässt sich durch Fouriertransformation die zeitliche Kohärenz bestimmen. Umgekehrt kann auch das Spektrum einer Lichtquelle bestimmt werden, indem der Interferenz-Kontrast in einem Michelson-Interferometer gemessen wird, während der Weglängenunterschied variiert wird (Fourier-Spektroskopie).
Räumliche Kohärenz
Ähnlich wie im Fall der zeitlichen Kohärenz kann die räumliche Kohärenz durch Messung des Kontrastes eines Interferenzmusters bestimmt werden, wenn ein Interferometer eingesetzt wird, das empfindlich auf die räumliche Kohärenz ist (Verwandte des Doppelspaltaufbaus). Bei der Stellarinterferometrie wird durch Messung des Kontrasts über die räumliche Kohärenz die Winkelausdehnung von Sternen bestimmt.
Anwendungen
Holographie
Bei den Anwendungen optisch-kohärenter Superposition muss unbedingt die Holographie erwähnt werden, die in einem Spezialartikel behandelt wird, dem nichts hinzuzufügen ist. Es handelt sich um ein besonders aktuelles Gebiet für wichtige Bereiche des täglichen Lebens (z. B. Banknoten, Chipkarten).
Nicht-optische Wellenfelder
Weitere Anwendungen betreffen die kohärente bzw. inkohärente Superposition nicht-optischer Wellenfelder. In der Quantenmechanik geht es beispielsweise um ein Wahrscheinlichkeitsfeld, das mit der Wellenfunktion
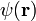 zusammenhängt (Bedeutung: Wahrscheinlichkeitsamplitude). Dies betrifft zukünftige Anwendungen wie das Quantum Computing oder die bereits gegenwärtig mögliche Quantenkryptographie. U.a. geht es um das in folgendem Unterkapitel besprochene grundsätzliche Problem:
zusammenhängt (Bedeutung: Wahrscheinlichkeitsamplitude). Dies betrifft zukünftige Anwendungen wie das Quantum Computing oder die bereits gegenwärtig mögliche Quantenkryptographie. U.a. geht es um das in folgendem Unterkapitel besprochene grundsätzliche Problem:Kohärente vs. inkohärente Superposition in Quantenmechanik und statistischer Physik
Mit kohärenter Superposition der Zustände (Superposition der Feldamplituden) hat man es auch in der Quantenmechanik zu tun, obwohl der Zusammenhang mit den Messgrößen kompliziert ist: Ein quantenmechanischer Zustandsvektor
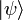 , interpretiert als Ensemble von Wahrscheinlichkeitsamplituden (genauer: deren Dichten), die durch eine komplexwertige Ortsfunktion
, interpretiert als Ensemble von Wahrscheinlichkeitsamplituden (genauer: deren Dichten), die durch eine komplexwertige Ortsfunktion 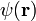 dargestellt werden, kann in einer beliebigen Orthonormalbasis
dargestellt werden, kann in einer beliebigen Orthonormalbasis 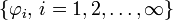 mit komplexen Konstanten ci linear superponiert werden, obwohl die Messwahrscheinlichkeiten selbst quadratisch von ψ abhängen (z. B. gilt für die Aufenthaltwahrscheinlichkeit w(dV) in einem kleinen Volumen dV die folgende Aussage:
mit komplexen Konstanten ci linear superponiert werden, obwohl die Messwahrscheinlichkeiten selbst quadratisch von ψ abhängen (z. B. gilt für die Aufenthaltwahrscheinlichkeit w(dV) in einem kleinen Volumen dV die folgende Aussage: 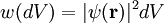 ). Die lineare Superponierbarkeit besagt, dass zugleich
). Die lineare Superponierbarkeit besagt, dass zugleich 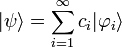 gilt, also
gilt, also 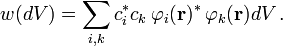 (Der Index * kennzeichnet bei den Physikern die konjugiert-komplexe Größe.) Die Aufenthaltswahrscheinlichkeit hängt also quadratisch (genauer: bilinear) von den
(Der Index * kennzeichnet bei den Physikern die konjugiert-komplexe Größe.) Die Aufenthaltswahrscheinlichkeit hängt also quadratisch (genauer: bilinear) von den 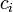 ab, obwohl die Zustände selbst linear (d.i. kohärent) superponiert werden. Die hier besprochenen Aspekte werden beim Quantum Computing ausgenutzt.
ab, obwohl die Zustände selbst linear (d.i. kohärent) superponiert werden. Die hier besprochenen Aspekte werden beim Quantum Computing ausgenutzt.Allgemein ist der quantenmechanische Erwartungswert einer Messgröße A, die durch einen sog. selbstadjungierten Operator
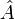 repräsentiert wird, durch folgende Formel gegeben (wobei die Ausdrücke in spitzen Klammern das quantenmechanische Skalarprodukt bedeuten, worauf an dieser Stelle nicht eingegangen werden kann):
repräsentiert wird, durch folgende Formel gegeben (wobei die Ausdrücke in spitzen Klammern das quantenmechanische Skalarprodukt bedeuten, worauf an dieser Stelle nicht eingegangen werden kann): 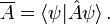 Obwohl dieser Ausdruck nichtlinear von ψ abhängt, ist die kohärente Superponierbarkeit der Zustände das Wesentliche: auch die nichtdiagonalen Elemente,
Obwohl dieser Ausdruck nichtlinear von ψ abhängt, ist die kohärente Superponierbarkeit der Zustände das Wesentliche: auch die nichtdiagonalen Elemente, 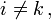 geben einen signifikanten Beitrag zum Resultat.
geben einen signifikanten Beitrag zum Resultat.Dagegen ist in der statistischen Physik, einschließlich der Quantenstatistik, die Mittelung von vornherein inkohärent (Superposition von Feldintensitäten). Hier wird mit Wahrscheinlichkeiten pi angenommen, dass sich der quantenmechanische Zustand des Systems im Zustand
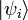 befindet. Die statistischen Erwartungswerte sind dementsprechend
befindet. Die statistischen Erwartungswerte sind dementsprechendmit
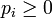 und
und 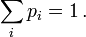
Es werden also eigentlich nicht die Zustände, sondern die Erwartungswerte selbst, d.h. die "Intensitäten", superponiert und Nichtdiagonalelemente treten nicht auf. Die zugehörige Entropie - eine wichtige physikalische und informationstheoretische Größe - verschwindet folglich nicht. (Dagegen sind quantenmechanische Zustände "rein" im folgenden Sinne:
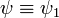 , d.h.
, d.h. 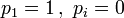 für
für 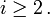 Die Entropie verschwindet jetzt.)
Die Entropie verschwindet jetzt.)Statistische Methoden, auf denen z. B. die Signalverstärkung am Ende einer Glasfaser beruht, sind also schädlich für die Kohärenz, was u.a. zur Reichweitenbegrenzung der Quantenkryptographie führt, die gegenwärtig nur auf Abständen bis zu ca. 100 km durchgeführt werden kann, während die Methoden der klassischen Informatik in ihrer Reichweite praktisch unbegrenzt sind.
Quellen
- ↑ Eugene Hecht: Optik. 4., überarbeitete Auflage Auflage. 2005, S. 631.
Siehe auch
Weblinks
- Die „Vorlesung Physik III, 59. Stunde“ beinhaltet eine verständliche Erklärung zum Thema Interferenz und Kohärenz
- Kohärenz und Korrelation in der Tonstudiotechnik
- Kohärenz von Licht - PPP aus der Reihe Karlsruher Physikkurs von Gerhard Anzt
Literatur
- Paul, Harry: Lexikon der Optik, Spektrum Akademischer Verlag, 2003, ISBN 3-8274-1422-9
- Lauterborn, Werner: Kohärente Optik. Grundlagen für Physiker und Ingenieure, Springer 1993, ISBN 3-540-56769-0
- Lipson, Lipson, Tannhauser: Optik, Springer 1997, ISBN 3-540-61912-7
- Goodman, Joseph: Statistical Optics, Wiley 1985, ISBN 0-471-01502-4
Wikimedia Foundation.