- Kombinatorische Explosion
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Kombinatorik ist ein Teilgebiet der Mathematik, das sich mit der Bestimmung der Zahl möglicher Anordnungen oder Auswahlen von
- unterscheidbaren oder nicht unterscheidbaren Objekten
- mit oder ohne Beachtung der Reihenfolge
beschäftigt. In der modernen Kombinatorik werden diese Probleme umformuliert als Abbildungen, sodass sich die Aufgabe der Kombinatorik im wesentlichen darauf beschränken kann, diese Abbildungen zu zählen.
Für das Rechnen mit Wahrscheinlichkeiten auf der Basis des Wahrscheinlichkeitsbegriffs von Laplace bildet die Kombinatorik eine wichtige Grundlage.
Ein verblüffendes Phänomen der Kombinatorik ist, dass sich oftmals wenige Objekte auf vielfältige Weise kombinieren lassen. Beim Zauberwürfel können beispielsweise die 26 Elemente auf rund 43 Trillionen Arten kombiniert werden. Dieses Phänomen wird oft als kombinatorische Explosion bezeichnet und ist auch die Ursache für das so genannte Geburtstagsparadoxon.
Inhaltsverzeichnis
Anordnungen (Permutationen)
Permutation: „Jede mögliche Anordnung von n Elementen, in der alle Elemente verwendet werden, heißt Permutation dieser Elemente.“
Unterscheidbare Objekte mit Beachtung der Reihenfolge
Als einführendes Beispiel mag die Zahl der Anordnungen von sechs unterscheidbaren Objekten mit Beachtung der Reihenfolge dienen. Offensichtlich kann jedes der Objekte „auf den ersten Platz gelangen“, es gibt also sechs Möglichkeiten, den ersten Platz zu besetzen. Wenn der erste Platz besetzt ist, bleiben noch fünf Kandidaten für den zweiten Platz, ist auch dieser besetzt, nur noch vier Kandidaten für den dritten Platz, und so fort. Für den vorletzten Platz bleiben schließlich nur noch zwei Objekte übrig, und der letzte Platz muss mit dem übriggebliebenen Objekt besetzt werden.
Es gilt: Die Anzahl der Permutationen von n verschiedenen Elementen ist n!. Das Ausrufezeichen steht für „Fakultät“ und wird auch so gelesen, also „n Fakultät“.
Wenn den Kandidaten feste Plätze zugeordnet werden, und man wissen möchte, wieviele Möglichkeiten existieren, so dass sich kein einziger Kandidat auf seinen vorgesehenen Platz setzt, berechnet man das über die Subfakultät !n. Bei sechs Kandidaten sind das !6 = 265 Möglichkeiten.
- Beispiel
- Es gibt 6·5·4·3·2·1 oder 6! = 720 Möglichkeiten, sechs unterscheidbare Objekte anzuordnen.
- Es gibt 32! Möglichkeiten die 32 Spielkarten eines Blattes anzuordnen (ca.
 )
)
Objekte mehrerer Klassen mit Beachtung der Reihenfolge
Für die Zahl der möglichen Anordnungen von Objekten aus mehreren Klassen, die untereinander jeweils innerhalb einer Klasse nicht unterscheidbar sind, ist es hilfreich, zunächst die mögliche Zahl der Anordnungen der Objekte zu betrachten und dann zu überlegen, wieviele dieser Anordnungen nicht unterscheidbar sind. Die Zahl der möglichen Anordnungen bei unterscheidbaren Objekten wird durch die Zahl der nicht unterscheidbaren Anordnungen geteilt.
Wenn die mögliche Zahl von Anordnungen von zwei Objekten einer ersten Klasse, drei Objekten einer zweiten Klasse und fünf Objekten einer dritten Klasse ermittelt werden soll, dann gibt es zunächst (2 + 3 + 5)! oder 3.628.800 mögliche Anordnungen. Weil aber Anordnungen nicht unterscheidbar sind, bei denen nur Objekte einer Klasse untereinander den Platz getauscht haben, weil also jeweils 2! · 3! · 5! oder 1.440 der möglichen Anordnungen gleich erscheinen, gibt es nur 3.628.800/1.440 oder 2.520 unterscheidbare Anordnungen dieser Elemente. Allgemein:
- Anzahl der Permutationen von n Elementen, die in k Gruppen von je l1,l2,...,lk gleichen Elementen mit
 fallen:
fallen: 
Auswählen mit Beachtung der Reihenfolge (Variationen)
Variation ohne Zurücklegen
Bei der Variation ohne Zurücklegen sollen n Plätze mit jeweils einem von k Objekten besetzt werden. Jedes Objekt kann dabei höchstens einen Platz einnehmen. Es muss also
 gelten. Hier gibt es
gelten. Hier gibt esMöglichkeiten. Die Notationen
 und (n)k werden als fallende Faktorielle bezeichnet.
und (n)k werden als fallende Faktorielle bezeichnet.Mengendarstellung: Die Menge
 ist die Menge aller Variationen ohne Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Variationen ohne Wiederholung von n Dingen zur Klasse k (für  ). Sie heißt auch Menge aller Permutationen ohne Wiederholung von n Dingen zur Klasse k. Sie hat die oben angegebene Anzahl von Elementen.
). Sie heißt auch Menge aller Permutationen ohne Wiederholung von n Dingen zur Klasse k. Sie hat die oben angegebene Anzahl von Elementen.Variation mit Zurücklegen
Wenn aus n Objekten k Objekte mit Zurücklegen und mit Beachtung der Reihenfolge ausgewählt werden sollen, dann kann jedes der n Objekte auf jedem der k Plätze der Auswahl erscheinen, es gibt demzufolge
- nk mögliche Auswahlen.
Mengendarstellung: Die Menge
 ist die Menge aller Variationen mit Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Variationen mit Wiederholung von n Dingen zur Klasse k (für  ). Sie heißt auch Menge aller Permutationen mit Wiederholung von n Dingen zur Klasse k. Sie hat die oben angegebene Anzahl von Elementen.
). Sie heißt auch Menge aller Permutationen mit Wiederholung von n Dingen zur Klasse k. Sie hat die oben angegebene Anzahl von Elementen.- Beispiel
- Wenn aus 3 Objekten 11 mal mit Zurücklegen gezogen wird, dann sind 311 = 177.147 verschiedene Auswahlen möglich.
- Beispiel Zahlenschloss: Bei einem Zahlenschloss mit 3 Ringen und je 10 Ziffern gibt es 103 = 1000 verschiedene Variationen (000 - 999).
- Beispiel aus Digitaltechnik: Eine Binärzahl kennt 2 Zustände (0 und 1). Mit einer Reihenfolge von x Zahlen können 2x verschiedene Variationen entstehen. Eine vierstellige Binärzahl hat somit 24 = 16 verschiedene Zustände.
Auswählen ohne Beachtung der Reihenfolge (Kombinationen)
Im Gegensatz zu den Variationen werden bei den Kombinationen die Anordnungen außer Acht gelassen, d.h. „abc“ aus „abcde“ ist gleichwertig mit „bca“ aus „abcde“. Es muss also weniger Kombinationen als Variationen geben.
Kombination ohne Zurücklegen
Auswahlprobleme ohne Zurücklegen können als Anordnungsprobleme aufgefasst werden. Die Zahl der möglichen Auswahlen kann ermittelt werden, indem die Zahl der Anordnungen ermittelt wird, bei denen die ausgewählten Objekte auf ausgezeichneten Plätzen angeordnet sind.
Dieses Auswahlproblem kann auf die Ermittlung aller Anordnungen zurückgeführt werden, bei denen die ausgewählten Objekte auf den ersten Plätzen landen, wobei es weder bei den ausgewählten noch bei den nicht ausgewählten Objekten auf die Reihenfolge ankommt.
Wenn aus n Objekten k ohne Zurücklegen und ohne Beachtung der Reihenfolge ausgewählt werden sollen, so gibt es jeweils die Klasse der k ausgewählten Objekte und die Klasse der (n-k) nicht ausgewählten Objekte, in der es auf die Reihenfolge nicht ankommt. Dabei sind k und n-k in der Formel austauschbar, da man die n Objekte in zwei Teilmengen teilt; welche davon die interessierende ist, hat keinen Einfluss auf die Anzahl der möglichen Aufteilungen.
- Demzufolge gibt es
mögliche derartige Auswahlen. Dieser häufig benötigte Ausdruck wird als Binomialkoeffizient bezeichnet.
Mengendarstellung: Die Menge
 ist die Menge aller Kombinationen ohne Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Kombinationen ohne Wiederholung von n Dingen zur Klasse k (für  ). Sie hat die oben angegebene Anzahl von Elementen.
). Sie hat die oben angegebene Anzahl von Elementen.- Beispiel
- Wenn aus 49 Objekten nun 6 ohne Zurücklegen und ohne Beachtung der Reihenfolge ausgewählt werden sollen, wie dies zum Beispiel bei der Ziehung der Lottozahlen der Fall ist, so gibt es
 mögliche Auswahlen.
mögliche Auswahlen.
Kombination mit Zurücklegen (Repetition)
Mengendarstellung: Die Menge
 ist die Menge aller Kombinationen mit Wiederholung von n Dingen zur Klasse k (für
ist die Menge aller Kombinationen mit Wiederholung von n Dingen zur Klasse k (für  ). Sie hat die oben angegebene Anzahl von Elementen.
). Sie hat die oben angegebene Anzahl von Elementen.Hierbei bezeichnet xi die Anzahl des Auftretens des i-ten Elements der Stichprobe.
- Beispiel
- Eine Anwendung davon ist das Gummibärchen-Orakel. Dort wählt man k=5 Bärchen von n=5 Elementen aus (5 Farben). Demnach gibt es
 verschiedene Kombinationen.
verschiedene Kombinationen. - Eine weitere Anwendung ist das Zusammenstellen von 4 (gleichen oder verschiedenen) Farben durch viermaliges Ziehen einer Kugel (k=4) aus einem Topf mit 10 sämtlich unterschiedlich gefärbten Kugeln (n=10), wobei die Kugel nach jeder Ziehung zurückgelegt wird. Somit kann man bei der ersten Ziehung aus 10 Kugeln auswählen, bei der zweiten, dritten und vierten ebenfalls. Wenn man die Reihenfolge der Ziehungen nicht beachtet, so gibt es
 verschiedene Kombinationen.
verschiedene Kombinationen.
Zusammenfassung
Variation (Mit Beachtung der Reihenfolge)

Kombination (Ohne Beachtung der Reihenfolge)
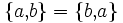
Permutation (Mischen)

mit Wiederholung (Mit Zurücklegen)

Binomialverteilung


ohne Wiederholung (Ohne Zurücklegen)

Hypergeometrische Verteilung

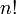
Literatur
- J.H. van Lint, R.M. Wilson: A Course in Combinatorics. Cambridge University Press 1992, ISBN 0-521-42260-4
Weblinks
- Kombinatorik (combinatorial analysis) in Springers Encyclopaedia of Mathematics (englisch)
- Modul Kombinatorik beim MathePrisma
- Links zum Thema Kombinatorik im Open Directory Project
- Surveys in Combinatorics
- Kombinatorik (Vorlesungsskript, PDF)
Wikimedia Foundation.




