- Kompaktheitssatz
-
Der Endlichkeitssatz, auch Kompaktheitssatz genannt, ist einer der wichtigsten Sätze der Aussagenlogik und der Logik erster Stufe. Er besagt: Eine (möglicherweise unendliche) Formelmenge X ist genau dann erfüllbar (d.h. hat ein Modell), wenn jede endliche Teilmenge von X erfüllbar ist. Für die Logik der 2. Stufe gilt dieser Satz nicht.
Eine wichtige Folgerung aus dem Kompaktheitssatz ist, dass jede (möglicherweise unendliche) Formelmenge X, die beliebig große Modelle hat, auch ein unendliches Modell hat. Mit dieser Folgerung ist häufig die Axiomatisierbarkeit von Klassen endlicher L-Strukturen widerlegbar.
Beweis
Für die Prädikatenlogik erster Stufe ergibt sich der Kompaktheitssatz als Korollar aus dem Gödel'schen Vollständigkeitssatz sowie als Folgerung aus dem Satz von Herbrand. Dementsprechend kurz gestaltet sich auch der Beweis:
„
 “: Angenommen, X hat ein Modell. Dann ist dieses (trivialerweise) auch ein Modell einer jeden endlichen Teilmenge von X.
“: Angenommen, X hat ein Modell. Dann ist dieses (trivialerweise) auch ein Modell einer jeden endlichen Teilmenge von X.„
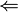 “: Angenommen, jede endliche Menge
“: Angenommen, jede endliche Menge 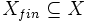 besitzt ein Modell. Zur Erzeugung eines Widerspruchs wird angenommen, X habe kein Modell. Dann ist aus X in einem vollständigen und korrekten formalen System ein Widerspruch (z.B.
besitzt ein Modell. Zur Erzeugung eines Widerspruchs wird angenommen, X habe kein Modell. Dann ist aus X in einem vollständigen und korrekten formalen System ein Widerspruch (z.B. 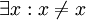 ) herleitbar (Vollständigkeitssatz). Da eine Herleitung in einem formalen System (nach Definition) endlich ist, können in dieser Herleitung auch nur endlich viele Formeln aus X verwendet worden sein. Also ist aus einer endlichen Teilmenge von X ein Widerspruch herleitbar, und diese besitzt somit kein Modell (Korrektheitssatz). Widerspruch. Also besitzt X doch ein Modell.
) herleitbar (Vollständigkeitssatz). Da eine Herleitung in einem formalen System (nach Definition) endlich ist, können in dieser Herleitung auch nur endlich viele Formeln aus X verwendet worden sein. Also ist aus einer endlichen Teilmenge von X ein Widerspruch herleitbar, und diese besitzt somit kein Modell (Korrektheitssatz). Widerspruch. Also besitzt X doch ein Modell.Im Kern des Beweises steht das folgende Ergebnis, das direkt aus dem Gödel'schen Vollständigkeitssatz folgt:
Folgt eine Formel φ aus einer Formelmenge X, so gibt es eine endliche Menge
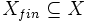 , sodass φ aus Xfin folgt.
, sodass φ aus Xfin folgt.(
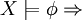 es gibt endliches
es gibt endliches 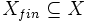 mit
mit 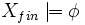 )
)Weblinks
Wikimedia Foundation.
