Komplement (Mengen)

In der Mengentheorie und anderen Teilgebieten der Mathematik sind zwei verschiedene Komplemente definiert: Das relative Komplement und das absolute Komplement.

Relatives Komplement

Sind A und B Mengen, dann ist das relative Komplement (auch mengentheoretisches Komplement) von A in B die Menge aller Elemente aus B, welche nicht in A sind. Das relative Komplement von A in B wird als B \ A notiert (manchmal auch als B - A, doch diese Notation ist mehrdeutig, da es in bestimmten Zusammenhängen als die Menge aller b-a interpretiert werden kann, wobei b Elemente aus B und a Elemente aus A sind).

Formal: $B \setminus A = \{x \in B ~|~ x \not \in A\}$ .

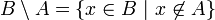Beispiele:

• {1,2,3} \ {2,3,4} = {1}
• {2,3,4} \ {1,2,3} = {4}
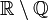• Ist $\mathbb R$ die Menge aller reellen Zahlen und $\mathbb Q$ die Menge aller rationalen Zahlen, so ist $\mathbb R \setminus \mathbb Q$ die Menge der irrationalen Zahlen.

Im Folgenden sind einige Eigenschaften relativer Komplemente im Zusammenhang mit den mengentheoretischen Operationen Vereinigung und Durchschnitt aufgelistet:

Seien A, B und C Mengen. Dann gelten folgende Identitäten:

• C \ (A ∩ B) = (C \ A) ∪ (C \ B)
• C \ (A ∪ B) = (C \ A) ∩ (C \ B)
• C \ (B \ A) = (A ∩ C) ∪ (C \ B)
• (B \ A) ∩ C = (B ∩ C) \ A = B ∩ (C \ A)
• (B \ A) ∪ C = (B ∪ C) \ (A \ C)
• A \ A = Ø
• Ø \ A = Ø
• A \ Ø = A

Absolutes Komplement

Das Komplement von A in U

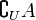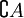Ist ein Universum U definiert, so wird das relative Komplement von A in U auch absolutes Komplement (oder einfach Komplement) von A genannt und als A^C (manchmal auch als A′, oder auch als $\complement_U A$ bzw. $\complement A$ wenn U fest ist) notiert, es ist also: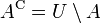

$A^{\rm C} = U \setminus A$

Ist das Universum zum Beispiel die Menge der natürlichen Zahlen, so ist das (absolute) Komplement der Menge der geraden Zahlen die Menge der ungeraden Zahlen.

Im Folgenden sind einige Eigenschaften absoluter Komplemente im Zusammenhang mit den mengentheoretischen Operationen Vereinigung und Durchschnitt aufgelistet:

Seien A und B Mengen im Universum U, dann gelten folgende Identitäten:

De Morgansche Regeln:

• (A ∪ B)^C = A^C ∩ B^C
• (A ∩ B)^C = A^C ∪ B^C

Komplementgesetze:

• A ∪ A^C = U
• A ∩ A^C = Ø
• Ø^C = U
• U^C = Ø
• Ist A ⊆ B, so ist B^C ⊆ A^C

Involution:

• A^CC = A

Beziehungen zwischen relativen und absoluten Komplementen:

• A \ B = A ∩ B^C
• (A \ B)^C = A^C ∪ B

Die ersten beiden Komplementgesetze zeigen, dass, wenn A eine nichtleere Teilmenge von U ist, {A, A^C} eine Partition von U ist.