- Komplement (Mengenlehre)
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
∁In der Mengentheorie und anderen Teilgebieten der Mathematik sind zwei verschiedene Komplemente definiert: Das relative Komplement und das absolute Komplement.
Inhaltsverzeichnis
Relatives Komplement
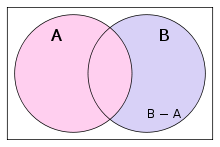
Sind A und B Mengen und A sei eine Teilmenge von B, dann ist das relative Komplement, auch mengentheoretisches Komplement oder mengentheoretische Differenz genannt, genau jene Menge B ohne die Elemente aus A. Man schreibt auch
 oder im Sinne der Differenz B − A und sagt „B ohne A“ – die englische Leseart „B take away A“ beschreibt sehr gut, was passiert.
oder im Sinne der Differenz B − A und sagt „B ohne A“ – die englische Leseart „B take away A“ beschreibt sehr gut, was passiert.Das Komplement unterscheidet sich von der normalen Subtraktion von Mengen nur dadurch, dass die Teilmengenbeziehung zwischen den betrachteten Mengen bestehen muss.
Relativ heißt es deshalb, weil man für eine Menge A das Komplement nicht angeben kann, ohne den Kontext zu kennen. Ist eine Menge B hingegen fixiert, so kann man
 anstelle von „das relative Komplement von A in B“ auch einfach nur das Komplement von A nennen.
anstelle von „das relative Komplement von A in B“ auch einfach nur das Komplement von A nennen.- formale Definition
- Beispiele
-


- Für
 (reelle Zahlen) und
(reelle Zahlen) und  (rationale Zahlen), ist
(rationale Zahlen), ist  die Menge der irrationalen Zahlen.
die Menge der irrationalen Zahlen.
Eigenschaften
Im Folgenden sind einige Eigenschaften relativer Komplemente im Zusammenhang mit den mengentheoretischen Operationen Vereinigung und Durchschnitt aufgelistet:
Seien A, B und C Mengen. Dann gelten folgende Identitäten:
Absolutes Komplement
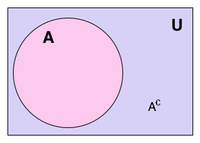
Ist ein Universum U definiert, so wird für jede Menge A ⊆ U das relative Komplement von A in U auch absolutes Komplement (oder einfach Komplement) von A genannt und als AC (manchmal auch als A′, oder auch als A,
 bzw.
bzw.  wenn U fest ist) notiert, es ist also:
wenn U fest ist) notiert, es ist also:
Ist das Universum zum Beispiel die Menge der natürlichen Zahlen, so ist das (absolute) Komplement der Menge der geraden Zahlen die Menge der ungeraden Zahlen.
Im Folgenden sind einige Eigenschaften absoluter Komplemente im Zusammenhang mit den mengentheoretischen Operationen Vereinigung und Durchschnitt aufgelistet:
Seien A und B Teilmengen des Universums U, dann gelten folgende Identitäten:
- De Morgansche Regeln:
-
- Komplementgesetze:
-
- A ∪ AC = U
- A ∩ AC = Ø
- ØC = U
- UC = Ø
- Ist A ⊆ B, so ist BC ⊆ AC
-
- Involution:
-
- ACC = A
-
- Beziehungen zwischen relativen und absoluten Komplementen:
-
- A \ B = A ∩ BC
- (A \ B)C = AC ∪ B
-
Die ersten beiden Komplementgesetze zeigen, dass, wenn A eine nichtleere Teilmenge von U ist, {A, AC} eine Partition von U ist.
Siehe auch
Literatur
- Oliver Deiser: Einführung in die Mengenlehre, Springer, 2004, ISBN 978-3540204015
Wikimedia Foundation.