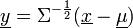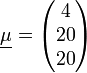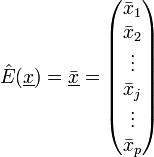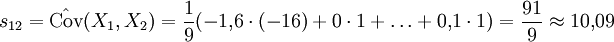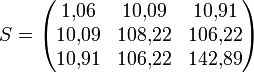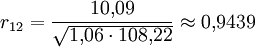Korrelationsmatrix

Die gemeinsame Wahrscheinlichkeitsverteilung mehrerer Zufallsvariablen nennt man multivariate Verteilung oder auch mehrdimensionale Verteilung.

Formale Darstellung

Um Verwechslungen zu vermeiden, werden im Folgenden skalare Zufallsvariablen groß geschrieben, Zufallsvektoren dagegen klein. Ferner werden jegliche Vektoren unterstrichen.

Man betrachtet p Zufallsvariablen $X_j\ (j=1, \ldots, p)$, jeweils mit einem Erwartungswert E(X_j) und der Varianz V(X_j). Die Zufallsvariablen sind zudem paarweise korreliert mit der Kovarianz $\operatorname{Cov}(X_j,X_k)\ (j,k=1,\ldots,p; j\ne k)$.

Die Verteilung ist nun die gemeinsame Wahrscheinlichkeit, dass alle X_j höchstens gleich einer jeweiligen Konstanten x_j sind, also

$P(X_1 \le x_1,X_2 \le x_2,\ldots, X_p \le x_p) = F_X(x_1,x_2,\ldots, x_p)$.

Multivariate Zufallsvariablen werden i.A. in einem Zufallsvektor 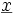$\underline x$ zusammengefasst:

$\underline x = \begin{pmatrix} X_1 \\ X_2 \\ \vdots\\ X_p \end{pmatrix}$ .

Die Verteilung ist somit

$F_x(\underline x)=F_X(x_1, x_2, \ldots, x_p)$.

Die Erwartungswerte befinden sich im Erwartungswertvektor

$E(\underline x)= \begin{pmatrix} E(X_1) \\ E(X_2) \\ \vdots\\ E(X_p) \end{pmatrix}$

der meist mit 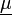$\underline \mu$ bezeichnet wird.

Die Varianzen werden zusammen mit den Kovarianzen in der (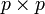$p\times p$)-Kovarianzmatrix Σ aufgeführt:

$\Sigma= \begin{pmatrix} V(X_1) & {\rm Cov}(X_1,X_2) & {\rm Cov}(X_1,X_3) & \ldots & {\rm Cov}(X_1,X_p) \\ {\rm Cov}(X_2,X_1) & V(X_2) & {\rm Cov}(X_2,X_3) & \ldots & {\rm Cov}(X_2,X_p) \\ {\rm Cov}(X_3,X_1) & {\rm Cov}(X_3,X_2) & V(X_3) & \ldots & {\rm Cov}(X_3,X_p) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {\rm Cov}(X_p,X_1) & {\rm Cov}(X_p,X_2) & {\rm Cov}(X_p,X_3) & \ldots & V(X_p) \\ \end{pmatrix}$

Σ ist symmetrisch mit den Varianzen auf der Hauptdiagonalen. 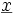$\underline x$ ist also verteilt mit dem Erwartungswertvektor $E(\underline x)$ und der Kovarianzmatrix Σ.

Die Umformung zu den Korrelationskoeffizienten

$\rho_{jk}={{\rm Cov}(X_j,X_k) \over\ \sqrt{V(X_j) \cdot V(X_k)}}$

ergibt im Falle positiver Varianzen die Korrelationsmatrix

$R = \begin{pmatrix} 1 & \rho_{12} & \rho_{13} & \ldots & \rho_{1p} \\ \rho_{21} & 1 & \rho_{23} & \ldots & \rho_{2p} \\ \rho_{31} & \rho_{32} & 1 & \ldots & \rho_{3p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \rho_{p1} & \rho_{p2} & \rho_{p3} & \ldots & 1\\ \end{pmatrix}$

Gemeinsame Wahrscheinlichkeiten sind häufig schwierig zu berechnen, vor allem, wenn schon die Einzelwahrscheinlichkeiten nicht analytisch bestimmbar sind. Man behilft sich dann gegebenenfalls mit Abschätzungen. Vor allem können die Auswirkungen der Kovarianz auf die Verteilung in der Regel nicht abgesehen werden.

Sind die Zufallsvariablen stochastisch unabhängig, ist die gemeinsame Verteilung gleich dem Produkt der entsprechenden Einzelverteilungen, den Rand- oder auch Marginalverteilungen.

$F_x(\underline x) = F_X(x_1, x_2, \ldots, x_p) = F_{X_1}(x_1) F_{X_2}(x_2) \cdots F_{X_p}(x_p)$.

Ausgewählte multivariate Verteilungen

Von Bedeutung sind vor allem die

• multivariate Normalverteilung,
• Hotelling t-Verteilung als multivariate t-Verteilung,
• Wishart-Verteilung als multivariate Chi-Quadrat-Verteilung,

die multivariaten Verfahren zu Grunde liegen. Meistens ist es möglich, mittels einer linearen Transformation den Zufallsvektor in ein Skalar umzuwandeln, das dann univariat verteilt ist und so als Testprüfgröße fungiert.

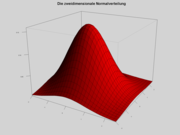
Die multivariate Normalverteilung

Dichte der zweidimensionalen Standardnormalverteilung

Gegeben ist ein Vektor 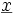$\underline x$ aus p gemeinsam normalverteilten Zufallsvariablen mit dem Erwartungswertvektor μ und der Kovarianzmatrix Σ mit Determinante | Σ | , d. h. die gemeinsame Dichtefunktion der Vektorkomponenten sei gegeben durch

$f_x(\underline x)=\frac 1{(2\pi)^{\frac p2}|\Sigma|^{\frac 12}} \exp\left(-{\frac 12}(\underline x-\underline \mu)^T\Sigma^{-1}(\underline x-\underline \mu)\right)$.

Wir schreiben:

$\underline x\sim \mathcal N_p(\underline \mu, \Sigma)$.

Die Kovarianzmatrix Σ ist positiv semidefinit. Die Werte der Verteilungsfunktion F müssen numerisch ermittelt werden.

Die multivariate Normalverteilung hat spezielle Eigenschaften:

• Sind die Komponenten des Zufallsvektors 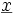$\underline x$ paarweise unkorreliert, sind sie auch stochastisch unabhängig.

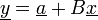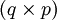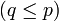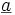• Die lineare Transformation $\underline y = \underline a + B\underline x$ mit B als $(q\times p)$-Matrix $(q \le p)$ und $\underline a$ als Vektor der Länge q ist q-dimensional normalverteilt als $\mathcal N_q(\underline a + B\underline \mu, B\Sigma B^T)$.

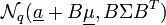• Die lineare Transformation

$\underline y = \Sigma^{-\frac 12}(\underline x-\underline \mu)$

standardisiert den Zufallsvektor x. Es ist

$\underline Y \sim N_p(\underline 0,\underline 1)$.

also sind die Komponenten von y stochastisch unabhängig.

• X kann auch eine singuläre Kovarianzmatrix besitzen. Man spricht dann von einer degenerierten oder singulären multivariaten Normalverteilung.

Beispiel für eine multivariate Normalverteilung

Betrachtet wird eine Apfelbaumplantage mit sehr vielen gleich alten, also vergleichbaren Apfelbäumen. Man interessiert sich für die Merkmale Größe der Apfelbäume, die Zahl der Blätter und die Erträge. Es werden also die Zufallsvariablen definiert:

X₁: Höhe eines Baumes [m]; X₂: Ertrag [100 kg]; X₃: Zahl der Blätter [1000 Stück].

Die Variablen sind jeweils normalverteilt wie

X₁˜N(4;1);X₂˜N(20;100);X₃˜N(20;225);

Die meisten Bäume sind also um 4 ± 1m groß, sehr kleine oder sehr große Bäume sind eher selten. Bei einem großen Baum ist der Ertrag tendenziell größer als bei einem kleinen Baum, aber es gibt natürlich hin und wieder einen großen Baum mit wenig Ertrag. Ertrag und Größe sind korreliert, die Kovarianz beträgt Cov(X₁,X₂) = 9 und der Korrelationskoeffizient ρ₁₂ = 0,9.

Ebenso ist 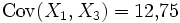$\operatorname{Cov}(X_1,X_3)=12{,}75$ mit dem Korrelationskoeffizienten ρ₁₃ = 0,85, und 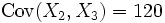$\operatorname{Cov}(X_2,X_3)=120$ mit dem Korrelationskoeffzienten ρ₂₃ = 0,8.

Fasst man die drei Zufallsvariablen im Zufallsvektor 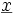$\underline x$ zusammen, ist 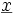$\underline x$ multivariat normalverteilt mit

$\underline \mu = \begin{pmatrix} 4\\ 20\\ 20 \end{pmatrix}$

und

$\Sigma= \begin{pmatrix} 1 & 9 & 12{,}75\\ 9 & 100 & 120\\ 12{,}75 & 120 & 225 \end{pmatrix}$ .

Die entsprechende Korrelationsmatrix ist

$R= \begin{pmatrix} 1 & 0{,}9 & 0{,}85\\ 0{,}9 & 1 & 0{,}8\\ 0{,}85 & 0{,}8 & 1 \end{pmatrix}$.

Stichproben bei multivariaten Verteilungen

In der Realität werden in aller Regel die Verteilungsparameter einer multivariaten Verteilung nicht bekannt sein. Diese Parameter müssen also geschätzt werden.

Man zieht eine Stichprobe vom Umfang n. Jede Realisation 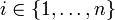$i\in\{1,\ldots,n\}$ des Zufallsvektors 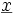$\underline x$ könnte man als Punkt in einem p-dimensionalen Hyperraum auffassen. Man erhält so die 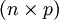$(n\times p)$-Datenmatrix X als

$X= \begin{pmatrix} x_{11}& x_{12}& \cdots &x_{1j}&\cdots &x_{1p}\\ x_{21}& x_{22}& \cdots &x_{2j}&\cdots &x_{2p}\\ \vdots& & & & &\vdots \\ x_{i1}& x_{i2}& \cdots &x_{ij}&\cdots &x_{ip}\\ \vdots& & & & &\vdots \\ x_{n1}& x_{n2}& \cdots &x_{nj}&\cdots &x_{np} \end{pmatrix}$,

die in jeder Zeile die Koordinaten eines Punktes enthält.

Der Erwartungswertvektor wird geschätzt durch den Mittelwertvektor der p arithmetischen Mittelwerte

$\hat E(\underline x)=\underline{\bar x}= \begin{pmatrix} \bar x_1\\ \bar x_2\\ \vdots\\ \bar x_j\\ \vdots\\ \bar x_p \end{pmatrix}$

mit den Komponenten

$\bar x_j = \frac 1n\sum_{i=1}^n x_{ij}$.

Für die Schätzung der Kovarianzmatrix erweist sich die bezüglich der arithmetischen Mittelwerte zentrierte Datenmatrix X ^* als nützlich. Sie berechnet sich als

$X^*=X-\underline 1\cdot\underline{\bar x}^T$,

mit den Elementen 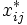$x^*_{ij}$, wobei 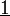$\underline 1$ einen Spaltenvektor der Länge n mit lauter Einsen darstellt.

Die 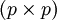$(p\times p)$-Kovarianzmatrix hat die geschätzten Komponenten

$s_{jk}=\hat\operatorname{Cov}(X_j,X_k)=\frac 1{n-1}\sum_{i=1}^n x^*_{ij}x^*_{ik}$.

Sie ergibt sich als

$\widehat\Sigma = S = \frac 1{n-1}X^{*T}X^*$.

Die Korrelationsmatrix R wird geschätzt durch die paarweisen Korrelationskoeffizienten

$r_{jk} = \frac{\sum\limits_{i=1}^n x^*_{ij}x^*_{ik}} {\sqrt{\sum\limits_{i=1}^n {x^*_{ij}}^2}\sqrt{\sum\limits_{i=1}^n {x^*_{ik}}^2}}$,

auf ihrer Hauptdiagonalen stehen Einsen.

Beispiel zu Stichproben

Es wurden 10 Apfelbäume zufällig ausgewählt. Die 10 Beobachtungen werden in der Datenmatrix X zusammengefasst:

$X= \begin{pmatrix} 3{,}3&24& 27 \\ 4{,}9& 41&55\\ 5{,}9& 46&52 \\ 5{,}2& 49&54\\ 3{,}6& 29 &34 \\ 4{,}2&33& 51 \\ 5{,}0&42& 43\\ 5{,}1&35& 54 \\ 6{,}8&60& 70 \\ 5{,}0&41&50 \end{pmatrix}$ .

Die Mittelwerte berechnen sich, wie beispielhaft an 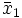$\bar x_1$ gezeigt, als

$\bar x_1=\frac{1}{10}(3{,}3+4{,}9+\ldots+5{,}0)=4{,}9$.

Sie ergeben den Mittelwertvektor

$\underline{\bar x}= \begin{pmatrix} 4{,}9\\ 40\\ 49 \end{pmatrix}$

Für die zentrierte Datenmatrix X ^* erhält man die zentrierten Beobachtungen, indem man von den Spalten den entsprechenden Mittelwert abzieht:

3,3 - 4,9 = -1,6;	24 – 40 = -16;	27 - 49 = -22
4,9 - 4,9 = 0;	41 - 40 = 1;	55 - 49 = 6
	...

,

also

$X^*= \begin{pmatrix} -1{,}6&-16& -22 \\ 0{,}0& 1&6\\ 1{,}0& 6&3 \\ 0{,}3& 9&5\\ -1{,}3& -11 &-15 \\ -0{,}7&-7& 2 \\ 0{,}1&2& -6\\ 0{,}2&-5& 5 \\ 1{,}9&20& 21 \\ 0{,}1&1&1 \end{pmatrix}$.

Man berechnet für die Kovarianzmatrix die Kovarianzen, wie im Beispiel,

$s_{12}=\hat\operatorname{Cov}(X_1,X_2)=\frac 19(-1{,}6 \cdot (-16)+0\cdot 1+\ldots+0{,}1\cdot 1) =\frac{91}{9}\approx 10{,}09$

und entsprechend die Varianzen

$s_{22}=\hat V(X_2)=\frac 19((-16)^2 +1^2+...+1^2) =\frac{974}{9}\approx 108{,}22$ ,

so dass sich die Kovarianzmatrix

$S= \begin{pmatrix} 1{,}06&10{,}09&10{,}91 \\ 10{,}09& 108{,}22&106{,}22\\ 10{,}91& 106{,}22&142{,}89 \end{pmatrix}$

ergibt.

Entsprechend erhält man für die Korrelationsmatrix zum Beispiel

$r_{12}=\frac{10{,}09}{\sqrt{1{,}06\cdot 108{,}22 }} \approx 0{,}9439$

bzw. insgesamt

$R= \begin{pmatrix} 1&0{,}9439&0{,}8884 \\ 0{,}9439& 1&0{,}8542\\ 0{,}8884& 0{,}8542&1 \end{pmatrix}$.

Literatur

• Mardia, KV, Kent, JT, Bibby, JM: Multivariate Analysis, New York 1979
• Fahrmeir, Ludwig, Hamerle, Alfred, Tutz, Gerhard (Hrsg): Multivariate statistische Verfahren, New York 1996
• Hartung, Joachim, Elpelt, Bärbel: Multivariate Statistik, München, Wien 1999

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart