- Mehrdimensionale Normalverteilung
-
Die mehrdimensionale oder multivariate Normalverteilung ist ein Typ multivariater Wahrscheinlichkeitsverteilungen und stellt eine Verallgemeinerung der (eindimensionalen) Normalverteilung auf mehrere Dimensionen dar.[1]
Bestimmt wird eine multivariate Normalverteilung durch zwei Verteilungsparameter - den Vektor der Erwartungswerte der eindimensionalen Komponenten μ und durch die Kovarianzmatrix Σ, welche den Parametern μ und σ2 der eindimensionalen Normalverteilungen entsprechen.
Multivariat normalverteilte Zufallsvariablen treten als Grenzwerte bestimmter Summen unabhängiger mehrdimensionaler Zufallsvariabler auf. Dies ist die Übertragung des zentralen Grenzwertsatz auf den mehrdimensionalen Fall.
Weil sie entsprechend dort auftreten, wo mehrdimensionale zufällige Größen als Überlagerung vieler voneinander unabhängiger Einzeleffekte angesehen werden können, haben sie für die Praxis eine große Bedeutung.
Aufgrund der sogenannten Reproduktionseigenschaft der multivariaten Normalverteilung lässt sich die Verteilung von Summen (und Linearkombinationen) multivariat normalverteiler Zufallsvariablen konkret angeben, was auf dem Gebiet der multivariaten Statistik eine Rolle spielt.
Die multivariate Normalverteilung: allgemeiner Fall
Eine p-dimensionale reelle Zufallvariable X ist normalverteilt mit Erwartungswertvektor μ und (positiv definiter) Kovarianzmatrix Σ, wenn sie eine Dichtefunktion der Form
besitzt. Hier bezeichnet | Σ | die Determinante der Kovarianzmatrix.
Man schreibt
Für die zugehörige Verteilungsfunktion F gibt es keine geschlossene Formel. Die entsprechenden Integrale müssen numerisch berechnet werden.
Die multivariate Normalverteilung hat die folgenden Eigenschaften:
- Sind die Komponenten von X paarweise unkorreliert, so sind sie auch stochastisch unabhängig.
- Die lineare Transformation
 mit einer Matrix
mit einer Matrix  (mit
(mit  ) und
) und  ist q-dimensional normalverteilt:
ist q-dimensional normalverteilt:  . Dies gilt aber nach der hier gegebenen Definition nur, wenn
. Dies gilt aber nach der hier gegebenen Definition nur, wenn  nicht-singulär ist, also eine nicht-verschwindende Determinante hat.
nicht-singulär ist, also eine nicht-verschwindende Determinante hat.
- Die lineare Transformation
-
- standardisiert den Zufallsvektor
 : es ist
: es ist  (mit Einheitsmatrix E).
(mit Einheitsmatrix E).
 kann auch eine singuläre Kovarianzmatrix besitzen. Man spricht dann von einer degenerierten oder singulären multivariaten Normalverteilung. In diesem Fall existiert keine Dichtefunktion.
kann auch eine singuläre Kovarianzmatrix besitzen. Man spricht dann von einer degenerierten oder singulären multivariaten Normalverteilung. In diesem Fall existiert keine Dichtefunktion.
- Bedingte Verteilung bei partieller Kenntnis des Zufallsvektors: Bedingt man einen multivariat normal verteilten Zufallsvektor auf einen Teilvektor, so ist das Ergebnis selbst wieder multivariat normal verteilt, für
-
- gilt
 ,
,
- insbesondere hängt der Erwartungswert linear vom Wert von X2 ab und die Varianz ist unabhängig vom Wert von X2.
Die p-dimensionale Standardnormalverteilung
Das Wahrscheinlichkeitsmaß auf
 , das durch die Dichtefunktion
, das durch die Dichtefunktiondefiniert wird, heißt Standardnormalverteilung der Dimension p. Die p-dimensionale Standardnormalverteilung ist abgesehen von Translationen (d. h. Erwartungswert
 ) die einzige multivariate Verteilung, deren Komponenten stochastisch unabhängig sind und deren Dichte zugleich rotationssymmetrisch ist.
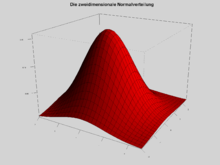
) die einzige multivariate Verteilung, deren Komponenten stochastisch unabhängig sind und deren Dichte zugleich rotationssymmetrisch ist.Dichte der zweidimensionalen Normalverteilung
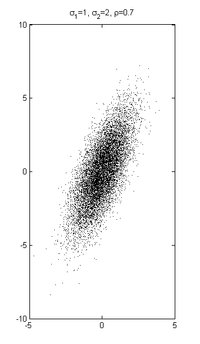
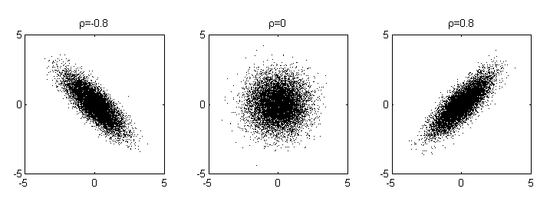
Die Dichtefunktion der zweidimensionalen Normalverteilung mit Mittelwert = (0,0),
 und Korrelationskoeffizient
und Korrelationskoeffizient  ist
istIm allgemeineren zweidimensionalen Fall mit Mittelwert = (0,0) und beliebigen Varianzen ist die Dichtefunktion
und den allgemeinsten Fall mit Mittelwert = (μ1,μ2) bekommt man durch Translation (ersetze x1 durch x1 − μ1 und x2 durch x2 − μ2).
Beispiel für eine multivariate Normalverteilung
Betrachtet wird eine Apfelbaumplantage mit sehr vielen gleich alten, also vergleichbaren Apfelbäumen. Man interessiert sich für die Merkmale Größe der Apfelbäume, die Zahl der Blätter und die Erträge. Es werden also die Zufallsvariablen definiert:
X1: Höhe eines Baumes [m]; X2: Ertrag [100 kg]; X3: Zahl der Blätter [1000 Stück].
Die Variablen sind jeweils normalverteilt wie
- X1∼N(4;1);X2∼N(20;100);X3∼N(20;225);.
Die meisten Bäume sind also um 4 ± 1m groß, sehr kleine oder sehr große Bäume sind eher selten. Bei einem großen Baum ist der Ertrag tendenziell größer als bei einem kleinen Baum, aber es gibt natürlich hin und wieder einen großen Baum mit wenig Ertrag. Ertrag und Größe sind korreliert, die Kovarianz beträgt Cov(X1,X2) = 9 und der Korrelationskoeffizient
 .
.Ebenso ist
 mit dem Korrelationskoeffizienten
mit dem Korrelationskoeffizienten  , und
, und  mit dem Korrelationskoeffzienten
mit dem Korrelationskoeffzienten  .
.Fasst man die drei Zufallsvariablen im Zufallsvektor
 zusammen, ist
zusammen, ist  multivariat normalverteilt mit
multivariat normalverteilt mitund
Die entsprechende Korrelationsmatrix ist
Stichproben bei multivariaten Verteilungen
In der Realität werden in aller Regel die Verteilungsparameter einer multivariaten Verteilung nicht bekannt sein. Diese Parameter müssen also geschätzt werden.
Man zieht eine Stichprobe vom Umfang n. Jede Realisation
 des Zufallsvektors
des Zufallsvektors  könnte man als Punkt in einem p-dimensionalen Hyperraum auffassen. Man erhält so die
könnte man als Punkt in einem p-dimensionalen Hyperraum auffassen. Man erhält so die  -Datenmatrix X als
-Datenmatrix X alsdie in jeder Zeile die Koordinaten eines Punktes enthält.
Der Erwartungswertvektor wird geschätzt durch den Mittelwertvektor der p arithmetischen Mittelwerte
mit den Komponenten
Für die Schätzung der Kovarianzmatrix erweist sich die bezüglich der arithmetischen Mittelwerte zentrierte Datenmatrix X * als nützlich. Sie berechnet sich als
mit den Elementen
 , wobei
, wobei  einen Spaltenvektor der Länge n mit lauter Einsen darstellt.
einen Spaltenvektor der Länge n mit lauter Einsen darstellt.Die
 -Kovarianzmatrix hat die geschätzten Komponenten
-Kovarianzmatrix hat die geschätzten KomponentenSie ergibt sich als
Die Korrelationsmatrix R wird geschätzt durch die paarweisen Korrelationskoeffizienten
auf ihrer Hauptdiagonalen stehen Einsen.
Beispiel zu Stichproben
Es wurden 10 Apfelbäume zufällig ausgewählt und jeweils 3 Eigenschaften gemessen: X1: Höhe eines Baumes [m]; X2: Ertrag [100 kg]; X3: Zahl der Blätter [1000 Stück]. Diese 10 Beobachtungen werden in der Datenmatrix X zusammengefasst:
Die Mittelwerte berechnen sich, wie beispielhaft an
 gezeigt, als
gezeigt, alsSie ergeben den Mittelwertvektor
Für die zentrierte Datenmatrix X * erhält man die zentrierten Beobachtungen, indem von den Spalten der entsprechende Mittelwert abzogen wird:
also
Man berechnet für die Kovarianzmatrix die Kovarianzen, wie im Beispiel,
und entsprechend die Varianzen
so dass sich die Kovarianzmatrix
ergibt.
Entsprechend erhält man für die Korrelationsmatrix zum Beispiel
bzw. insgesamt
Erzeugung mehrdimensionaler, normalverteilter Zufallszahlen
Eine oft verwendete Methode zur Erzeugung eines Zufallsvektors X einer N-dimensionalen Normalverteilung mit Mittelwertvektor μ und (symmetrischer und positiv definiter) Kovarianzmatrix Σ kann wie folgt angegeben werden:
- Bestimme eine Matrix A, so dass AAT = Σ. Dies ist oft die Cholesky-Zerlegung von Σ, allerdings genügt auch in den meisten Fällen die Wurzel von Σ.
- Sei
 ein Vektor, dessen Komponenten N stochastisch unabhängige, standardnormalverteilte Zufallszahlen sind. Diese können beispielsweise mit Hilfe der Box-Muller-Methode generiert werden.
ein Vektor, dessen Komponenten N stochastisch unabhängige, standardnormalverteilte Zufallszahlen sind. Diese können beispielsweise mit Hilfe der Box-Muller-Methode generiert werden. - Mit X = μ + AZ ergibt sich aufgrund der affinen Abbildung die gewünschte Verteilung.
Anmerkungen
- ↑ Mehrdimensionale und multivariate Normalverteilung werden in diesem Artikel synonym verwendet. Bei Hartung/Elpelt: Multivariate Statistik haben sie aber (in Kapitel 1, Abschnitt 5) unterschiedliche Bedeutungen: hier ist die multivariate Normalverteilung eine Matrix-Verteilung.
Literatur
- Mardia, KV, Kent, JT, Bibby, JM: Multivariate Analysis, New York 1979
- Fahrmeir, Ludwig, Hamerle, Alfred, Tutz, Gerhard (Hrsg): Multivariate statistische Verfahren, New York 1996
- Hartung, Joachim, Elpelt, Bärbel: Multivariate Statistik, München, Wien 1999
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
mehrdimensionale Normalverteilung — normalusis daugiamatis skirstinys statusas T sritis fizika atitikmenys: angl. multivariate normal distribution vok. mehrdimensionale Normalverteilung, f rus. многомерное нормальное распределение, n pranc. distribution normale multivariée, f … Fizikos terminų žodynas
Normalverteilung — Dichtefunktionen der Normalverteilungen (blau), (grün) und (rot) Die Normal oder Gauß Verteilung … Deutsch Wikipedia
Normalverteilung — Gaußverteilung * * * Nor|mal|ver|tei|lung: svw. ↑ Gauß Verteilung. * * * I Normalverteilung, Verteilung. II Normalverteilung, Statistik. III Norma … Universal-Lexikon
Multivariate Normalverteilung — Die gemeinsame Wahrscheinlichkeitsverteilung mehrerer Zufallsvariablen nennt man multivariate Verteilung oder auch mehrdimensionale Verteilung. Inhaltsverzeichnis 1 Formale Darstellung 2 Ausgewählte multivariate Verteilungen 3 Die multivariate… … Deutsch Wikipedia
Canny-Detektor — Der Canny Algorithmus, benannt nach John Canny, ist ein in der digitalen Bildverarbeitung weit verbreiteter, robuster Algorithmus zur Kantendetektion. Er gliedert sich in verschiedene Faltungsoperationen und liefert ein Bild, welches idealerweise … Deutsch Wikipedia
Canny-Kantendetektor — Der Canny Algorithmus, benannt nach John Canny, ist ein in der digitalen Bildverarbeitung weit verbreiteter, robuster Algorithmus zur Kantendetektion. Er gliedert sich in verschiedene Faltungsoperationen und liefert ein Bild, welches idealerweise … Deutsch Wikipedia
Multivariate Verteilung — Die Wahrscheinlichkeitsverteilung einer mehrdimensionalen Zufallsvariable nennt man multivariate Verteilung oder auch mehrdimensionale Verteilung. Inhaltsverzeichnis 1 Einführendes Beispiel 2 Zweidimensionale Verteilungsfunktion 3 Der allgemeine… … Deutsch Wikipedia
Canny-Algorithmus — Der Canny Algorithmus, benannt nach John Canny[1], ist ein in der digitalen Bildverarbeitung weit verbreiteter, robuster Algorithmus zur Kantendetektion. Er gliedert sich in verschiedene Faltungsoperationen und liefert ein Bild, welches… … Deutsch Wikipedia
Gauss-Prozess — Ein stochastischer Prozess auf einer beliebigen Indexmenge T wird Gauß Prozess (nach Carl Friedrich Gauß) genannt, wenn seine endlichdimensionalen Verteilungen (mehrdimensionale) Normalverteilungen (auch Gauß Verteilungen, daher der Name) sind.… … Deutsch Wikipedia
distribution normale multivariée — normalusis daugiamatis skirstinys statusas T sritis fizika atitikmenys: angl. multivariate normal distribution vok. mehrdimensionale Normalverteilung, f rus. многомерное нормальное распределение, n pranc. distribution normale multivariée, f … Fizikos terminų žodynas







![f_X(x_1,x_2)
=
\frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1-\varrho^2}} \,
\exp
\left(
-\frac{1}{2 (1-\varrho^2)}
\left[
\frac{x_1^2}{\sigma_1^2} +
\frac{x_2^2}{\sigma_2^2} -
\frac{2 \varrho x_1 x_2}{\sigma_1 \sigma_2}
\right]
\right),](6/a163d2fc533d26ae4b060f1377e24dd5.png)



















