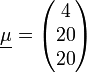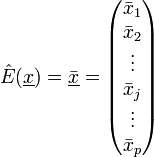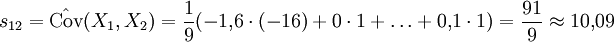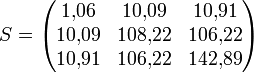- Multivariate Normalverteilung
-
Die gemeinsame Wahrscheinlichkeitsverteilung mehrerer Zufallsvariablen nennt man multivariate Verteilung oder auch mehrdimensionale Verteilung.
Inhaltsverzeichnis
Formale Darstellung
Um Verwechslungen zu vermeiden, werden im Folgenden skalare Zufallsvariablen groß geschrieben, Zufallsvektoren dagegen klein. Ferner werden jegliche Vektoren unterstrichen.
Man betrachtet p Zufallsvariablen
 , jeweils mit einem Erwartungswert E(Xj) und der Varianz V(Xj). Die Zufallsvariablen sind zudem paarweise korreliert mit der Kovarianz
, jeweils mit einem Erwartungswert E(Xj) und der Varianz V(Xj). Die Zufallsvariablen sind zudem paarweise korreliert mit der Kovarianz  .
.Die Verteilung ist nun die gemeinsame Wahrscheinlichkeit, dass alle Xj höchstens gleich einer jeweiligen Konstanten xj sind, also
 .
.
Multivariate Zufallsvariablen werden i.A. in einem Zufallsvektor
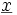 zusammengefasst:
zusammengefasst: .
.
Die Verteilung ist somit
 .
.
Die Erwartungswerte befinden sich im Erwartungswertvektor
der meist mit
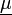 bezeichnet wird.
bezeichnet wird.Die Varianzen werden zusammen mit den Kovarianzen in der (
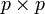 )-Kovarianzmatrix Σ aufgeführt:
)-Kovarianzmatrix Σ aufgeführt:Σ ist symmetrisch mit den Varianzen auf der Hauptdiagonalen.
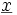 ist also verteilt mit dem Erwartungswertvektor
ist also verteilt mit dem Erwartungswertvektor  und der Kovarianzmatrix Σ.
und der Kovarianzmatrix Σ.Die Umformung zu den Korrelationskoeffizienten
ergibt im Falle positiver Varianzen die Korrelationsmatrix
Gemeinsame Wahrscheinlichkeiten sind häufig schwierig zu berechnen, vor allem, wenn schon die Einzelwahrscheinlichkeiten nicht analytisch bestimmbar sind. Man behilft sich dann gegebenenfalls mit Abschätzungen. Vor allem können die Auswirkungen der Kovarianz auf die Verteilung in der Regel nicht abgesehen werden.
Sind die Zufallsvariablen stochastisch unabhängig, ist die gemeinsame Verteilung gleich dem Produkt der entsprechenden Einzelverteilungen, den Rand- oder auch Marginalverteilungen.
 .
.
Ausgewählte multivariate Verteilungen
Von Bedeutung sind vor allem die
- multivariate Normalverteilung,
- Hotelling t-Verteilung als multivariate t-Verteilung,
- Wishart-Verteilung als multivariate Chi-Quadrat-Verteilung,
die multivariaten Verfahren zu Grunde liegen. Meistens ist es möglich, mittels einer linearen Transformation den Zufallsvektor in ein Skalar umzuwandeln, das dann univariat verteilt ist und so als Testprüfgröße fungiert.
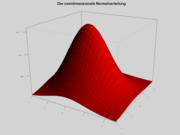
Die multivariate Normalverteilung
Gegeben ist ein Vektor
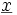 aus p gemeinsam normalverteilten Zufallsvariablen mit dem Erwartungswertvektor μ und der Kovarianzmatrix Σ mit Determinante | Σ | , d. h. die gemeinsame Dichtefunktion der Vektorkomponenten sei gegeben durch
aus p gemeinsam normalverteilten Zufallsvariablen mit dem Erwartungswertvektor μ und der Kovarianzmatrix Σ mit Determinante | Σ | , d. h. die gemeinsame Dichtefunktion der Vektorkomponenten sei gegeben durch .
.
Wir schreiben:
-
 .
.
Die Kovarianzmatrix Σ ist positiv semidefinit. Die Werte der Verteilungsfunktion F müssen numerisch ermittelt werden.
Die multivariate Normalverteilung hat spezielle Eigenschaften:
- Sind die Komponenten des Zufallsvektors
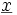 paarweise unkorreliert, sind sie auch stochastisch unabhängig.
paarweise unkorreliert, sind sie auch stochastisch unabhängig.
- Die lineare Transformation
 mit B als
mit B als 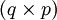 -Matrix
-Matrix 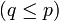 und
und 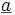 als Vektor der Länge q ist q-dimensional normalverteilt als
als Vektor der Länge q ist q-dimensional normalverteilt als 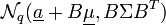 .
.
- Die lineare Transformation
-
- standardisiert den Zufallsvektor x. Es ist
-
 .
.
- also sind die Komponenten von y stochastisch unabhängig.
- X kann auch eine singuläre Kovarianzmatrix besitzen. Man spricht dann von einer degenerierten oder singulären multivariaten Normalverteilung.
Beispiel für eine multivariate Normalverteilung
Betrachtet wird eine Apfelbaumplantage mit sehr vielen gleich alten, also vergleichbaren Apfelbäumen. Man interessiert sich für die Merkmale Größe der Apfelbäume, die Zahl der Blätter und die Erträge. Es werden also die Zufallsvariablen definiert:
X1: Höhe eines Baumes [m]; X2: Ertrag [100 kg]; X3: Zahl der Blätter [1000 Stück].
Die Variablen sind jeweils normalverteilt wie
- X1˜N(4;1);X2˜N(20;100);X3˜N(20;225);
Die meisten Bäume sind also um 4 ± 1m groß, sehr kleine oder sehr große Bäume sind eher selten. Bei einem großen Baum ist der Ertrag tendenziell größer als bei einem kleinen Baum, aber es gibt natürlich hin und wieder einen großen Baum mit wenig Ertrag. Ertrag und Größe sind korreliert, die Kovarianz beträgt Cov(X1,X2) = 9 und der Korrelationskoeffizient ρ12 = 0,9.
Ebenso ist
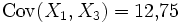 mit dem Korrelationskoeffizienten ρ13 = 0,85, und
mit dem Korrelationskoeffizienten ρ13 = 0,85, und 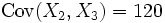 mit dem Korrelationskoeffzienten ρ23 = 0,8.
mit dem Korrelationskoeffzienten ρ23 = 0,8.Fasst man die drei Zufallsvariablen im Zufallsvektor
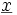 zusammen, ist
zusammen, ist 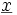 multivariat normalverteilt mit
multivariat normalverteilt mitund
 .
.
Die entsprechende Korrelationsmatrix ist
 .
.
Stichproben bei multivariaten Verteilungen
In der Realität werden in aller Regel die Verteilungsparameter einer multivariaten Verteilung nicht bekannt sein. Diese Parameter müssen also geschätzt werden.
Man zieht eine Stichprobe vom Umfang n. Jede Realisation
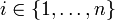 des Zufallsvektors
des Zufallsvektors 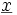 könnte man als Punkt in einem p-dimensionalen Hyperraum auffassen. Man erhält so die
könnte man als Punkt in einem p-dimensionalen Hyperraum auffassen. Man erhält so die 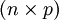 -Datenmatrix X als
-Datenmatrix X als ,
,
die in jeder Zeile die Koordinaten eines Punktes enthält.
Der Erwartungswertvektor wird geschätzt durch den Mittelwertvektor der p arithmetischen Mittelwerte
mit den Komponenten
 .
.Für die Schätzung der Kovarianzmatrix erweist sich die bezüglich der arithmetischen Mittelwerte zentrierte Datenmatrix X * als nützlich. Sie berechnet sich als
 ,
,
mit den Elementen
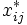 , wobei
, wobei 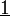 einen Spaltenvektor der Länge n mit lauter Einsen darstellt.
einen Spaltenvektor der Länge n mit lauter Einsen darstellt.Die
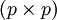 -Kovarianzmatrix hat die geschätzten Komponenten
-Kovarianzmatrix hat die geschätzten Komponenten .
.
Sie ergibt sich als
 .
.
Die Korrelationsmatrix R wird geschätzt durch die paarweisen Korrelationskoeffizienten
 ,
,
auf ihrer Hauptdiagonalen stehen Einsen.
Beispiel zu Stichproben
Es wurden 10 Apfelbäume zufällig ausgewählt. Die 10 Beobachtungen werden in der Datenmatrix X zusammengefasst:
 .
.
Die Mittelwerte berechnen sich, wie beispielhaft an
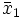 gezeigt, als
gezeigt, als .
.
Sie ergeben den Mittelwertvektor
Für die zentrierte Datenmatrix X * erhält man die zentrierten Beobachtungen, indem man von den Spalten den entsprechenden Mittelwert abzieht:
3,3 - 4,9 = -1,6; 24 – 40 = -16; 27 - 49 = -22 4,9 - 4,9 = 0; 41 - 40 = 1; 55 - 49 = 6 ... ,
also
 .
.
Man berechnet für die Kovarianzmatrix die Kovarianzen, wie im Beispiel,
und entsprechend die Varianzen
 ,
,
so dass sich die Kovarianzmatrix
ergibt.
Entsprechend erhält man für die Korrelationsmatrix zum Beispiel
bzw. insgesamt
 .
.
Literatur
- Mardia, KV, Kent, JT, Bibby, JM: Multivariate Analysis, New York 1979
- Fahrmeir, Ludwig, Hamerle, Alfred, Tutz, Gerhard (Hrsg): Multivariate statistische Verfahren, New York 1996
- Hartung, Joachim, Elpelt, Bärbel: Multivariate Statistik, München, Wien 1999
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.