Kreissektorendiagramm

William Playfairs Kreisdiagramm in seinem Statistical Breviary

Ein Kreisdiagramm (auch Kuchen- bzw. Tortendiagramm) ist eine Darstellungsform für Teilwerte eines Ganzen als Teile eines Kreises.

Das Kreisdiagramm ist kreisförmig und in mehrere Kreissektoren eingeteilt, wobei jeder Kreissektor einen Teilwert und der Kreis somit die Summe der Teilwerte (das Ganze) darstellt. Die Kreissektoren werden jeweils durch Radiuslinien, vom Rand zur Mitte, definiert. Der Mittelpunktswinkel zwischen zwei benachbarten Radiuslinien bestimmt die Größe der Kreissektor. Die jeweilige Sektorgröße (als Winkel) wird folgendermaßen errechnet:

$\mathrm{Winkel} =\frac{360^\circ \cdot \mathrm{Teilwert}}{\mathrm{Gesamtwert}}$

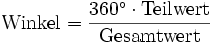
Der Radius des Kreises ist beliebig; die berechneten Winkel bleiben gleich.

Zur besseren Unterscheidung der jeweiligen Sektoren werden verschiedene Farben, Muster und Schattierungen verwendet.

Kreisdiagramme eignen sich besonders für die Darstellung von Verteilungen und Anteilen. Die Anzahl der Teilwerte sollte nicht mehr als 10 betragen; sonst wird das Diagramm unübersichtlich. Mehrere kleine Teilwerte werden ebenso unübersichtlich dargestellt. In diesem Fall empfiehlt sich, die kleinen Teilwerte zu einem "Sonstige"-Wert zusammenzufassen. Gewöhnlich nimmt die Übersichtlichkeit zu, wenn die Teilwerte im Uhrzeigersinn der Größe nach sortiert sind und der größte Teilwert, wie bei einer Uhr, auf der 12-Uhr-Linie beginnt.

Mit einer Tabellenkalkulation lassen sich solche Kreisdiagramme leicht erstellen.

Die alternative Benennung als Kuchen- oder Tortendiagramm bezieht sich auf Schnitte eines runden Kuchens, die den Kreissektoren entsprechen.

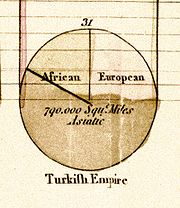
Die Erfindung des Kreisdiagramms wird dem schottischen Ingenieur und Volkswirt William Playfair (1759-1823) zugeschrieben. Dieser verwendete diese Diagrammform im Jahre 1801 in seiner Veröffentlichung 'The Statistical Breviary'.

Beispiel

Kreisdiagramm

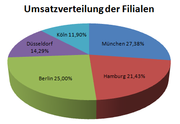
Die folgende Tabelle zeigt die Umsätze eines Filialunternehmens. Mit einem Kreisdiagramm lassen sich diese Werte leichter erfassen und darstellen.

Filiale	Umsatz	Winkel
Köln	100.000,-	42,86°
Düsseldorf	120.000,-	51,43°
Berlin	210.000,-	90,00°
Hamburg	180.000,-	77,14°
München	230.000,-	98,57°
Gesamt	840.000,-	360,00°

Beschriftung

Die Beschriftung kann auf mehrere Arten erfolgen:

• innerhalb des Kreisektors
• außerhalb des Kreissektors; oft mit einer Hilfslinie vom Text zum Kreissektor
• in einer zusätzlichen Legende, welche die im Kreis benutzten Farben oder Schattierungen beschreibt

Oft findet man mehrere Beschriftungsarten in einem Kreisdiagramm. Da bei kleinen Teilwerten kein Platz innerhalb der Sektoren für die Beschriftung ist, muss diese zwingend außerhalb erfolgen.

3D-Effekt

Verzerrte Darstellung, bei der sich die Flächen nicht mehr vergleichen lassen

Computerprogramme erlauben die Anzeige jedes Kreisdiagramms mit einem 3D-Effekt. Dieser Effekt mag grafisch imposanter wirken als die "nüchterne" 2D-Darstellung, hat aber den Nachteil einer verzerrenden Wirkung. Der Kreis wird zu einer Ellipse gestaucht; dadurch werden die für den Betrachter sichtbaren Flächen an den Hauptscheiteln größer, an den Nebenscheiteln kleiner.

Nachteile

Kreisdiagramme werden selten in wissenschaftlicher Literatur, dafür um so mehr in der Betriebs- und Volkswirtschaft verwendet. Ein Grund dafür besteht darin, dass es für den Menschen grundsätzlich schwierig ist, verschieden geformte Flächen zu vergleichen. Dieser Umstand wird durch die Stevenssche Potenzfunktion beschrieben.

Variationen

Halbkreisdiagramm

Ringdiagramm

Teilexplodiertes Kreisdiagramm

Unvollständiger Kreis

Unvollständige Kreise, d. h. weniger als 360 Grad, werden ebenfalls zur Darstellung verwendet. So findet man oft ein Halbkreisdiagramm bei Mehrheitsverhältnissen eines Plenums bei Institutionen. Diese Art der Darstellung bezieht sich auf die Anordnung der Stühle.

Ringdiagramm

Das Ringdiagramm ist eine Abart, bei dem nicht ein komplett ausgefüllter Kreis, sondern ein Ring die Darstellung übernimmt. Zusätzlich können durch Verschachtelung der Ringe mehrere Datenreihen angezeigt werden. Der in der Mitte des Kreises entstandene Platz wird oft zur Kommentierung genutzt.

Explodiertes Kreisdiagramm

Explodierte Kreisdiagramme werden verwendet, um die Aufmerksamkeit auf einen bestimmten Teil zu ziehen. Dieser Effekt ist ebenso bei Ringdiagrammen möglich.

Weblinks