Ellipse

Ellipse geometrisch

Die Saturnringe erscheinen elliptisch.

Eine Ellipse ist eine spezielle geschlossene ovale Kurve. Sie zählt neben dem Punkt, dem Kreis, der Parabel und der Hyperbel zu den Kegelschnitten.

In der Natur treten Ellipsen in Form von ungestörten keplerschen Planetenbahnen um die Sonne auf. Auch beim Zeichnen von Schrägbildern werden häufig Ellipsen benötigt, da ein Kreis durch eine Parallelprojektion im Allgemeinen auf eine Ellipse abgebildet wird.

Die Ellipse (von gr. ἔλλειψις, élleipsis, Mangel) wurde von Apollonios von Perge eingeführt und benannt, die Bezeichnung bezieht sich auf die Exzentrizität ε < 1.^[1]

Definitionen und Begriffe

Diese Grafik zeigt die im nachfolgenden Text verwendeten Bezeichnungen auf.

Es gibt verschiedene Möglichkeiten, Ellipsen zu definieren. Neben der Definition über gewisse Abstände von Punkten ist es auch möglich, eine Ellipse als Schrägbild eines Kreises oder als Schnittlinie zwischen einer entsprechend geneigten Ebene und einem Kreisdoppelkegel zu bezeichnen.

Ellipse als Punktmenge

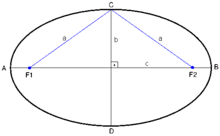
Eine Ellipse kann definiert werden als die Menge aller Punkte P der Ebene, für die die Summe der Abstände zu zwei gegebenen Punkten F₁ und F₂ gleich ist. Die Punkte F₁ und F₂ heißen Brennpunkte.

$E = \left\{P \mid \overline{F_1 P} + \overline{F_2 P} = const\right\}.$

Scheitel und Achsen

Die Achse durch die beiden Brennpunkte heißt Hauptachse und wird durch den Mittelpunkt M in seine zwei großen Halbachsen MS₁ und MS₂ geteilt. Die Punkte S₁ und S₂ heißen Hauptscheitel. Die Länge je einer der beiden großen Halbachsen wird mit a bezeichnet:

$a = \overline{M S_1} = \overline{M S_2}.$

Analog dazu spricht man von den Nebenscheiteln S₃ und S₄und der Nebenachse, bestehend aus den kleinen Halbachsen MS₃ und MS₄. Die Länge der kleinen Halbachsen wird mit b bezeichnet:

$b = \overline{M S_3} = \overline{M S_4}.$

Haupt- und Nebenachse sind rechtwinklig zueinander und schneiden sich im Punkt M.

Spezielle Abstände

Definition der Ellipse als Punktmenge: Die Strecke von einem Brennpunkt zum Rand der Ellipse und weiter zum zweiten Brennpunkt ist immer gleich lang.

Die Definitionsgleichung zusammen mit Symmetrieüberlegungen ergeben, dass der Abstand der Nebenscheitel S₃ und S₄ von den Brennpunkten F₁ und F₂ gerade gleich der Größe a aus der Definition ist:

$\overline{F_1 S_3} = \overline{F_2 S_3} = \overline{F_1 S_4} = \overline{F_2 S_4} = a$

• Nach Symmetrieüberlegungen gilt $\overline{F_1 S_1} = \overline{F_2 S_2}$

$\begin{align} \overline{F_1 S_1} + \overline{F_2 S_1} &= \overline{F_1 S_1} + \overline{F_2 F_1} + \overline{F_1 S_1}\\ &= \overline{S_1 F_1} + \overline{F_1 F_2} + \overline{F_2 S_2}\\ &= 2a.\\ \end{align}$

Das bedeutet, dass die Punktmenge konkret als

$E = \left\{P \mid \overline{F_1 P} + \overline{F_2 P} = 2a\right\}$

angegeben werden kann.

Die halbe Länge p einer Ellipsensehne, die durch einen Brennpunkt geht und zur Hauptachse senkrecht verläuft, nennt man den Halbparameter, manchmal auch nur Parameter p oder auch semi-latus rectum (die Hälfte des latus rectum = 2 · p) der Ellipse:

$p = \tfrac{b^2}a$

Exzentrizität

Ellipse als Kegelschnitt

Hauptartikel: Exzentrizität (Mathematik)

Der Abstand der Brennpunkte vom Mittelpunkt heißt lineare Exzentrizität und wird mit e bezeichnet. Die lineare Exzentrizität berechnet sich über das rechtwinklige Dreieck Δ M F₁ S₃ mit dem Satz des Pythagoras:

$e = \sqrt{a^2-b^2}.$

Neben der linearen Exzentrizität e wird oft auch die dimensionslose numerische Exzentrizität verwendet:

$\varepsilon = \frac ea = \frac{\sqrt{a^2-b^2}}a \in[0,1)$

daraus folgt:

$b = a \sqrt{1 - \varepsilon^2}$

$p = a \cdot (1 - \varepsilon^2)$

• Ist a = b, so ist ε = 0 und die Ellipse ein Kreis.
• Ist a groß gegen b, so ist ε annähernd Eins und damit einer Parabel sehr nahe.

Ellipse als Kegelschnitt

Die Ellipse kann auch als ein Kegelschnitt angesehen werden, der entsteht, wenn der Schnittwinkel zwischen Ebene und Kegelachse größer als der halbe Öffnungswinkel des Doppelkegels ist.

Ellipse als verzerrter Kreis

Eine andere Definition der Ellipse benutzt eine spezielle geometrische Abbildung, nämlich die perspektive Affinität. Hier ist die Ellipse als perspektiv affines Bild eines Kreises definiert. Dabei wird jeder Kreisdurchmesser auf einen Ellipsendurchmesser abgebildet.

Hauptlage und analytische Definition

Eine Ellipse, deren Mittelpunkt im Koordinatenursprung liegt und deren Hauptachse mit der X-Achse zusammenfällt, nennt man Ellipse in der 1. Hauptlage. Es gilt die Gleichung

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

für die Koordinaten der Ellipsenpunkte einer solchen Ellipse.

Eigenschaften

Brennpunkteigenschaft

Hauptartikel: Brennpunkt (Ellipse)

Brennpunktseigenschaft

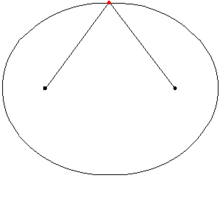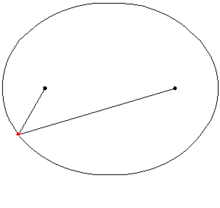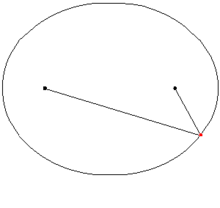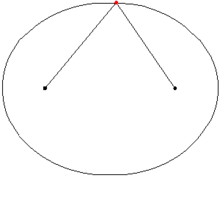
Die Verbindungslinie zwischen einem Brennpunkt und einem Punkt der Ellipse heißt Brennlinie, Leitstrahl, oder Brennstrahl. Ihren Namen erhielten Brennpunkte und Brennstrahlen aufgrund der Eigenschaft, dass der Winkel zwischen den beiden Brennstrahlen in einem Punkt der Ellipse durch die Normale in diesem Punkt halbiert wird. Damit ist der Einfallswinkel, den der eine Brennstrahl mit der Tangente bildet, gleich dem Ausfallswinkel, den die Tangente mit dem anderen Brennstrahl bildet. Ein Lichtstrahl, der von einem Brennpunkt ausgeht, würde demnach an der Ellipsentangente so reflektiert, dass er den anderen Brennpunkt trifft. Bei einem ellipsenförmigen Spiegel treffen sich demnach alle von einem Brennpunkt ausgehenden Lichtstrahlen in dem anderen Brennpunkt.

Da der Weg von einem zum anderen Brennpunkt (entlang zweier zusammengehöriger Brennstrahlen) immer gleich lang ist, wird z. B. Schall nicht nur „verstärkt“ (siehe unten) von einem zum anderen Brennpunkt übertragen, sondern kommt sogar zeit- und phasengleich (also verständlich und nicht interferierend) dort an.

Zwei Ellipsen mit übereinstimmenden Brennpunkten nennt man konfokal.

Eine Ellipse, deren zwei Brennpunkte zu einem zusammenfallen, wird dabei zum Kreis (entspricht verschwindender Exzentrizität, s. o.).

Natürliches Vorkommen und Anwendung in der Technik

Die Decken mancher Höhlen ähneln einer Ellipsenhälfte. Befindet man sich in einem Brennpunkt dieser Ellipse, hört man jedes Geräusch, dessen Ursprung im zweiten Brennpunkt liegt, verstärkt („Flüstergewölbe“). Diese Art der Schallübertragung funktioniert in einigen Stationen der Pariser Métro sogar von Bahnsteig zu Bahnsteig. Das gleiche Prinzip der Schallfokussierung wird heute zur Zertrümmerung von Nierensteinen mit Stoßwellen verwendet. Auch im lampengepumpten Nd:YAG-Laser wird ein Reflektor in Form einer Ellipse verwendet. Die Pumpquelle – entweder eine Blitzlampe oder eine Bogenlampe – wird in dem einen Brennpunkt positioniert, und der dotierte Kristall wird in den anderen Brennpunkt gelegt.

Ellipse mit Leitlinien

Direktrix

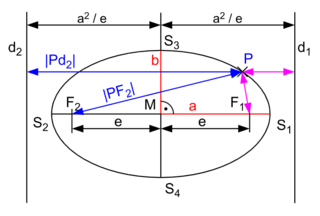
Eine Parallele zur Nebenachse im Abstand a²/e bezeichnet man als Direktrix oder Leitlinie. Für einen beliebigen Punkt P der Ellipse ist das Verhältnis seines Abstands von einem Brennpunkt zu dem Abstand von der Direktrix d auf der entsprechenden Seite der Nebenachse gleich der numerischen Exzentrizität:

$\mathrm{\left|P F_1\right| : \left|P d_1\right| = \left|P F_2\right| : \left|P d_2\right| = \varepsilon}.$

Ein gegebener Brennpunkt F, eine Gerade d (die Direktrix) und eine Zahl

$0 \leq \varepsilon < 1$

definieren umgekehrt eine Ellipse E als Menge aller Punkte P für die das Verhältnis ihres Abstandes

$\left| FP \right|$

vom Brennpunkt zu ihrem Abstand

$\left| Fd \right|$

von der Geraden d gleich ε ist.

Konjugierte Durchmesser

Ellipse mit zwei konjugierten Durchmessern

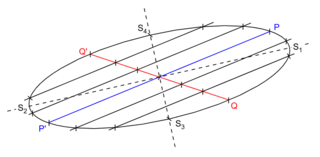
Betrachtet man zu einem beliebigen Ellipsendurchmesser (einer Ellipsensehne durch den Ellipsenmittelpunkt) PP' alle parallelen Sehnen, so liegen deren Mittelpunkte ebenfalls auf einem Ellipsendurchmesser QQ'. Man nennt QQ' den zu PP' konjugierten Durchmesser. Bildet man zum konjugierten Durchmesser erneut den konjugierten Durchmesser, so erhält man wieder den ursprünglichen Ellipsendurchmesser. In der Zeichnung stimmt also der zu QQ' konjugierte Durchmesser mit dem ursprünglichen Durchmesser PP' überein.

Konstruktion

Näherung über Krümmungskreise

Ellipsen lassen sich (mit Zirkel und Lineal) nur punktweise konstruieren, d. h. eine genaue Konstruktion wie zum Beispiel beim Kreis ist unmöglich. Mit Hilfe der Krümmungskreise an den Scheitelpunkten und eines Kurvenlineals lässt sich aber auch zeichnerisch ein relativ genaues Bild der Ellipse erstellen. Um aber zum Beispiel eine Gerade exakt mit einer Ellipse zu schneiden, braucht man besondere Konstruktionstechniken, welche die Eigenschaften der Ellipse ausnutzen.

Gärtnerkonstruktion

Gärtnerkonstruktion einer Ellipse

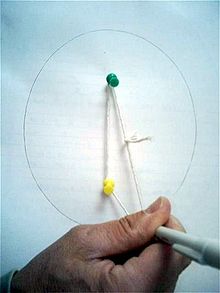
Eine einfache Möglichkeit, die Ellipse genau zu zeichnen, ist die sogenannte Gärtnerkonstruktion. Sie benutzt direkt die Ellipsendefinition: Um ein ellipsenförmiges Blumenbeet zu erstellen, schlägt man zwei Pflöcke in die Brennpunkte und befestigt daran die Enden einer Schnur mit der Länge 2a. Nun spannt man die Schnur und fährt mit einem Markierungsgerät an ihr entlang. Da diese Methode neben Zirkel und Lineal zusätzliche Hilfsmittel benötigt, handelt es sich nicht um eine Konstruktion der klassischen Geometrie.

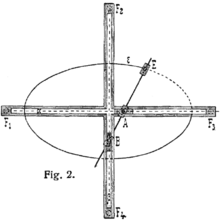
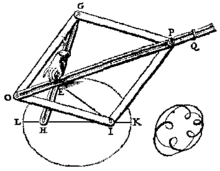
Ellipsenzirkel

Ellipsenzirkel

Ellipsenzirkel nach Frans van Schooten aus dem 17. Jahrhundert

Ebenfalls können Ellipsen mit Frans van Schootens Ellipsenzirkel oder darauf beruhenden Nachbauten konstruiert werden. Der Gelenkmechanismus wurde von dem holländischen Mathematiker im 17. Jahrhundert erfunden. Wenn man am Stift in Punkt E zieht, zeichnet dieser eine Ellipse. Der Mechanismus ist an den Brennpunkten H und I auf der Zeichenunterlage befestigt.

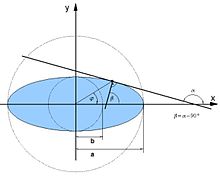
Konstruktion nach de la Hire

Mittels der Ellipsenkonstruktion nach de la Hire (auch Konstruktion nach Proklus) können Ellipsenpunkte konstruiert werden, ohne dass die Brennpunkte bekannt sein müssen. Man zeichne zwei konzentrische Kreise mit den Radien b (Innen- oder Nebenkreis) und a (Außen- oder Hauptkreis) und zusätzlich eine vom Zentrum ausgehende Linie mit der Steigung tan(t), die beide Kreise schneidet. Die Parallele zur X-Achse durch den Schnittpunkt auf dem Nebenkreis trifft im Punkt P die Parallele zur Y-Achse durch den Schnittpunkt auf dem Hauptkreis. Ändern des Polarwinkels t lässt P der Kontur der Ellipse mit den Halbachsen a und b folgen.

Rytzsche Achsenkonstruktion

Sind zwei konjugierte Durchmesser gegeben, können mit Hilfe der Rytzschen Achsenkonstruktion die Haupt- und Nebenscheitel (und die Achsen) bestimmt werden.

Auf Basis eines Kreises

Besonders in der Computergrafik lohnt sich die Ableitung einer Ellipse aus einer Kreisform. Eine achsenparallele Ellipse ist dabei einfach ein Kreis, der in einer der Koordinatenrichtungen gestaucht bzw. gedehnt, in anderen Worten anders skaliert wurde. Eine allgemeine, in beliebigem Winkel gedrehte Ellipse kann man aus so einer achsenparallelen Ellipse durch Scherung erhalten, s. a. Bresenham-Algorithmus.

Radlinien

• Cardanische Kreise: Ein rollender Kreis auf einer Ebene lässt sich als Ellipsenzirkel verwenden. Die elliptische Kurve entsteht, wenn man dabei den Weg eines Randpunktes des rollenden Kreises verfolgt.
• Ein Kreis wird innerhalb eines doppelt so großen Kreises abgerollt. Animation

Beispiele

• Schaut man schräg auf einen Kreis (beispielsweise auf die Deckfläche eines Kreiszylinders), so erscheint dieser Kreis als Ellipse. Präziser: Eine Parallelprojektion bildet Kreise im Allgemeinen auf Ellipsen ab.

• In der Astronomie kommen Ellipsen häufig als Bahnen von Himmelskörpern vor. Nach dem ersten keplerschen Gesetz bewegt sich jeder Planet auf einer Ellipse um die Sonne, wobei diese in einem der beiden Brennpunkte steht. Entsprechendes gilt für die Bahnen von wiederkehrenden (periodischen) Kometen, Planetenmonden oder Doppelsternen. Allgemein ergeben sich bei jedem Zweikörperproblem der Gravitationskraft zueinander ähnliche Ellipsenbahnen, wenn die Energie nicht ausreicht, die Entfernung der beteiligten Himmelskörper unendlich groß werden zu lassen.

• Für jeden zwei- oder dreidimensionalen harmonischen Oszillator erfolgt die Bewegung auf einer Ellipsenbahn. So schwingt etwa der Pendelkörper eines Fadenpendels näherungsweise auf einer elliptischen Bahn, falls die Bewegung nicht auf eine Ebene beschränkt ist.

Formelsammlung

Ellipsengleichung (kartesische Koordinaten)

Mittelpunkt (0|0),

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$

Mittelpunkt (x₀|y₀), Hauptachse parallel zur X-Achse:

$\frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1.$

Herleitung

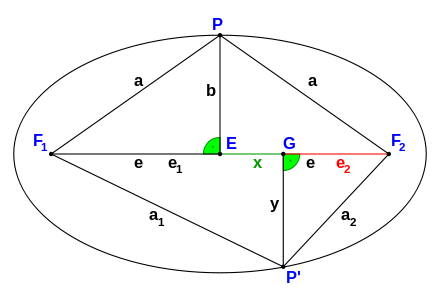
Um die Ellipsengleichung herzuleiten (Mittelpunkt (0|0)), stellt man sich zuerst mit Hilfe des nebenstehenden Bildes folgendes Gleichungssystem auf:

(1) 2a = a₁ + a₂

(2) $y^2=a_1^2-(e+x)^2$

(3) $y^2=a_2^2-(e-x)^2$

(4) a² = b² + e²

Formel (1) ist hierbei ein direktes Resultat der Ellipsendefinition. Nach y² aufgelöst, wobei a₁, a₂ und e eliminiert werden, erhält man:

$y^2 = b^2 \left(1-\frac{x^2}{a^2} \right)$

Wenn man nun alle Variablen auf eine Seite bringt, erhält man obige Gleichung für die Ellipse.

Praktisch, um aus den zwei Bahnelementen numerische Exzentrizität und große Halbachse eine Planetenbahn als Graph darzustellen, ist folgende Funktion. Man erhält sie, wenn man (4) verändert in ε=e/a und dann nach y² auflöst:

$y^2=(a^2-x^2) \cdot (1-\epsilon^2) = \frac{(a^2-e^2)(a^2-x^2)}{a^2}$

Ellipsengleichung (Parameterform)

Mittelpunkt (0|0), Hauptachse als X-Achse:

$\begin{pmatrix} x\\ y \end{pmatrix}=\begin{pmatrix} a\cos t\\ b\sin t \end{pmatrix} \quad \text{mit} \quad 0\le t\le 2\pi.$

Mittelpunkt (x₀|y₀), Hauptachse parallel zur X-Achse:

$\begin{pmatrix} x\\ y \end{pmatrix}=\begin{pmatrix} x_0+a\cos t\\ y_0+b\sin t \end{pmatrix} \quad \text{mit} \quad 0\le t\le 2\pi.$

Mittelpunkt (x₀|y₀), Hauptachse um φ bezüglich X-Achse rotiert:

$\begin{pmatrix} x\\ y \end{pmatrix}=\begin{pmatrix} x_0 + a\cos t\,\cos \varphi - b\sin t\,\sin\varphi\\ y_0 + a\cos t\,\sin \varphi + b\sin t\,\cos\varphi \end{pmatrix} \quad \text{mit} \quad 0\le t\le 2\pi.$

Dabei bezeichnet t den Parameter dieser Darstellung.

Ellipsengleichung (Polarkoordinaten)

Hauptachse waagrecht, Mittelpunkt als Pol, Polarachse längs Hauptachse nach rechts:

$r = \frac b{\sqrt{1 - \varepsilon^2 \cos^2 \varphi}},$

Hauptachse waagrecht, rechter Brennpunkt als Pol, Polarachse längs Hauptachse nach rechts (Halbparameter p):

$r = \frac p{1 + \varepsilon \cos \varphi},$

Hauptachse waagrecht, linker Brennpunkt als Pol, Polarachse längs Hauptachse nach rechts:

$r = \frac p{1 - \varepsilon \cos \varphi}.$

Tangentengleichung (kartesische Koordinaten)

Mittelpunkt (0|0), Hauptachse als X-Achse, Berührpunkt (x_B|y_B):

$\frac{x_B x}{a^2} + \frac{y_B y}{b^2} = 1$

Mittelpunkt (x₀|y₀) Hauptachse parallel zur X-Achse, Berührpunkt (x_B|y_B):

$\frac{(x_B - x_0) (x - x_0)}{a^2} + \frac{(y_B - y_0) (y - y_0)}{b^2} = 1$

Beziehung zwischen Polar- und Normalenwinkel

Die Winkel der Ellipsentangente

In der nebenstehenden Grafik gilt die Winkelrelation

$\varphi = \arctan \left( (1 - \varepsilon^2 ) \tan(\beta)\right)$

und nachdem man die Formel für ε eingesetzt hat:

$\varphi = \arctan \left(\frac {b^2}{a^2} \tan(\beta)\right)$

Herleitung

Der Zusammenhang des Polarwinkels φ und dem Steigungswinkel der Normalen β (siehe Grafik rechts) lässt sich z.B. so finden:

Auflösen der Tangentengleichung nach y ergibt die Tangentensteigung tan(α) als Koeffizient von x zu

$\tan(\alpha )=-\tfrac{b^2}{a^2}\cdot\tfrac{x_B}{y_B}$,

also gilt mit

$\tan(\varphi) =\tfrac{ y_B}{x_B}$

und

$\tan(\alpha)=-\frac{1}{\tan(\beta )}$

die Beziehung

$-\frac{1}{\tan(\beta)} = -\frac{b^2}{a^2}\cdot \frac{1}{\tan(\varphi)}.$

Daraus folgt mit Auflösen erst nach tan(φ) und anschließend nach φ der gesuchte Zusammenhang.

Normalengleichung (kartesische Koordinaten)

Mittelpunkt (0|0), Hauptachse als X-Achse, Berührpunkt (x_B|y_B):

$\left( 1-{\frac {y}{y_B}} \right) \frac {b^2}{a^2}+{\frac {x}{x_B}}=1$

oder auch

$b^2 \left( \frac {y}{y_B} - 1 \right) = a^2 \left( \frac {x}{x_B} - 1 \right)$

Krümmungsradien

Krümmungsradius in einem der beiden Hauptscheitel:

$r_\mathrm{H} = \tfrac{b^2}{a},$

Krümmungsradius in einem der beiden Nebenscheitel:

$r_\mathrm{N} = \tfrac{a^2}{b}.$

Weitere Formeln

Flächeninhalt

Mit den Halbachsen a und b:

$A = \pi a b = \pi a^2 \sqrt{1-\varepsilon^2}.$

In Polarkoordinaten lässt sich auch der Flächeninhalt als Funktion des (Polar-)Winkels φ darstellen: (Polarkoordinaten: Hauptachse waagrecht, Mittelpunkt als Pol, Polarachse längs Hauptachse nach rechts):

Für einen Ellipsensektor mit dem Winkel

$\varphi\in [0,2 \pi]$

erhält man:

$A = \frac{a b \varphi}{2}.$

Ist die Ellipse durch eine implizite Gleichung

Ax² + Bxy + Cy² + 1 = 0

gegeben, dann beträgt ihr Flächeninhalt

$A=\frac{2\pi}{\sqrt{ 4 A C - B^2 }}$.

Umfang

Diagramm zur Berechnung des Ellipsenumfangs

Der Umfang einer Ellipse kann nicht exakt durch elementare Funktionen angegeben werden. Er kann nur als Integral dargestellt werden, das daher elliptisches Integral genannt wird.

$U = 4a\int\limits_0^{\frac{\pi}{2}} {\sqrt {1 - \varepsilon^2 (\sin t)^2}} \ \mathrm dt=4a \; E(\varepsilon).$

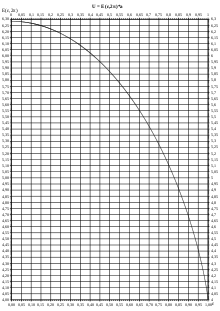
Der Umfang hängt von der numerischen Exzentrizität ε und der großen Halbachse a ab. E(ε) heißt elliptisches Integral und lässt sich nicht durch elementare Funktionen ausdrücken. Mit Hilfe des nebenstehenden Diagramms kann bei gegebener Exzentrizität ε der Wert des Faktors k = 4E(ε) für das Produkt

$U = k \cdot a$

abgelesen werden.

Es gibt die Reihenentwicklung:

$U = 2 a \pi \left( 1 - \sum_{i=1}^\infty \left( \prod_{k=1}^i \frac{2k-1}{2k} \right)^2 \frac{\varepsilon^{2i}}{2i-1} \right)$

$=2a \pi \left[1 - \left(\frac 12\right)^2 \varepsilon^2 - \left(\frac{1 \cdot 3}{2 \cdot 4}\right)^2 \frac{\varepsilon^4}3 - \dotsb - \left(\frac{1 \cdot 3 \cdot 5 \cdots (2n-1)}{2 \cdot 4 \cdot 6 \cdots 2n}\right)^2 \frac{\varepsilon^{2n}}{2n-1} - \dotsb \right]$

und Näherungen z. B.:

$U \approx 2 \pi {\sqrt {\frac{1}2 (a^2+b^2)}} = \pi {\sqrt {2 (a^2+b^2)}}$ (nur auf etwa 10% genau) und

$U \approx \pi (a+b) \left(1+ \frac{3\lambda^2}{10+\sqrt{4-3\lambda^2}} \right)$, wobei $\quad \lambda = \frac{a-b}{a+b}$.

Die letzte Näherung ist in einem weiten ε-Bereich von

$0 \leq \varepsilon \leq 0{,}9$

sehr genau. Der relative Fehler nimmt danach mit zunehmendem ε zu und beträgt:

Bereich	rel. Fehler
0,0000 ≤ ε < 0,8820	<10−9
0,8820 < ε < 0,9242	< 10−8
0,9242 < ε < 0,9577	< 10−7
0,9577 < ε < 0,9812	< 10−6
0,9812 < ε < 0,9944	< 10−5
0,9944 < ε < 0,9995	< 10−4
0,9995 < ε < 1,0000	< 0,000403

→ Siehe auch: Meridianbogen

Die numerische Exzentrizität für eine Ellipse mit der großen Halbachse a und der kleinen Halbachse b ist

$\varepsilon_\text{ellipse}(a,b) = \frac{\sqrt{a^2 - b^2}}{a} = \sqrt{1 - \left( {b\over a} \right) ^2} \quad \text{mit} \quad a \ge b$

Setzt man dieses ε in die obige von a und ε abhängige Integralgleichung ein, so erhält man eine Funktion für den Umfang mit a und b als Argumenten:

$U(a,b) = 4a\int\limits_0^{\frac{\pi}{2}} {\sqrt {1 - \sin^2 t\left(1 - \left( {b\over a} \right) ^2\right)}} \ \mathrm dt \quad \text{mit} \quad a \ge b$

Die Umkehrung, also eine Abbildung, die (für eine gegebene Ellipse) der Bogenlänge einen Winkel zuordnet, ist eine elliptische Funktion.

Siehe auch

• Kreis
• Parabel
• Hyperbel
• Gabriel Lamé verallgemeinerte die Ellipse zur laméschen Kurve (Superellipse).
• Ellipsoid
• Homöoid
• Fokaloid
• Feynmans verschollene Vorlesung: Die Bewegung der Planeten um die Sonne

Einzelnachweise

1. ↑ I. N. Bronstein, K. A. Semendjajew (Begründer), Günter Grosche (Bearb.), Eberhard Zeidler (Hrsg.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart 1996, ISBN 3-8154-2001-6, S. 24.

Weblinks

 Wiktionary: Ellipse – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Commons: Ellipsen – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Ellipse. In: MathWorld. (englisch)

Berechnungen

• Formeln zum Ellipsenumfang mit Beispielrechnung
• Website zum Berechnen eines Ellipsenumfang
• Tangenten und Schnitt mit Gerade (JavaScript)

Konstruktion

Für alle folgenden Links wird ein Java-Plug-in benötigt.

• Webseite mit der Möglichkeit Ellipsenkonstruktionen interaktiv auszuprobieren
• http://www.fh-lueneburg.de/u1/gym03/homepage/faecher/mathe/geometri/analytgeo/ellipsenzirkeleuk.htm
• http://home.eduhi.at/teacher/alindner/geonext/geonext/klasse4/ellipse/ell_zirkel_kreis.htm
• http://www.learn-line.nrw.de/angebote/selma/foyer/projekte/bielefeldproj2/plugin_cin/e_streifenkonstr.htm
• Konstruktion der Ellipse als affines Bild des Kreises – eine Visualisierung mit GeoGebra