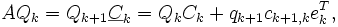Krylov-Zerlegung

In der numerischen Mathematik ist eine Krylow-Zerlegung (nach Alexei Nikolajewitsch Krylow) eine Matrixgleichung der folgenden Gestalt:

$AQ_k=Q_{k+1}\underline{C}_k=Q_kC_k+q_{k+1}c_{k+1,k}e_k^T,$

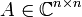wobei $A\in\mathbb{C}^{n\times n}$ eine quadratische Matrix ist, 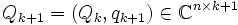$Q_{k+1}=\left(Q_k,q_{k+1}\right)\in\mathbb{C}^{n\times k+1}$ als Spalten die Basisvektoren eines Krylowraumes enthält und 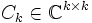$C_k\in\mathbb{C}^{k\times k}$ eine (im Allgemeinen unreduzierte) Hessenbergmatrix ist.

Ferner bezeichnet 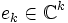$e_k\in\mathbb{C}^k$ den k-ten kanonischen Einheitsvektor und 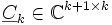$\underline{C}_k\in\mathbb{C}^{k+1\times k}$ ist eine um eine unten angefügte Zeile erweiterte Hessenbergmatrix, wobei nur das letzte Element dieser Zeile ungleich Null ist.

Diese Krylow-Zerlegungen treten in natürlicher Weise bei der algorithmischen Beschreibung von Krylow-Unterraum-Verfahren auf. Der Begriff wurde von Pete Stewart geprägt.