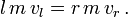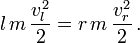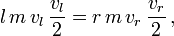- Kugelstosspendel
-
Ein Kugelstoßpendel (auch Kugelpendel, Newtonpendel oder Newton-Wiege) ist eine Anordnung von hintereinander beidseitig aufgehängten Kugeln gleicher Masse und Pendellänge. Wenn man die am weitesten rechts liegende Kugel anhebt und gegen die daneben prallen lässt, wird die am weitesten links liegende Kugel abgestoßen.
Die Vorrichtung geht auf den französischen Physiker Edme Mariotte (1676) zurück. Sie wurde in den 1960er Jahren als kleines, dekoratives Spielzeug beliebt.
Selbstverständlich geht es auch umgekehrt: Man kann also die linke Kugel anheben und loslassen, damit sich die rechte abstößt. Wenn man die zwei rechten Kugeln anhebt und gegen die mittlere prallen lässt, so stoßen sich die beiden linken ab. Auch da ist es natürlich andersherum möglich. Entsprechendes gilt für mehr Kugeln.
Inhaltsverzeichnis
Funktionsweise
Die im nebenstehenden Bild am weitesten links liegende, ruhende Kugel nimmt den Impuls der aufprallenden Kugel auf und gibt ihn an die rechts daneben liegende Kugel ab, jene dann an die rechts daneben und so weiter. Die am weitesten rechts liegende Kugel kann allerdings keinen Impuls mehr weitergeben und wird abgestoßen.
Dabei handelt es sich um elastische Stöße, bei denen die kinetische Energie und der Impuls erhalten bleiben. Da beim Stoß keine äußeren Kräfte in Bewegungsrichtung wirken, muss der Impuls der l Kugeln der Masse m, die mit der Geschwindigkeit vl von links auf die ruhenden Kugeln treffen, gleich dem Impuls der r angestoßenen Kugeln der Masse m sein, die angestoßen werden. Nimmt man weiterhin an, dass die angestoßenen Kugeln sich kollektiv mit der Geschwindigkeit vr nach rechts bewegen, besagt die Impulserhaltung
Weiterhin muss die Energie vor und nach dem Stoß übereinstimmen, wobei man die Energie vernachlässigt, die in Schwingungen der Kugeln geht,
Schreibt man dies als
und berücksichtigt man die erste Gleichung, so sind, da
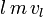 nicht Null ist, die Geschwindigkeiten gleich,
nicht Null ist, die Geschwindigkeiten gleich, 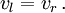 Dann besagt die erste Gleichung l = r: es fliegen so viele Kugeln weg wie auftreffen.
Dann besagt die erste Gleichung l = r: es fliegen so viele Kugeln weg wie auftreffen.Hier wurde angenommen, dass sich die angestoßenen Kugeln alle mit der gleichen Geschwindigkeit wegbewegen und die restlichen ruhen. Dass sie das tun, kann man aber bei mehr als zwei Kugeln nicht aus der Energie- und Impulserhaltung folgern.
Denn wenn im Schwerpunktsystem l Kugeln von links mit Geschwindigkeit vl auf r Kugeln mit Geschwindigkeit vr stoßen, wobei
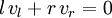 gilt, so ist mit Energie- und Impulserhaltung verträglich, dass nach dem Stoß l Kugeln mit Geschwindigkeit vl nach rechts und r Kugeln mit Geschwindigkeit vr nach links weiterlaufen. Aber auch l Kugeln mit umgedrehter Geschwindigkeit − vl und r Kugeln mit Geschwindigkeit − vr sind möglich.
gilt, so ist mit Energie- und Impulserhaltung verträglich, dass nach dem Stoß l Kugeln mit Geschwindigkeit vl nach rechts und r Kugeln mit Geschwindigkeit vr nach links weiterlaufen. Aber auch l Kugeln mit umgedrehter Geschwindigkeit − vl und r Kugeln mit Geschwindigkeit − vr sind möglich.Zur Erklärung des Verhaltens der Kugelkette muss man genauer bedenken, wie eine Stoßwelle durch die Kette hindurchläuft.
Siehe auch
Literatur
- F. Herrmann, P. Schmälzle: A simple explanation of a well-known collision experiment, Am. J. Phys. 49, 761 (1981)
- F. Herrmann, M. Seitz: How does the ball-chain work?, Am. J. Phys. 50, 977 (1982)
Weblinks
Wikimedia Foundation.