Kinetische Energie

Die kinetische Energie (von griechisch kinesis = Bewegung) oder auch Bewegungsenergie ist die Energie, die ein Objekt aufgrund seiner Bewegung enthält. Sie entspricht der Arbeit, die aufgewendet werden muss, um das Objekt aus der Ruhe in die momentane Bewegung zu versetzen. Sie hängt von der Masse m und von der Geschwindigkeit v des bewegten Körpers ab.

Als Formelzeichen für die kinetische Energie wird in der theoretischen Physik üblicherweise T verwendet, seltener auch E_kin (z. B. in der physikalischen Chemie).

Die Maßeinheit der kinetischen Energie ist Joule.

Das Konzept der kinetischen Energie (noch ohne den Vorfaktor 1/2) wurde im 18. Jahrhundert von Émilie du Châtelet, aufbauend auf Überlegungen von Gottfried Wilhelm Leibniz, eingeführt (als Vis Viva, Lebendige Kraft). Bis zu diesem Zeitpunkt vertrat Newton die Ansicht, die Bewegungsenergie sei der Geschwindigkeit proportional.

Kinetische Energie in der klassischen Mechanik

Massenpunkt

In der klassischen Mechanik ist die kinetische Energie T eines Massenpunktes abhängig von seiner Masse m und seinem Bewegungszustand. Wird der Bewegungszustand durch die Geschwindigkeit v des Massenpunktes beschrieben, so gilt

$T = \frac{1}{2} m v^2.$

In speziellen Koordinatensystemen hat dieser Ausdruck die Form:

• Kartesische Koordinaten (x, y, z):

$T = \frac{1}{2} m \left(\dot x^2 + \dot y^2 + \dot z^2\right)$

• Ebene Polarkoordinaten (r,ϕ):

$T = \frac{1}{2}m \left(\dot r^2 + r^2 \dot \varphi^2 \right)$

• Zylinderkoordinaten (r,ϕ,z):

$T = \frac{1}{2}m \left(\dot r^2 + r^2 \dot \varphi^2 + \dot z^2 \right)$

• Kugelkoordinaten (r,ϕ,θ):

$T = \frac{1}{2}m \left(r^2 \left[\dot \theta^2 + \dot \varphi^2 \sin^2\theta \right] + \dot r^2 \right)$

Dabei bedeutet der Punkt über der Koordinate ihre zeitliche Änderung, die Ableitung nach der Zeit.

In der hamiltonschen Mechanik wird der Bewegungszustand eines Massepunktes nicht durch seine Geschwindigkeit, sondern durch seinen Impuls p ausgedrückt. In diesem Fall gilt:

$T = \frac{p^2}{2m}$

Starre Körper

Die kinetische Energie eines starren Körpers mit der Gesamtmasse M und der Geschwindigkeit v_s seines Schwerpunktes kann separiert werden als die Summe seiner Energie aus der Bewegung seines Schwerpunkts (Translationsenergie) und der Rotationsenergie aus der Drehung um den Schwerpunkt.

$T = \frac{1}{2} M {v_\mathrm{s}}^2 + \frac{1}{2} J_\mathrm{s} \omega^2$

Hier ist J_s das Trägheitsmoment des Körpers bezüglich seines Schwerpunktes und ω seine Winkelgeschwindigkeit.

Mit dem Trägheitstensor I wird dies allgemein geschrieben als

$T = \frac{1}{2} M {v_\mathrm{s}}^2 + \frac{1}{2} \boldsymbol{\omega}^T I \boldsymbol\omega$

Hydrodynamik

In der Hydrodynamik wird oft statt der kinetischen Energie die kinetische Energiedichte angegeben. Diese wird meist durch ein kleines e oder $\epsilon$ ausgedrückt:

$e_\mathrm{kin} = \frac{1}{2} \rho v^2$

Hierbei bezeichnet ρ die Dichte.

Kinetische Energie in der relativistischen Mechanik

Datei:E Kin.jpg

Relativistische und klassische kinetische Energie im Vergleich.

In der relativistischen Physik gilt die oben angegebene Abhängigkeit der kinetischen Energie von der Geschwindigkeit nur näherungsweise für Geschwindigkeiten deutlich kleiner als die Lichtgeschwindigkeit. Aus dem Ansatz, dass die kinetische Energie T die Differenz aus Gesamtenergie und Ruheenergie ist, folgt:

T = m_relc² − mc²,

Dabei ist c die Lichtgeschwindigkeit, m die Ruhemasse und m_rel die relativistische Masse. Mit m_rel = γ · m lautet die Beziehung:

$T = \left(\gamma - 1\right) m c^2$,

γ ist der Lorentzfaktor

$\gamma = \frac{1}{\sqrt{1 - (v/c)^2}}$

Aus der Taylor-Entwicklung nach v / c erhält man

$T \approx \frac{1}{2} m v^2 + \frac{3}{8}\frac{m v^4}{c^2} + \dots$

also für $v \ll c$ wieder die Newtonsche kinetische Energie.

Da die Energie über alle Grenzen wächst, wenn die Geschwindigkeit gegen die Lichtgeschwindigkeit geht, $\lim_{v \to c}T = \infty$, ist es nicht möglich, einen massebehafteten Körper auf Lichtgeschwindigkeit zu beschleunigen.

Das Diagramm rechts zeigt für einen Körper mit der Masse von $m = 1\, \mathrm{kg}$ die relativistische und die Newtonsche kinetische Energie als Funktion der Geschwindigkeit (gemessen in Vielfachen der Lichtgeschwindigkeit).

Da die Geschwindigkeit eines bewegten Körpers vom Bezugssystem abhängt, gilt dies auch für dessen kinetische Energie. Das gilt in Newtonscher und in relativistischer Physik.

Anwendungsbeispiele

Relativistische Geschwindigkeit eines Elektrons im elektrischen Feld.

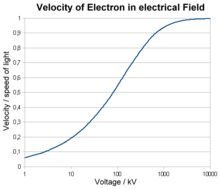
Im elektrischen Feld nimmt die kinetische Energie eines Elektrons der Ladung e und der Ruhemasse m linear mit der Beschleunigungsspannung U zu. Die Gesamtenergie E beträgt:

$E = mc^2 + e \cdot U.$

Eingesetzt in die Beziehung oben (mit E₀=mc²) ergibt sich für die Geschwindigkeit v eines Elektrons:

$v = c \cdot \sqrt{1 - {\left(\frac{E_0}{E}\right)}^2}$

Bei Beschleunigungsspannungen unterhalb 1 kV lässt sich die Geschwindigkeit aus dem klassischen Ansatz für die kinetische Energie abschätzen, bei höheren Energien muss relativistisch gerechnet werden. Bereits bei einer Spannung von 10 kV erreichen die Elektronen eine Geschwindigkeit von fast 20% der Lichtgeschwindigkeit, bei 1 MV 94%.

Der Large Hadron Collider führt Protonen eine Energie von 7 TeV pro Strahl zu. Dem entspricht eine Beschleunigungsspannung von 7 TV. Die Protonen (Ruheenergie 940 MeV) werden auf das 0,999999991-Fache der Lichtgeschwindigkeit beschleunigt.

Kinetische Energie in der Quantenmechanik

In der Quantenmechanik ist der Erwartungswert $\langle\hat{T}\rangle$ der kinetischen Energie eines Teilchens der Masse m, welches durch die Wellenfunktion $\vert\psi\rangle$ beschrieben wird, gegeben durch

$\langle\hat{T}\rangle = \frac{1}{2m}\langle\psi |\hat P^2 | \psi \rangle$,

wobei $\hat P^2$ das Quadrat des Impuls-Operators des Teilchens ist.

Im Formalismus der Dichtefunktionaltheorie ist nur vorausgesetzt, dass die Elektronendichte bekannt ist, das heißt, dass die Wellenfunktion formal nicht bekannt sein muss. Mit der Elektronendichte $\rho(\mathbf{r})$ ist das exakte Funktional der kinetischen Energie für N Elektronen unbekannt; falls jedoch im Fall N = 1 ein einzelnes Elektron betrachtet wird, so kann die kinetische Energie als

$T[\rho] = \int \frac{1}{8}\frac{\nabla \rho(\mathbf{r}) \cdot \nabla \rho(\mathbf{r}) }{ \rho(\mathbf{r}) } \mathrm{d}^3r$

geschrieben werden, wobei T[ρ] das Weizsäcker-Funktional der kinetischen Energie ist.

Siehe auch

• Potentielle Energie
• Energieerhaltungssatz
• Kinetische Energie in der Geografie: Schleppkraft