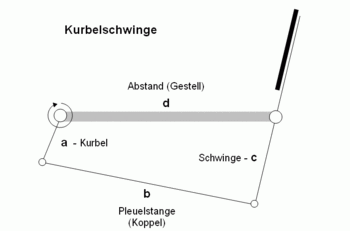
Kurbelschwinge

Die Kurbelschwinge (auch "Kurbelgetriebe") gehört zu den Koppelgetrieben - Getriebe, die Drehbewegungen in geradlinige oder schwingende Bewegungen umwandeln und umgekehrt. Wie alle Koppelgetriebe zeichnet sie sich durch die Kopplung von mindestens zwei der beweglichen Elemente mit einer Koppel aus. Meist wird eine Kurbel als Antrieb und eine Schwinge als Abtrieb verwendet, jedoch ist auch der umgekehrte Fall möglich (s. dazu Holländer).

Kurbel-Schwinge-Ausführungen werden unter anderem in der Automatisierung und Teilautomatisierung eingesetzt, beispielsweise bei der Erzeugung eines diskontinuierlichen Vortriebs von Material. Geläufig (und gelegentlich gesehen) in Sägewerken zum Vorschieben der Holzstämme bzw. Bretter, beim Werkzeugantrieb von Stoßmaschinen zur spanenden Werkstoffbearbeitung oder beim Scheibenwischer eines Kraftfahrzeugs (siehe Schema-Zeichnungen).

Schwinge-Kurbel-Ausführungen werden oftmals in handbetriebenen Geräte benutzt, wie z. B. in Pumpen oder Draisinen.

Siehe auch: Koppelgetriebe

Funktionsvoraussetzungen

Die Kurbel ist nur dann voll drehbar (d. h. umlauffähig), wenn die Längen der Teile der Kurbelschwinge in einem bestimmten Verhältnis zueinander stehen.

Der deutsche Ingenieur Franz Grashof hat dazu einen Lehrsatz formuliert: Die Kurbel als kleinstes Glied einer Kurbelschwinge (Viergelenkkette) ist voll drehfähig, wenn die Kurbel zusammen mit dem längsten Glied der Kurbelschwinge kleiner ist als die anderen beiden Glieder.

Grundsätzlich sind hier zwei Fälle zu unterscheiden, zwei Ungleichungen müssen von der Kurbelschwinge erfüllt werden:

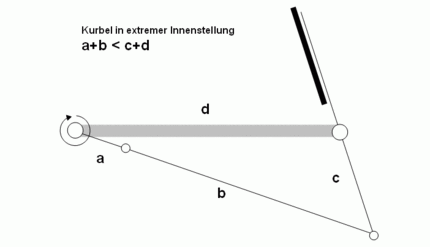
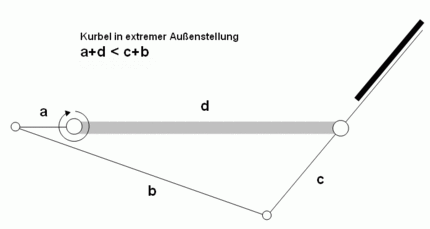
Aus diesen beiden Ungleichungen folgt auch, dass a auf jeden Fall kleiner c sein muss und zwar genau um den zweifachen Unterschied zwischen b und d.

Sind a+b = c+d und/oder a+d = c+b, so gerät die Schwinge bei mindestens einer der beiden extremen Kurbelstellungen in Totpunktlage. Dabei besteht die Gefahr, dass die Schwinge in die Gegenrichtung umschlägt. Müsste die Kurbelschwinge in dieser Stellung wieder neu anlaufen, würden ebenfalls Probleme auftreten.

Weitere Darstellung:

Weblinks

• [1] Simulation von Kurbelschwingen, Daten können selber eingegeben werden.