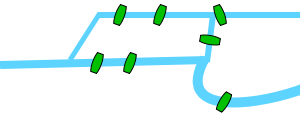
Königsberger Brückenproblem

Das Königsberger Brückenproblem

Schematische Darstellung

Darstellung als Graph

Das Königsberger Brückenproblem ist eine mathematische Fragestellung des frühen 18. Jahrhunderts, die anhand von sieben Brücken der Stadt Königsberg illustriert wurde. Das Problem bestand darin, zu klären, ob es einen Weg gibt, bei dem man alle sieben Brücken über den Pregel genau einmal überquert, und wenn ja, ob auch ein Rundweg möglich ist, bei dem man wieder zum Ausgangspunkt gelangt. Wie Leonhard Euler 1736 bewies, war ein solcher Weg bzw. „Eulerscher Weg“ in Königsberg nicht möglich, da zu allen vier Ufergebieten bzw. Inseln eine ungerade Zahl von Brücken führte. Es dürfte maximal zwei Ufer (Knoten) mit einer ungeraden Zahl von angeschlossenen Brücken (Kanten) geben. Diese zwei Ufer könnten Ausgangs- bzw. Endpunkt sein. Die restlichen Ufer müssten eine gerade Anzahl von Brücken haben, um sie auch wieder verlassen zu können.

Das Brückenproblem ist kein klassisches geometrisches Problem, da es nicht auf die präzise Lage der Brücken ankommt, sondern nur darauf, welche Brücke welche Inseln miteinander verbindet. Es handelt sich deshalb um ein topologisches Problem, das Euler mit Methoden löste, die heute der Graphentheorie zugerechnet werden. Das Problem lässt sich auf beliebige Graphen verallgemeinern, und auf die Frage, ob es darin einen Zyklus gibt, der alle Kanten genau einmal benutzt. Ein solcher Zyklus wird als Eulerkreis bezeichnet und ein Graph, der einen Eulerkreis besitzt, als eulersch. Die Frage, ob ein Graph eulersch ist, lässt sich relativ einfach beantworten und ist auch in gerichteten Graphen und Graphen mit Mehrfachkanten möglich.

Durch Kriegseinwirkung und Umbauten nach 1945 ist die ursprüngliche Situation im heutigen Kaliningrad nicht mehr gegeben. Zwei der zur Insel Kneiphof führenden Brücken existieren nicht mehr, am nördlichen und südlichen Ufer enden nur noch jeweils zwei anstatt drei Brücken. Nun ist zwar ein Eulerweg möglich, jedoch noch immer kein Eulerkreis.

Die sieben Brücken mit Namen

1. Grüne Brücke
2. Krämerbrücke
3. Schmiedebrücke
4. Köttelbrücke
5. Honigbrücke
6. Holzbrücke
7. Hohe Brücke

Siehe auch: Königsberger Brücken

Literatur

• Gustav Theodor Hoffheinz: Die sieben Brücken in Königsberg. Altpreußische Monatsschrift, N. F. 18 (1881), S. 282 ff.
• Wladimir Velminski: Leonhard Euler. Die Geburt der Graphentheorie. Kulturverlag Kadmos, Berlin 2008, ISBN 978-3-86599-056-3.

Weblinks

• Königsberg bridges. In: MacTutor History of Mathematics archive (englisch)
• Das Königsberger Brückenproblem – Didaktisch gelungene Bearbeitung bei MathePrisma.
• Spaziergänge und Buslinien – knappere anschauliche und theoretische Darstellung mit Hilfe von Kantenzügen von Franz Embacher, Uni Wien.