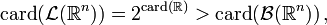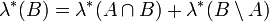Lebesguemaß

Das Lebesgue-Maß [ləˈbɛg] (nach Henri Léon Lebesgue) ist das Maß im euklidischen Raum, das geometrischen Objekten ihren Inhalt (Länge, Flächeninhalt, Volumen, …) zuordnet.

Das Lebesgue-Maß ist aus der Sicht der modernen Mathematik der natürliche Begriff für Volumen und Flächeninhalt. Dieses Konzept ist das Endprodukt einer ganzen Reihe von Ideen, die versuchten, den Begriff Volumen mathematisch exakt zu fassen. Erst mit dem Lebesgue-Maß kann dieser Prozess als abgeschlossen gelten. Das Lebesgue-Maß ordnet nicht nur einfachen geometrischen Objekten, sondern auch viel allgemeineren Mengen, einschließlich aller offenen und abgeschlossenen Mengen, einen Inhalt zu. Die Existenz von nicht Lebesgue-messbaren Mengen lässt sich nur mit dem Auswahlaxiom zeigen.^[1][2][3]

Das Borel-Lebesgue-Maß auf der Borel-σ-Algebra 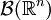$\mathcal B(\R^n)$ (auch als Lebesgue-Borel-Maß oder nur Borel-Maß bezeichnet) ist das eindeutige Maß λ mit der Eigenschaft

$\lambda([a_1, b_1]\times\cdots\times[a_n, b_n]) \, = \, (b_1-a_1)\,\cdot\,\cdots\,\cdot\,(b_n-a_n)$,

d. h. das Maß, das Intervallen ihre Länge zuordnet (im 1-dimensionalen), Rechtecken ihren Flächeninhalt zuordnet (im 2-dimensionalen), Quadern ihr Volumen zuordnet (im 3-dimensionalen), etc. Durch diese Bedingung wird der Inhalt λ(B) beliebiger Borel-Mengen eindeutig festgelegt. Die Borel-Mengen werden auch Borel-messbar oder B-messbar genannt. Das Borel-Maß ist bewegungsinvariant und normiert, aber nicht vollständig. Die Existenz des Borel-Lebesgue-Maß wurde im eindimensionalen zum ersten Mal von Émile Borel 1895 bewiesen, eine modernere Konstruktion über sogenannte äußere Maße geht auf Constantin Carathéodory (1918) zurück.^[4]

Das Lebesgue-Maß ist das vollständige Maß λ, das man aus diesem Maß erhält, wenn man zu 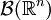$\mathcal B(\R^n)$ alle Mengen A hinzufügt, die zwischen zwei Borel-Mengen liegen (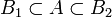$B_1 \subset A \subset B_2$), welche denselben Inhalt haben, genauer 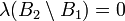$\lambda(B_2 \setminus B_1) = 0$, und so λ(A) festlegen. Die Mengen, für die das Lebesgue-Maß auf diese Weise definiert ist, heißen Lebesgue-messbar (oder L-messbar).

Die Einführung des Lebesgue-Maßes stellt keine triviale Vervollständigung dar – es lässt sich nämlich zeigen, dass die Menge der L-messbaren Mengen 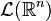$\mathcal L(\R^n)$ wesentlich größer als die Menge der B-messbaren Mengen ist:^[5][6]

$\operatorname{card}(\mathcal L(\R^n))= 2^{\operatorname{card}(\mathbb{R})}>\operatorname{card}(\mathcal B(\R^n))\,,$

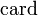wobei $\operatorname{card}$ die übliche Abkürzung für die Kardinalität einer Menge bedeuten soll.

Mengen, deren Lebesgue-Maß gleich 0 ist, werden Lebesgue-Nullmengen genannt. Abzählbare Punktmengen wie z. B. die Menge der rationalen Zahlen sind immer Lebesgue-Nullmengen. Ein Beispiel für eine überabzählbare Lebesgue-Nullmenge ist das Cantorsche Diskontinuum.^[7] Gilt eine mathematische Aussage für ein Gebiet mit Ausnahme einer Lebesgue-Nullmenge innerhalb des Gebietes, so sagt man: Die Aussage gilt Lebesgue-fast-überall.

Das Lebesgue-Maß ist das Haar-Maß auf der topologischen Gruppe $\R^n$.

Konstruktion des Lebesgue-Maßes

Eine mögliche Definition des Lebesgue-Maßes ist die Konstruktion von Carathéodory. Für eine gegebene Menge A definiert man

$\lambda^*(A) := \inf \left\{\sum_{i \geq 1} \operatorname{vol}(A_i): A \subseteq \bigcup_{i \geq 1} A_i,\ A_i \in \mathcal{D}\right\}$.

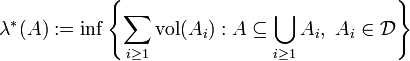Hier ist 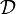$\mathcal{D}$ die Menge der dyadischen Elementarzellen und 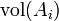$\operatorname{vol}(A_i)$ das Volumen von A_i. Da dies nur aus Produkten von Intervallen besteht, lässt sich das Volumen einfach als Produkt der einzelnen Seitenlängen berechnen.

λ ^* ist ein metrisches äußeres Maß und auf der gesamten Potenzmenge 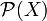$\mathcal{P}(X)$ der zugrunde liegenden Menge X definiert. λ ^* ist in der Regel kein Maß. Um zu einem Maß zu kommen, muss man wie folgt von der Potenzmenge zu einem kleineren Mengensystem übergehen.

Eine Menge 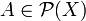$A \in \mathcal{P}(X)$ ist λ ^* -messbar wenn 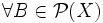$\forall B \in \mathcal{P}(X)$ gilt:

$\lambda^*(B) = \lambda^*(A\cap B) + \lambda^*(B \setminus A)$

(siehe Messbarkeit nach Carathéodory).

Alle bezüglich λ ^* messbaren Mengen aus 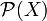$\mathcal{P}(X)$ bilden eine σ-Algebra 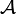$\mathcal{A}$ und λ ^* darauf ein Maß, d.h., 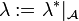$\lambda := \lambda^*\vert_\mathcal{A}$ ist ein Maß.

Siehe auch

• Lebesgue-Integral
• Lp-Raum

Quellen und Bemerkungen

1. ↑ Nicht messbar sind z. B. die sogenannten Vitali-Mengen, die aus je einem Vertreter jeder Restklasse modulo $\mathbb{Q}$ (Ideal der rationalen Zahlen) in $\mathbb{R}$ (Ring der reellen Zahlen) bestehen.
2. ↑ Ein Paradoxon, das auf nicht Lebesgue-messbaren Mengen beruht, ist das Banach-Tarski-Paradoxon.
3. ↑ siehe P. Komjath, V. Totik: Problems and Theorems in Classical Set Theory. 28., Springer, 2006, ISBN 0-387-30293-X, sowie A. Kanamori: The Higher Infinite. Springer, 1994, ISBN 0-387-57071-3, Ch. 3., §11. (mit Beweis)
4. ↑ Olav Kallenberg: Foundations of Modern Probability. Springer, New York 2002, ISBN 0387953132, S. 570.
5. ↑ M. Leinert: Integration und Maß. Vieweg, 1995, ISBN 3-528-06385-8, (4.20)
6. ↑ Beispiele für nicht B-messbare L-messbare Mengen sind zum ersten Mal von Suslin gegeben worden. Er hat dabei das System der sogenannten analytischen Mengen entwickelt, das eine echte Erweiterung des Systems der Borelschen Mengen ist und komplett im System der L-messbaren Mengen liegt.
7. ↑ Das cantorsche Diskontinuum ist auch eine borelsche Nullmenge. Da das Lebesgue-Maß vollständig ist, sind alle Untermengen des cantorschen Diskontinuums L-messbar. Daraus folgt die erste von den oben erwähnten Ungleichungen – nämlich, dass das System der L-messbaren Mengen echt mächtiger als das Kontinuum ist.