Leerstring

Das leere Wort ist in der Theoretischen Informatik und in der Praktischen Informatik ein Wort, das aus keinem einzigen Zeichen besteht, also eine Zeichenkette der Länge 0 (auch Leerstring genannt). In vielen Programmiersprachen wird ein solcher String durch ein Literal dargestellt, bei dem die beiden Anfangs- und Endzeichen, die eine Zeichenkette einschließen, unmittelbar aufeinander folgen, z. B. "" in Perl oder Java.

Definition

Das leere Wort über dem Alphabet Σ ist eine Folge von Elementen aus Σ der Länge 0.

Schreibweise

Das leere Wort wird meist mit dem griechischen Buchstaben $\varepsilon$ (Epsilon für Englisch „empty“) dargestellt, oft findet sich dafür aber auch der griechische Buchstabe λ (Lambda, vom Deutschen „leer“). Andere übliche Darstellungen sind ε, e (ebenfalls für „empty“) und 1 (als Einselement eines multiplikativ geschriebenen Monoids).

Merkmale

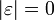• $|\varepsilon| = 0$ Die Länge des leeren Wortes ist stets 0. Diese Eigenschaft folgt direkt aus der Definition.

• $\forall w \in \Sigma^*: \varepsilon w = w \varepsilon = w$ Das leere Wort bildet bei der Konkatenation von Wörtern das neutrale Element, sprich, die Verkettung eines beliebigen Wortes w über ein beliebiges Alphabet Σ mit $\varepsilon$ ergibt stets wieder w.

• $\varepsilon \notin \Sigma$ Das leere Wort $\varepsilon$ ist niemals Element eines Alphabets Σ. Das würde der Definition widersprechen, die $\varepsilon$ gerade als das Fehlen jeglicher Symbole aus Σ definiert.

• $\varepsilon \in \Sigma^*$ Das leere Wort $\varepsilon$ ist Element der Kleeneschen Hülle über jedes beliebige Alphabet Σ.

• $\varepsilon^R = \varepsilon$ Das leere Wort ist identisch mit seiner Spiegelung und damit ein Palindrom.

Spezielle Merkmale bei speziellen Anwendungen

• $[\varepsilon] = L$ Betrachtet man die Äquivalenzklassen einer formalen Sprache L bezüglich der Nerode-Relation ~, so bildet $\varepsilon$ stets eine Äquivalenzklasse, die exakt L entspricht. Demnach beträgt der Index von L bezüglich ~ stets mindestens 1, in Zeichen ind(L) > = 1. Daraus wiederum lässt sich folgern, dass ein Deterministischer endlicher Automat, der L akzeptiert, aus mindestens einem Zustand bestehen muss.

• $\varepsilon$-Übergänge in Nichtdeterministischen endlichen Automaten sind Argumentpaare (q,a) der Übergangsfunktion δ mit $q \in \Sigma$ und $a = \varepsilon$. Ein solcher Übergang δ(q₁,δ) = q₂ bedeutet, dass der Automat seinen Zustand von q₁ nach q₂ ändern kann, ohne dass ein Zeichen eingegeben wird. $\varepsilon$-Übergänge sind damit die Grundlage des Nichtdeterminismus. Sie werden im Graphen als Kanten kenntlich gemacht, die mit einem $\varepsilon$ beschriftet sind.