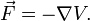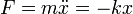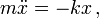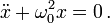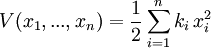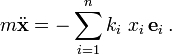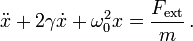- Harmonische Schwingung
-
Ein harmonischer Oszillator ist ein physikalisches System, bei dem die Zeitentwicklung eines der Systemparameter einer Sinusfunktion folgen, also "harmonisch schwingen" kann. Beispiele für harmonische Oszillatoren sind das Fadenpendel oder der Schwingkreis. Der Systemparameter, der harmonisch schwingen kann, genügt dabei immer der Differentialgleichung
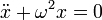 .
.Inhaltsverzeichnis
Allgemeines
Als harmonischen Oszillator bezeichnet man in der klassischen Mechanik eine Punktmasse, die einem Kraftfeld
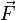 ausgesetzt ist, das durch folgende Bedingungen charakterisiert ist:
ausgesetzt ist, das durch folgende Bedingungen charakterisiert ist:- In jedem Raumpunkt zeigt die Kraft
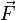 in Richtung eines fest gewählten Punktes, dem sogenannten Ruhepunkt oder auch der Ruhelage des Systems.
in Richtung eines fest gewählten Punktes, dem sogenannten Ruhepunkt oder auch der Ruhelage des Systems. - Lenkt man das Teilchen aus der Ruhelage in eine bestimmte Richtung aus, so ist die Kraft, die auf das Teilchen wirkt, der Auslenkung proportional. Insbesondere erfährt ein in der Ruhelage liegendes Teilchen keinerlei Kraft, woraus sich auch der Name "Ruhelage" ableitet. Die Namensgebung ist allerdings in dieser Hinsicht etwas irreführend: Zwar wirkt auf ein Teilchen in der Ruhelage keine Kraft, das Teilchen muss sich dort allerdings keinesfalls in Ruhe befinden; i.A. nimmt es dort sogar seine Maximalgeschwindigkeit an.
- Hängt die Stärke der Kraft nur von dem Betrag der Auslenkung - also der Entfernung des Teilchens von der Ruhelage, nicht aber von der Richtung der Auslenkung ab, so nennt man den Oszillator isotrop, andernfalls anisotrop. Da es in einer Dimension nur eine Richtung gibt, sind alle eindimensionalen harmonischen Oszillatoren isotrop.
Bewegt man das Teilchen aus der Ruhelage zu irgendeinem anderen Punkt im Raum, so zieht das Kraftfeld das Teilchen stets wieder in Richtung der Ruhelage an. Daher nennt man die Kraft, die das Teilchen erfährt, auch Rückstell- oder Rückholkraft. Der Name Oszillator rührt von der Tatsache her, dass ein Teilchen in einem so beschaffenen Kraftfeld - das man auch als Oszillatorkraftfeld bezeichnet - (harmonische) Schwingungen ausführt. Der harmonische Oszillator ist eines der wichtigsten Modelle der Mechanik, vielleicht sogar der Physik überhaupt.
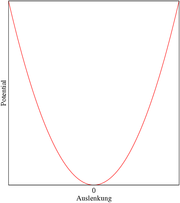
Potenzialverlauf
Man kann allgemein zeigen, dass das Kraftfeld eines harmonischen Oszillators konservativ ist. Es existiert daher für jedes Oszillator-Kraftfeld ein Potenzial, also ein Skalarfeld V mit
Die grafische Darstellung des Potenzials eines Oszillatorkraftfeldes hat die Form einer quadratischen Parabel. Besondere Bedeutung gewinnt das Potenzial des harmonischen Oszillators in der Quantenmechanik, da die für die Quantenmechanik fundamentale Schrödinger-Gleichung nur Potenziale, keine Kräfte enthält. Den harmonischen Oszillator der Quantenmechanik behandelt der Artikel Harmonischer Oszillator (Quantenmechanik).
Realisierbarkeit
Ein idealer harmonischer Oszillator, bei dem die Rückstellkraft für beliebig große Auslenkungen linear mit der Auslenkung ansteigt, existiert in der Natur nicht. Dennoch ist das Konzept für die Physik von fundamentaler Bedeutung, da oft nur kleine Auslenkungen eines Objekts aus der Ruhelage betrachtet werden. Beschränkt man sich darauf, so können viele Kraftfelder in guter Näherung durch ein Oszillatorkraftfeld ersetzt und das gesamte Problem als harmonischer Oszillator beschrieben werden. Der Vorteil einer solchen Näherung (die man auch harmonische Näherung nennt) besteht darin, dass das Problem mit Standardmethoden der theoretischen Physik handhabbar wird und einfach zu interpretierende, analytische Lösungen liefert.
Ihre mathematische Begründung findet die harmonische Näherung in der Tatsache, dass die Potenziale vieler Kraftfelder um einen bestimmten, fest gewählten Punkt taylor-entwickelbar sind, was man am besten am Beispiel eines Kraftfeldes in einer Dimension verdeutlicht: ist zu irgendeinem Kraftfeld das Potenzial V gegeben und ist dieses hinreichend oft differenzierbar, so gilt nach dem Satz von Taylor:
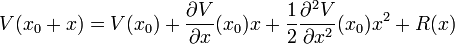
wobei R(x), das sogenannte Restglied, für kleine Auslenkungen x, also für
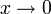 , verschwindet. Für kleine Auslenkungen gilt daher:
, verschwindet. Für kleine Auslenkungen gilt daher: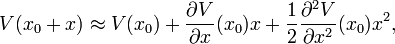
wählt man als Entwicklungspunkt x0 einen Extremalpunkt des Potenzials, so ist
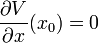 , setzt man weiterhin V(x0) = 0 (was stets möglich ist), so erhält man:
, setzt man weiterhin V(x0) = 0 (was stets möglich ist), so erhält man: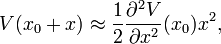
was dem Potenzial eines harmonischen Oszillators entspricht.
Das heißt, bei kleiner Auslenkung verhält sich auch ein System mit anharmonischem Potenzial wie ein harmonischer Oszillator. Beispiele für solche Oszillatoren sind das Fadenpendel, Federpendel, Schwingquarze oder Stimmgabeln.
Der harmonische Oszillator in verschiedenen Dimensionen
Oszillator in einer Dimension
Wählt man den Nullpunkt als Ruhelage, ist die Kraft, die auf einen eindimensionalen harmonischen Oszillator wirkt, durch
gegeben, wobei k die Federkonstante des Oszillators ist. Der Name Federkonstante rührt von dem Standardbeispiel eines solchen Systems her: Einer an einer Spiralfeder befestige Masse. Für kleine Auslenkungen ist die Kraft, die auf diese Masse wirkt, annähernd proportional zur Auslenkung von der Ruhelage. Die Ruhelage des Massepunktes ist dabei durch eine vollkommen entspannte, als weder gedehnte noch gestreckte Feder charakterisiert. Die newtonsche Bewegungsgleichung des harmonischen Oszillators lautet dann:
sie wird üblicherweise umgeschrieben zu
Die Lösung dieser Differentialgleichung ist eine harmonische Schwingung
- x(t) = u1cos(ω0t) + u2sin(ω0t)
mit Kreisfrequenz
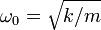 . Die Amplituden u1 und u2 hängen dabei von den Anfangsbedingungen ab.
. Die Amplituden u1 und u2 hängen dabei von den Anfangsbedingungen ab.Der Oszillator in mehreren Dimensionen
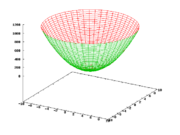
Ein harmonischer Oszillator in n Dimensionen hat das Potential
und das Kraftgesetz
Da die Kraftkomponenete in einer Dimension nur von der Auslenkung in dieser Dimension abhängt, sind die Lösungen für die einzelnen Komponenten des Ortsvektors die Lösungen des entsprechenden eindimensionalen Problems.
Verallgemeinerungen des harmonischen Oszillators
Oszillator mit Reibung
Eine mechanische Schwingung ist im allgemeinen nicht reibungsfrei. Das heißt, die Schwingung verliert Energie durch Reibung. In der Differentialgleichung tritt dann zur beschleunigenden Kraft F eine Reibungskraft FR hinzu:
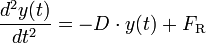 .
.
Der genaue Ausdruck für FR hängt von der Art der Reibung ab. Im Falle von Gleitreibung ist der Betrag von FR konstant und das Vorzeichen ist der Geschwindigkeit entgegengesetzt.
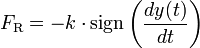 .
.
Bei kleinen Reynoldszahlen wird die Luftreibung durch das Gesetz von Stokes bestimmt. Das heißt, die Reibungskraft ist proportional zur Geschwindigkeit, also zur ersten zeitlichen Ableitung der Auslenkung:
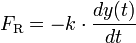 .
.
Die Lösungen der um diese Reibungskräfte ergänzten Differentialgleichung bestehen in Schwingungen mit linear bzw. exponentiell abnehmender Amplitude.
Oszillator mit Dämpfung und Anregung
Zur Verallgemeinerung kann der Rückstellkraft noch ein Dämpfungsterm
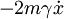 , welcher zur Geschwindigkeit
, welcher zur Geschwindigkeit 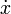 proportional und entgegengesetzt ausgerichtet ist, sowie eine antreibende Kraft Fext hinzugefügt werden. Dann ergibt sich die Differentialgleichung eines angetriebenen, gedämpften harmonischen Oszillators in einer Dimension zu
proportional und entgegengesetzt ausgerichtet ist, sowie eine antreibende Kraft Fext hinzugefügt werden. Dann ergibt sich die Differentialgleichung eines angetriebenen, gedämpften harmonischen Oszillators in einer Dimension zuWenn die von außen auf das System einwirkende Kraft ebenfalls periodisch ist, also in Schwingungen übertragen wird, so kann sie dem Oszillator Energie hinzufügen oder entziehen, je nach Phasenlage. Mit jedem Kraftübertrag wird dann etwas Energie zur Schwingung hinzugefügt oder entfernt, so dass die Amplitude anwächst oder abnimmt. Bei einem schwach gedämpften System kann dies zur sogenannten Resonanzkatastrophe führen, einem extremen Anstieg der Amplitude, welcher das System zerstören kann.
Schwingungen im Allgemeinen
Viele Probleme der Physik führen auf Differenzialgleichungen, die zu der Gleichung eines (gedämpften) harmonischen Oszillators formgleich sind. Ein typisches Beispiel ist der Verlauf von Strömen und Spannung in einem Schwingkreis. Es ist allgemein üblich, Probleme dieser Art ebenfalls als harmonischen Oszillator zu bezeichnen, auch wenn diese weitgehend nicht mechanischer Natur sind, vgl. auch den Artikel Oszillator.
Anharmonischer Oszillator
Beim anharmonischen Oszillator treten mehr oder minder große Abweichungen vom linearen Kraftgesetz bzw. vom quadratischen Potential auf. Ist das System stark gedämpft und die Anharmonizität klein, so macht sie sich in der Regel nur dadurch bemerkbar, dass Oberschwingungen der Grundfrequenz auftreten. Wenn das System nur schwach gedämpft ist oder der nichtlineare Term das Kraftgesetz dominiert, so kann chaotisches Verhalten auftreten. Beispiele dafür sind der Toda-Oszillator und der Duffing-Oszillator.
Siehe auch
Weblinks
- In jedem Raumpunkt zeigt die Kraft
Wikimedia Foundation.