Amplitude

Die Amplitude ist die maximale Auslenkung einer sinusförmigen Wechselgröße. Im physikalischen Kontext wird der Zusammenhang durch physikalische Größen wie beispielsweise eine Wechselspannung und deren Verlauf über der Zeit oder über dem Ort ausgedrückt. Die Amplitude tritt dann als maximale Auslenkung von Schwingungen oder Wellen aus der Lage des arithmetischen Mittelwertes auf.

Sinusförmige Wechselspannung:
1 = Amplitude,
2 = Spitze-Spitze-Wert,
3 = Effektivwert,
4 = Periodendauer

In DIN 40110-1 („Wechselstromgrößen") wird unterschieden zwischen

• Scheitelwert û einer periodischen Wechselspannung und
• Amplitude û einer sinusförmigen Wechselspannung.

Für weitere Benennungen, die nicht auf Wechselgrößen beschränkt sind, aber allgemein für periodische Vorgänge verwendet werden, z. B. bei Mischspannung, siehe unter Scheitelwert.

Der Abstand zwischen Maximum und Minimum wird in derselben Norm bei Schwingungen als Schwingungsbreite oder auch als Spitze-Tal-Wert bezeichnet (früher als Spitze-Spitze-Wert).

Mathematische Darstellung

Eine ungedämpfte sinusförmige oder harmonische Schwingung wird durch

$y(t)=\hat y \cos(\omega t + \varphi)$

mit der Amplitude $\hat y\;$, Kreisfrequenz ω und Nullphasenwinkel φ beschrieben. Die Amplitude ist zeitunabhängig und damit konstant.
Eine andere Möglichkeit der Beschreibung ist die komplexe Darstellung mittels der Eulerschen Formel (mit der in der Elektrotechnik üblichen imaginären Einheit j (DIN 1302)).

$\underline y(t)=\hat y \;e^{\mathrm j(\omega t + \varphi)}=\hat y \;e^{\mathrm j \varphi} e^{\mathrm j \omega t}$

Dabei hat nur der Realteil physikalische Bedeutung. Diese Form erleichtert aber viele Berechnungen, siehe Komplexe Wechselstromrechnung. Der Ausdruck

$\underline{\hat y} = \hat y \;e^{\mathrm j \varphi}$

ist die komplexe Amplitude, deren Betrag gleich der Amplitude $\hat y\;$ und deren Argument (Winkel) gleich φ ist.

In bestimmten Zusammenhängen kann sich die Amplitude auch langsam gegenüber der zugehörigen Schwingung ändern, z. B. bei Dämpfung oder Modulation.

Eine gedämpfte, nicht periodische Schwingung wird in DIN 5483-1 („Zeitabhängige Größen“) mit dem Abklingkoeffizienten δ durch

$y(t)=\hat y \;e^{-\delta t} \cos(\omega t+\varphi)$

oder in komplexer Form

$\underline y(t)=\underline{\hat y} \;e^{-\delta t} e^{\mathrm j \omega t}$

beschrieben. Der Ausdruck

$\underline A(t)= \underline{\hat y}\; e^{-\delta t}$

ist die zeitveränderliche (komplexe) Amplitudenfunktion.

Amplitude einer harmonischen Pendelschwingung

Beispiele

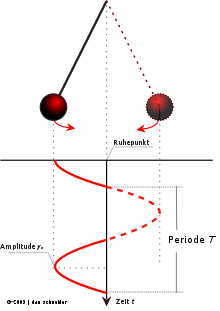
Ein Pendel schwingt von rechts nach links und zurück. Die Distanz zwischen folgenden beiden Punkten ist die Amplitude der Schwingung:

• der Punkt der Pendelbewegung, in der das Pendel die größte Auslenkung hat und seine Bewegungsrichtung umkehrt,
• der Punkt, in dem das Pendel hängt, wenn es in Ruhe ist (Bezugspunkt).

Eine gezielte Beeinflussung der Amplitude findet bei der Amplitudenmodulation statt.

Literaturquellen

• I. Bronstein, K. Semendjaev, G. Musiol, H. Mühlig: Taschenbuch der Mathematik. 5. Auflage. Harri Deutsch, Dresden 2001, ISBN 3-8171-2005-2.

Siehe auch

• Scheitelwert
• Amplitudenspektrum

Weblinks

 Wiktionary: Amplitude – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen