Ljapunow-Fraktal

Ljapunow-Fraktal mit der Sequenz ab

Ljapunow-Fraktal mit der Sequenz AAAABBB

In der Mathematik sind Ljapunow-Diagramme (auch bekannt als Ljapunow-Fraktale oder Markus-Ljapunow-Fraktale; nach Alexander Michailowitsch Ljapunow) Fraktale hergeleitet von einer Erweiterung der logistischen Gleichung, in der der Wachstumsgrad der Population, r, periodisch zwischen zwei Werten a und b schwankt.

Die logistische Gleichung lautet:

x_{n + 1} = r_nx_n(1 − x_n)

Mit einem Startwert, der üblicherweise bei x₀ = 0,5 gewählt wird.

Dabei wird r_n = a oder r_n = b für die n-te Iteration der logistischen Gleichung gewählt, je nach dem Wert an der Stelle n in einer unendlichen Folge, die aus der Hintereinanderreihung von einfachen Mustern (Sequenzen) von Symbolen (a,b) gebildet wird, z. B. mit dem Muster (aababab). 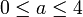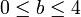Dann werden für Werte (a,b) aus Intervallen, die – um interessante Figuren zu bekommen – meist im Bereich $0 \le a \le 4$ und $0 \le b \le 4$ gewählt werden, jeweils die Iterationswerte der logistischen Gleichung berechnet und der Ljapunow-Exponent berechnet:

$\lambda = \lim_{N \rightarrow \infty} {1 \over N} \sum_{n = 1}^N \log \left|{dx_{n+1} \over dx_n}\right| = \lim_{N \rightarrow \infty} {1 \over N} \sum_{n = 1}^N \log |r_n (1 - 2x_n)|$

Ist der Wert von λ < 0, wählt man für den Punkt mit den Koordinaten (a,b) z. B. gelb als Farbe, ist er größer als Null (was zu exponentiellem Wachstum führt, Chaos), wählt man z. B. blau aus Farbe. Entsprechend kann man die Farbwerte noch abstufen je nach der Größe von λ. Das Ergebnis ist das Ljapunow-Diagramm, die häufig fraktaler Natur sind. 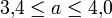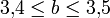Ein Beispiel ist das Diagramm Zirkon Zity, gebildet mit $3{,}4 \le a \le 4{,}0$ und $3{,}4 \le b \le 3{,}5$ und der Sequenz (bbbbbbaaaaaa).

Quellen

Mario Markus: Ljapunow-Diagramme. Spektrum der Wissenschaft 1995/4, 66–73.

Weblinks

• EFGs, Fraktale und Chaos – Ljapunow-Exponenten (englisch)
• Lyapunov Space – Das Chaos Hypertextbuch von Glenn Elert (englisch)
• Ljapunow-Diagramme im Design