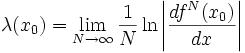- Ljapunow-Exponenten
-
Der Ljapunow-Exponent eines dynamischen Systems (nach Alexander Michailowitsch Ljapunow) beschreibt die Geschwindigkeit, mit der sich zwei (nahe beieinanderliegende) Punkte im Phasenraum voneinander entfernen oder annähern (je nach Vorzeichen). Pro Dimension des Phasenraums gibt es einen Ljapunow-Exponenten, die zusammen das sogenannte Ljapunow-Spektrum bilden. Häufig betrachtet man allerdings nur den größten Ljapunow-Exponenten, da dieser das gesamte Systemverhalten bestimmt.
Im Eindimensionalen ist der Ljapunow-Exponent λ einer iterierten Abbildung xn + 1 = f(xn) wie folgt definiert:
Inhaltsverzeichnis
Eigenschaften
- Ist der größte Ljapunow-Exponent positiv, so ist das System in der Regel divergent
- Ist er negativ, so entspricht dies einer Phasenraumkontraktion, d.h. das System ist dissipativ und agiert stationär oder periodisch stabil.
- Ist die Summe der Ljapunow-Exponenten Null, so handelt es sich um ein konservatives System
Bedeutung der Ljapunow-Exponenten
Kaplan-Yorke-Vermutung
Die Kaplan-Yorke-Vermutung liefert eine Abschätzung für die obere Grenze der Informationsdimension D1 mit Hilfe des Ljapunow-Spektrums ab. Diese so genannte Kaplan-Yorke-Dimension DKY ist wie folgt definiert:
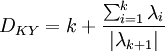 ,
,
wobei k die größte natürliche Zahl ist, für die die Summe positiv bleibt
Ljapunow-Zeit
Das Inverse des größten Ljapunow-Exponenten, die sogenannte Ljapunow-Zeit bzw. die mittlere Prediktionszeit, ist die Zeit, für die sich sinnvolle Vorhersagen über das Systemverhalten machen lassen.
Weblinks
Quellen
- Kantz, H. und Schreiber, T.: Nonlinear Time Series Analysis. Cambridge University Press, Cambridge 2004, ISBN 0-521-52902-6
Wikimedia Foundation.