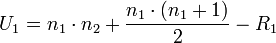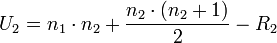Mann-Whitney

Der Mann-Whitney-Test ("Mann-Whitney-U-Test" oder kurz "U-Test") ist ein parameterfreier statistischer Test. Der U-Test ist ein Homogenitätstest. Er dient zur Überprüfung der Signifikanz der Übereinstimmung zweier Verteilungen, also ob zwei unabhängige Verteilungen A und B (zum Beispiel eine unbeeinflusste und eine beeinflusste) zu derselben Grundgesamtheit gehören.

Der Test wurde von Henry Mann und Donald Whitney (1947) sowie Frank Wilcoxon (1945) entwickelt und wird deshalb auch Mann-Whitney-Wilcoxon (MWW)-Test oder Wilcoxon-Rangsummentest genannt.

Man hat 2 Stichproben vor sich, Stichprobe A mit n₁ Werten und Stichprobe B mit n₂ Werten. Man vergleicht jeden Wert der Stichprobe A mit jedem Wert der Stichprobe B. Es gibt also 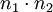$n_1 \cdot n_2$ Vergleiche. Die Nullhypothese H(0) besagt, dass es keinen Unterschied zwischen den Verteilungen gibt, d. h. A = B.

Der Test funktioniert einseitig oder zweiseitig. Beim einseitigen Test wird geprüft, ob A > B bzw. A < B ist, beim zweiseitigen Test wird geprüft, ob A = B ist.

Zunächst wird aus beiden Zahlenreihen je eine Prüfgröße U gebildet:

$U_1=n_1 \cdot n_2 +{n_1 \cdot (n_1+1) \over 2}-R_1$

$U_2=n_1 \cdot n_2 +{n_2 \cdot (n_2+1) \over 2}-R_2$

n₁ und n₂ sind dabei die Anzahlen der Zahlenwerte pro Reihe, R₁ und R₂ sind die Rangzahlen der geordneten Reihen. Um diese zu ermitteln, werden alle Werte beider Reihen zusammen aufsteigend in eine Tabelle geschrieben. Die Rangzahlen der Zahlenwerte werden für A und für B getrennt in zwei Spalten aufsummiert. Sind zwei oder mehrere Werte in beiden Datensätzen gleich, dann müssen in beiden Rangspalten jeweils die Mediane (bzw. arithmetischen Mittel) eingetragen werden. Für den zweiseitigen Test benötigt man das Minimum von U1 und U2, also min(U) = min(U1,U2).

U1 und U2 bzw. min(U) werden nun mit der Testgröße U() verglichen. Beim einseitigen Test ist diese Testgröße

$U = \frac{n_1 \cdot n_2}{2} - \mathrm{u}(\alpha) \cdot \sqrt{n_1 \cdot n_2 \cdot (n_1+n_2+1) \over 12}$.

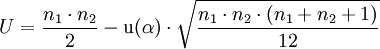und beim zweiseitigen Test:

$U = \frac{n_1 \cdot n_2}{2} - \mathrm{u}\left(\frac{\alpha}{2}\right) \cdot \sqrt{n_1 \cdot n_2 \cdot (n_1+n_2+1) \over 12}$.

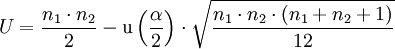U hängt von n₁ und n₂ ab, außerdem über den Parametern u(α) bzw. 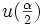$u(\tfrac{\alpha}{2})$ (oder λ(1 − α) bzw. 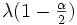$\lambda(1-\tfrac{\alpha}{2})$, wobei λ_q das Quantil der Standard-Normalverteilung bezeichnet) vom Signifikanzniveau α. In Abhängigkeit vom gewünschten Signifikanzniveau (zum Beispiel 1%, 5%, oder 10%) muss man u(α) bzw. 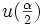$u(\tfrac{\alpha}{2})$ aus einer geeigneten Tabelle entnehmen. Bei einer Signifikanz von 5% ist 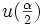$u(\tfrac{\alpha}{2})$ beispielsweise 1,960.

Die Nullhypothese (dass die beiden Zahlenreihen zur selben Grundgesamtheit gehören) wird abgelehnt, wenn beim einseitigen Test U1 < U bzw. U2 < U ist und beim zweiseitigen Test min(U) < U ist.

Es gibt auch Tabellen, aus denen man in Abhängigkeit von n₁ und n₂ den kritischen U-Wert entnehmen kann. Die folgende Tabelle ist gültig für 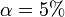$\alpha=5\%$ (zweiseitig) und 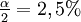$\tfrac{\alpha}{2}=2,5\%$ (einseitig).

Kritische U-Werte für den Mann-Whitney-Test

zweiseitig α = 0,05

einseitig $\tfrac{\alpha}{2} = 0,025$

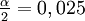
n1	n2
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	-
2	-	-
3	-	-	-
4	-	-	-	0
5	-	-	0	1	2
6	-	-	1	2	3	5
7	-	-	1	3	5	6	8
8	-	0	2	4	6	8	10	13
9	-	0	2	4	7	10	12	15	17
10	-	0	3	5	8	11	14	17	20	23
11	-	0	3	6	9	13	16	19	23	26	30
12	-	1	4	7	11	14	18	22	26	29	33	37
13	-	1	4	8	12	16	20	24	28	33	37	41	45
14	-	1	5	9	13	17	22	26	31	36	40	45	50	55
15	-	1	5	10	14	19	24	29	34	39	44	49	54	59	64
16	-	1	6	11	15	21	26	31	37	42	47	53	59	64	70	75
17	-	2	6	11	17	22	28	34	39	45	51	57	63	69	75	81	87
18	-	2	7	12	18	24	30	36	42	48	55	61	67	74	80	86	93	99
19	-	2	7	13	19	25	32	38	45	52	58	65	72	78	85	92	99	106	113
20	-	2	8	14	20	27	34	41	48	55	62	69	76	83	90	98	105	112	119	127
21	-	3	8	15	22	29	36	43	50	58	65	73	80	88	96	103	111	119	126	134
22	-	3	9	16	23	30	38	45	53	61	69	77	85	93	101	109	117	125	133	141
23	-	3	9	17	24	32	40	48	56	64	73	81	89	98	106	115	123	132	140	149
24	-	3	10	17	25	33	42	50	59	67	76	85	94	102	111	120	129	138	147	156
25	-	3	10	18	27	35	44	53	62	71	80	89	98	107	117	126	135	145	154	163
26	-	4	11	19	28	37	46	55	64	74	83	93	102	112	122	132	141	151	161	171
27	-	4	11	20	29	38	48	57	67	77	87	97	107	117	127	137	147	158	168	178
28	-	4	12	21	30	40	50	60	70	80	90	101	111	122	132	143	154	164	175	186
29	-	4	13	22	32	42	52	62	73	83	94	105	116	127	138	149	160	171	182	193
30	-	5	13	23	33	43	54	65	76	87	98	109	120	131	143	154	166	177	189	200
31	-	5	14	24	34	45	56	67	78	90	101	113	125	136	148	160	172	184	196	208
32	-	5	14	24	35	46	58	69	81	93	105	117	129	141	153	166	178	190	203	215
33	-	5	15	25	37	48	60	72	84	96	108	121	133	146	159	171	184	197	210	222
34	-	5	15	26	38	50	62	74	87	99	112	125	138	151	164	177	190	203	217	230
35	-	6	16	27	39	51	64	77	89	103	116	129	142	156	169	183	196	210	224	237
36	-	6	16	28	40	53	66	79	92	106	119	133	147	161	174	188	202	216	231	245
37	-	6	17	29	41	55	68	81	95	109	123	137	151	165	180	194	209	223	238	252
38	-	6	17	30	43	56	70	84	98	112	127	141	156	170	185	200	215	230	245	259
39	0	7	18	31	44	58	72	86	101	115	130	145	160	175	190	206	221	236	252	267
40	0	7	18	31	45	59	74	89	103	119	134	149	165	180	196	211	227	243	258	274

Literatur

• Sidney Siegel: Nichtparametrische statistische Methoden. Fachbuchhandlung für Psychologie, Eschborn bei Frankfurt am Main, 2. Ausgabe, 1985)
• Wilcoxon, Frank (1945): Individual Comparisons by Ranking Methods. Biometrics Bulletin 1: 80–83.
• Mann, Henry/Whitney, Donald (1947): On a test of whether one of two random variables is stochastically larger than the other. Annals of mathematical Statistics 18: 50-60.

Weblinks

• VassarStats Mann-Whitney-Test (engl., Möglichkeit zur Berechnung von Werten)
• Mann-Whitney U test (engl.)
• Mann-Whitney U Test (engl., Eingabeformular, rechnet U aus n1 und n2 oder Datenwerten aus)