MaxSort

Der Begriff Sortierlese oder Selection-Sort (englisch selection »Auswahl«, to sort »sortieren«), auch MinSort (von Minimum) bzw. MaxSort (von Maximum), Selectsort oder ExchangeSort (AustauschSort) genannt, bezeichnet einen naiven Sortieralgorithmus, der in-place arbeitet und in seiner Grundform instabil ist, wobei er sich auch stabil implementieren lässt. Die Komplexität von SelectionSort ist, in der Landau-Notation ausgedrückt, O(n²).

Prinzip

Sei S der sortierte Teil des Arrays und U der unsortierte Teil. Am Anfang ist S noch leer, U entspricht dem ganzen Array. Das Sortieren durch Auswählen funktioniert so:

Suche das kleinste Element in U und vertausche es mit dem ersten Element.

Danach ist das Array bis zu dieser Position sortiert. Das kleinste Element wird in S verschoben. S ist um ein Element gewachsen, U um ein Element kürzer geworden. Anschließend wird das Verfahren solange wiederholt, bis das gesamte Array abgearbeitet worden ist.

Alternativ sucht man das Maximum, also das Element mit dem größten Sortierschlüssel. Das Maximum wird dann mit dem letzten Element des Arrays vertauscht und man erhält ebenfalls ein sortiertes Teilarray der Länge 1, allerdings rechts, und ein unsortiertes Array der Länge n-1, diesmal links. Der Algorithmus wird dann auch auf das unsortierte Teilarray angewendet.

Zudem existieren auch Ansätze, in denen beide Varianten (MinSort und MaxSort) gemeinsam arbeiten, sprich während eines Durchlaufes das größte und das kleinste Element eines Arrays gesucht und dieses dann jeweils an den Anfang, bzw. an das Ende des Arrays, gesetzt werden. Dadurch hat man in der Regel eine Beschleunigung um den Faktor 2.

Beispiel

Es soll ein Array mit dem Inhalt [M | D | A | Z | G | Q] sortiert werden, wobei gilt: A < B < C < ... < Y < Z. Rot eingefärbte Felder deuten eine Tauschoperation an, blau eingefärbte Felder liegen im bereits sortierten Teil des Arrays.

M D A Z G Q	Das Minimum ist A. Vertausche also das 1. und das 3. Element
A D M Z G Q	Das Minimum des rechten Teilarrays ist D. Da es bereits an 2. Position ist, muss praktisch nicht getauscht werden
A D M Z G Q	Wir haben jetzt bereits ein sortiertes Teilarray der Länge 2. Wir vertauschen nun M und das Minimum G
A D G Z M Q	Wir vertauschen Z und M
A D G M Z Q	Wir vertauschen Z und Q
A D G M Q Z	Das Array ist jetzt fertig sortiert

Komplexität

Um ein Array mit n Einträgen mittels SelectionSort zu sortieren, muss n-1 Mal das Minimum bestimmt und ebenso oft getauscht werden.

Bei der ersten Bestimmung des Minimums sind n-1 Vergleiche notwendig, bei der zweiten n-2 Vergleiche usw.

Mit der gaußschen Summenformel erhält man die Anzahl der notwendigen Vergleiche:

$(n-1)+(n-2)+...+3+2+1 =\frac{(n-1)\cdot n}{2}=\frac{n^2}{2}-\frac{n}{2}$

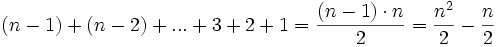
Man beachte, dass die exakte Schrittzahl dadurch, dass das erste Element (n − 1) ist, nicht genau der Darstellung der Gaußformel 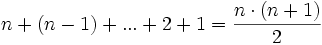$n+(n-1)+...+2+1 =\frac{n\cdot(n+1)}{2}$ entspricht.

SelectionSort liegt somit in der Komplexitätsklasse $\mathcal{O}(n^2)$.

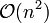Da zum Ermitteln des Minimums immer der komplette noch nicht sortierte Teil des Arrays durchlaufen werden muss, liegt SelectionSort nicht nur im schlechtesten Fall, sondern sogar in jedem Fall in dieser Komplexitätsklasse.

Implementierung in diversen Programmiersprachen

Java

public class SelectionSorter
{
    private int[] a;  // zu sortierendes Array
    private int n;    // Länge des Arrays
 
    // übernimmt die Referenz auf ein Array und sortiert es
    public void sort(int[] anArray)
    {
        a=anArray;
        n=a.length;
        selectionSort();
    }
 
    // sortiert das Array a mit Selectionsort
    private void selectionSort()
    {
        for (int i=0; i<n-1; i++)
        {
            int minpos=minimumPosition(i);
            swap(minpos, i);
        }
    }
 
    // findet die Position der kleinsten Zahl ab Position from
    private int minimumPosition(int from)
    {
        int minpos=from;
        for (int i=from+1; i<n; i++)
            if (a[i]<a[minpos]) 
                minpos=i;
        return minpos;
    }
 
    // vertauscht zwei Einträge im Array
    private void swap(int i, int j)
    {
        int temp=a[i];
        a[i]=a[j];
        a[j]=temp;
    }
}

C

//Parameter: Zeiger auf Feld, Index Startelement, Index Endelement
int findMinimum(int *feld, int start, int end)
{
	//Merker für Index des minimalen Elementes
	int minIdx;
	//Erstes Element ist vorerst das minimale Element
	minIdx = start;
 
	for ( int aktIdx = start + 1; aktIdx <= end; aktIdx++)
	{
		//Ist aktuelles Feldelement kleiner als das Bisherige?
		if ( feld[aktIdx] < feld[minIdx] )
			//Neues Minimum
			minIdx = aktIdx;
	}
 
	//Rückgabe des Index für minimales Feldelement
	return minIdx;
}
 
//Parameter: Zeiger auf Feld, Index der zu vertauschenden Elemente
void exchange(int *feld, int e1, int e2)
{
	//Merker für Tauschvorgang
	int tmp;
	//Tauschen
	tmp = feld[e1];
	feld[e1] = feld[e2];
	feld[e2] = tmp;
}
 
//Parameter: Zeiger auf Feld, Anzahl der Elemente
void selectionsort(int *feld, int anzahl)
{
	//Merker für Index des minimalen Elementes
	int minIdx;
 
	//Schleife zum Durchlaufen des Feldes
	for (int i = 0; i < anzahl; i++)
	{
		minIdx = findMinimum(feld, i, anzahl-1);
		exchange(feld, i, minIdx);
	}
}

C#

static void SelectionSort(out List<int> feld)
{
    // alle Zahlen durchlaufen
    for (int i = 0; i < feld.Count; i++)
    {
        // Position min der kleinsten Zahl ab Position i suchen
        int min = i;
        for (int j = i + 1; j < feld.Count; j++)
            if (feld[j] < feld[min])
                min = j;
 
        // Zahl an Position i mit der kleinsten Zahl vertauschen
        int tmp = feld[min];
        feld[min] = feld[i];
        feld[i] = tmp;
    }
}

Oberon

PROCEDURE SelectSort* ( VAR a : ARRAY OF INTEGER ; n : INTEGER );
    VAR
        i, j, min, temp : INTEGER;
    BEGIN
        FOR i := 0 TO n-2 DO
            min := i;
            FOR j := i+1 TO n-1 DO
                IF a[j] < a[min] THEN min := j END
            END;
            IF min # i THEN
                temp := a[i]; a[i] := a[min]; a[min] := temp;
            END
        END
    END SelectSort;

Pascal

{ Parameter: Zu sortierendes Array, das mit ganzen Zahlen belegt ist }
Procedure SelectionSort(Var Feld: Array Of LongInt);
Var
    i, j     : LongInt;  { Zaehlvariablen }
    Temp, Min: LongInt;  { Hilfsvariable, Position des Minimums }
Begin
    For i := Low(Feld) To High(Feld) Do
    Begin
        Min := i;
        For j := i+1 To High(Feld) Do
            If Feld[j] < Feld[Min] Then
                Min := j;
        Temp := Feld[Min];
        Feld[Min] := Feld[i];
        Feld[i] := Temp;
        inc(i);
    End;
End;  { Procedure SelectionSort }

Visual Basic

Sub SelectionSort()
    Dim Lowest As Integer, Temp As Integer, I As Integer, J As Integer
    For I = 0 To UBound(Feld) - 1
        Lowest = I
        For J = I + 1 To UBound(Feld)
            If Feld(J) < Feld(Lowest) Then
                Lowest = J
            End If
        Next J
        Temp = Feld(I)
        Feld(I) = Feld(Lowest)
        Feld(Lowest) = Temp
    Next I
End Sub

PHP

function selectionSort($array)
{
    for ($i=0; $i<count($array); $i++)
    {
        // Position des kleinsten Elements suchen
        $minpos=$i;
        for ($j=$i+1; $j<count($array); $j++)
            if ($array[$j]<$array[$minpos])
                $minpos=$j;
        // Elemente vertauschen
        $tmp=$array[$minpos];
        $array[$minpos]=$array[$i];
        $array[$i]=$tmp;
    }
    return $array;
}
 
 
//Zur Kontrolle
print_r(selectionSort(array('F', 'A', 'B', 'E', 'D', 'C', 'H', 'G')));

Python

def selectionsort(seq):
    for i in xrange(len(seq) - 1):
        k = i
        for j in xrange(i, len(seq)):
            if seq[j] < seq[k]:
                k = j
        seq[i], seq[k] = seq[k], seq[i]
    return seq       

Ruby

def selectionsort(list)
  0.upto(list.size-2) do |start|
    min = start
    (start+1).upto(list.size-1) do |i|
      min = i if list[i] < list[min]
    end
    list[start], list[min] = list[min], list[start]
  end
  list
end

Haskell

sSort :: (Ord a) => [a] -> [a]
sSort [] = []
sSort xs = minimum xs : sSort (delete (minimum xs) xs)
{- delete löscht das erste Auftreten eines Elements, dadurch wird er stabil und erlaubt doppelte Elemente -}

Smalltalk

Die erste Zeile gibt an, in welche Klasse man die Methoden einfügt.

!SequenceableCollection methodsFor: 'sorting' !
selectionSort
self withIndexDo: [:e :i|  self swap:i with: (self indexOf:(self last:self size-i+1) min) ]! !

Ergebnis: #(1 2 3 4) shuffled selectionSort → #(1 2 3 4)

Ada

begin
	for i in 1..n loop
		min:=A(i);
		pos:=i;
		for j in i+1..n loop
			if A(j)< min then
				min:=A(j);
				pos:=j;
			end if;
		end loop;
		A(pos):=A(i);
		A(i):=min;
	end loop;
end;

Eiffel

Aufgeteilt in zwei Features (arraymin und selectionsort), damit der Code übersichtlicher ist.

arraymin(array: ARRAY [INTEGER]; lower, upper: INTEGER) is
		-- Get index of Array minimum between lower and upper index
	local
		i, smallestsofar, index: INTEGER
	do
		from
			i:=lower
			smallestsofar := array.item (i)
			index := i
		until
			i+1 > upper
		loop
			if  array.item(i+1) < smallestsofar then
				smallestsofar := array.item(i+1)
				index := i+1
			end
			i := i + 1
		end
		 minindex := index
		 minitem := array.item (index)
	end

minindex: INTEGER
	--stores the index of the minimum with arraymin
minitem: INTEGER
	--stores the minimum of the value found with arraymin

selectionsort (x: ARRAY [INTEGER]) is
		-- sort Array x with selectionsort

	local
		count: INTEGER
		size: INTEGER
	do
		from
			count:=1
			size := x.count
		until
			count > size

		loop
			arraymin (x, count, size)
			x.put (x.item (count), minindex)
			x.put (minitem, count)
			count := count + 1
		end
	end

Scheme

(require (lib "list.ss"))
(define selection_sort
  (lambda (l)
    (if (empty? l) 
        '()
        (let ((m (apply min l)))
          (cons m (selection_sort (remove m l)))
         ))))

Logo

;Bestimmt Index des kleinsten Elements in a, geprüft ab Element start
to minIdx :start :a
 localmake "result :start
 localmake "i :start
 while [:i <= count :a] [
  if (item :i :a) < (item :result :a) [make "result :i]
  make "i :i + 1
 ]
 output :result
end

;Vertauscht im Array a das x-te mit dem y-ten Element
to swap :a :x :y
 localmake "hilf item :x :a
 setitem :x :a item :y :a
 setitem :y :a :hilf
end

;Sortiert das Array a
to selSort :a
 localmake "i 1
 while [:i < count :a] [
  swap :a :i minIdx :i :a
  make "i :i + 1
 ]
end

;Aufruf:
make "array {6 4 8 0 7 5 1}
selsort :array
show :array

Varianten

Heapsort arbeitet nach demselben Prinzip wie SelectionSort, benutzt jedoch die Eigenschaften eines Heaps, um das Minimum schneller zu bestimmen.

Es besteht die Möglichkeit MinSort und MaxSort miteinander zu kombinieren. Es wird dann gleichzeitig sowohl nach dem jeweils größten, als auch nach dem jeweils kleinsten Element gesucht.

Perl

sub minmax{
        my $n,$l,$i,$j;
        $n=$_;
        $l=int($#_/2);
        for($i=0;$i<=$l;$i++){
                for($j=$i+1;$j<$n;$j++){
                        if($_[$i]>$_[$n]){
                                ($_[$i],$_[$n])=($_[$n],$_[$i])
                        }
                        if($_[$j]<$_[$i]){
                                ($_[$i],$_[$j])=($_[$j],$_[$i])
                        }elsif($_[$j]>$_[$n]){
                                ($_[$j],$_[$n])=($_[$n],$_[$j])
                        }
                }$n--
        }return@_
}
@array=minmax(@array);
print"@array\n"

Python

# Zu Gunsten der Eleganz wurde teilweise auf Effizienz verzichtet.
def minmaxpos(liste):
    if len(liste) < 1:
        raise IndexError('Die Liste muss mindestens ein Element enthalten!')
    min, max = len(liste) - 1, len(liste) - 1
    for p in xrange(0, len(liste) - 1, 2):
        if liste[p] <= liste[p + 1]:
            kleiner, groeszer = p, p + 1
        else:
            kleiner, groeszer = p + 1, p
        if liste[kleiner] < liste[min]:
            min = kleiner
        if liste[groeszer] > liste[max]:
            max = groeszer
    return min, max
 
def maxpos(liste):
    max = 0
    for p in xrange(1, len(liste)):
        if liste[p] > liste[max]:
            max = p
    return max
 
def minmaxsort(liste):
    if len(liste) <= 1:
        return
    unter, ober = 0, len(liste) - 1
    if len(liste) % 2 == 0:# Die Anzahl der Elemente muss ungerade sein.
    # Ist sie gerade, so wird das letzte Element mit dem Maximum vertauscht und dann ignoriert.
        max = maxpos(liste)
        liste[ober], liste[max] = liste[max], liste[ober]
        ober -= 1
    while unter < ober:
        min, max = minmaxpos(liste[unter: ober + 1])# Minimum und Maximum der Restliste bestimmen
        min, max = min + unter, max + unter# unter wurde in der Funktion mit 0 adressiert
        # Minimum<->Untergrenze; Maximum<->Obergrenze
        if max == unter:# Da unter und min getauscht werden,
            max = min   # muss max mit dem ehemaligen min getauscht werden
        liste[min], liste[unter] = liste[unter], liste[min]
        liste[max], liste[ober] = liste[ober], liste[max]
        unter, ober = unter + 1, ober - 1# Grenzen einengen

Weblinks

• VisuSort Framework - Visualisierung diverser Sortieralgorithmen (Windows)
• http://www.inf.ethz.ch/~staerk/algorithms/SortAnimation.html Java Beispiele
• http://www.sortieralgorithmen.de/selectsort/index.html
• Erklärung und Code in C++