MaxiMin-Regel

Als Entscheidung unter Ungewissheit werden in der Entscheidungstheorie Entscheidungssituationen bezeichnet, bei denen zwar die Alternativen, die möglichen Umweltzustände und die Ergebnisse bei Wahl einer bestimmten Alternative und Eintritt eines bestimmten Umweltzustandes bekannt sind, in denen aber die Eintrittswahrscheinlichkeiten der Umweltzustände unbekannt sind. Diese werden manchmal auch Entscheidungen bei objektiver Unsicherheit genannt.

Allgemeines

Entscheidung unter Ungewissheit ist in der Entscheidungstheorie ein Unterfall der Entscheidung unter Unsicherheit. Entscheidungen unter Ungewissheit unterscheiden sich von Entscheidungen unter Risiko dadurch, dass bei letzteren die Wahrscheinlichkeiten für das Eintreten bestimmter Umweltzustände als bekannt vorausgesetzt werden oder zumindest durch eine Schätzung zugeordnet werden können.

Die Entscheidungssituation bei Entscheidungen unter Ungewissheit kann durch eine Ergebnismatrix dargestellt werden. Der Entscheider hat die Wahl zwischen verschiedenen Alternativen a_i, die abhängig von den möglichen Umweltzuständen s_j verschiedene Ergebnisse e_ij zur Folge haben. Allerdings weiß der Entscheider vorher nicht, mit welcher Wahrscheinlichkeit die Umweltzustände und damit die Ergebnisse eintreffen.

Entscheidungsregeln

Beispielhafte Entscheidungssituation

Beispiel: 100 € sollen für ein Jahr angelegt werden. Zur Wahl stehen: eine Aktie (a₁) oder der Sparstrumpf, der keine Zinsen abwirft (a₂). Die möglichen Umweltzustände sind: Der Aktienkurs steigt (s₁), er sinkt (s₂) oder er bleibt gleich (s₃).

Die Ergebnismatrix sieht dann zum Beispiel wie folgt aus:

	s1	s2	s3
a1	120	80	100
a2	100	100	100

Entscheidungen unter Ungewissheit können rational nach unterschiedlichen Regeln gefällt werden:

Maximin-Regel

Die Maximin-Regel, die nach Abraham Wald auch Wald-Regel genannt wird, ist sehr pessimistisch. Hierbei wird das jeweils ungünstigste Ereignis betrachtet, welches bei Wahl einer bestimmten Handlungsalternative i in den verschiedenen Umweltzuständen eintreten kann. Die Alternativen werden nur anhand dieses jeweils schlechtesten Ergebnisses (das jeweils bei verschiedenen Umweltzuständen eintreten kann) verglichen, alle anderen möglichen Ergebnisse einer Alternative werden nicht betrachtet.

$\max_i:\varphi_{ai}=\min_j e_{ij}$

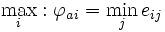
Im vorliegenden Beispiel wählt der Entscheider den Sparstrumpf (Alternative 2), da dieser unabhängig von den Umweltzuständen eine Auszahlung von 100 garantiert, während bei Alternative 1 im schlechtesten Fall (Kurs sinkt, Umweltzustand s2) am Ende des Jahres nur 80 zu Buche stehen. Aus diesen Zeilenminima wählt man anschließend das Maximum. Aus diesem Vorgehen leitet sich der Name der Entscheidungsregel ab.

Eine konkrete Anwendung der MaxiMin-Regel findet sich bei John Rawls in Eine Theorie der Gerechtigkeit. Eine Erweiterung der Maximin-Regel ist die Leximin-Regel von Amartya Sen^[1], wonach für den Fall, dass zwei Alternativen den jeweils schlechtesten Zustand aufweisen, diejenige auszuwählen ist, bei der der zweitschlechteste Fall den höchsten Wert aufweist, u.s.w. Durch diesen Zusatz wird vermieden, dass eine insgesamt schlechtere Version gewählt werden kann, nur weil sie dem Maximin-Prinzip entspricht.

Maximax-Regel

Die Maximax-Regel ist eine sehr optimistische Entscheidungsregel. Hierbei wird jede Alternative nur anhand des Ergebnisses, das beim jeweils für diese Alternative günstigsten Umweltzustand eintreten kann, beurteilt. Der Entscheider wählt also diejenige Handlungsalternative mit dem maximalen Zeilenmaximum.

$\max_i:\varphi_{ai}=\max_j e_{ij}$

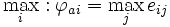
Im vorliegenden Beispiel wählt der Entscheider die Aktie (Alternative 1), da e₁₁ = 120 größer als e_{21 / 22 / 23} = 100.

Kritik an Maximin- und Maximax-Regel

Beide vorliegenden Regeln berücksichtigen nicht alle möglichen Ergebnisse einer Handlungsalternative, sondern greifen sich nur jeweils das beste (Maximax) oder das schlechteste (Maximin) Ergebnis einer Alternative heraus. Dies kann zu unerwünschten Ergebnissen führen, wie die folgenden Beispiele zeigen.

	s1	s2	s3	s...	s99	s100
a1	0	0	0	0	0	120
a2	119	119	119	119	119	119

Nach der Maximax-Regel würde hier die Alternative a₁ gewählt, da nur das Ergebnis im günstigsten Umweltzustand s₁₀₀ also e_1;100 = 120 betrachtet wird, was größer als 119 ist. Die in allen anderen Umweltzuständen eintretende Auszahlung von Null bei Alternative a₁ würde nicht berücksichtigt.

	s1	s2	s3	s...	s99	s100
a1	120	120	120	120	120	99
a2	100	100	100	100	100	100

Nach der Maximin-Regel würde hier die Alternative a₂ gewählt, da nur das jeweils im ungünstigsten Umweltzustand eintretende Ergebnis betrachtet wird, also für die Alternative a₁ das Ergebnis e_1;100 = 99 und bei Alternative a₂ 100. Die in allen anderen Umweltzuständen eintretende Auszahlung von 120 bei Alternative a₁ würde nicht berücksichtigt.

Hurwicz-Regel

Die Hurwicz-Regel, benannt nach Leonid Hurwicz, auch Optimismus/Pessimismus-Regel genannt, erlaubt Kompromisse zwischen pessimistischen und optimistischen Entscheidungsregeln, weil der Entscheidungsträger dabei seine persönliche und subjektive Einstellung durch den sogenannten Optimismusparameter λ (mit 0<=λ<=1) zum Ausdruck bringen kann.

Die jeweiligen Zeilenmaxima werden somit mit λ (das zwischen 0 und 1 liegt) und die jeweiligen Zeilenminima mit (1- λ) – d. h. dem in der Summe mit λ einen Wert von 1 ergebenden Betrag – multipliziert.

Je größer λ ist, um so optimistischer ist die Grundeinstellung, bei λ = 1 liegt die Anwendung der Maximax-Regel, bei λ = 0 die Anwendung der Maximin-Regel vor.

$\max_i:\varphi_{ai}=\lambda \cdot \max_j e_{ij}+(1-\lambda)\min_j e_{ij}$

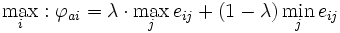
Im vorliegenden Beispiel wählt der Entscheider für λ > 0,5 die Aktie und für λ < 0,5 den Sparstrumpf.

Auch die Hurwicz-Regel betrachtet nicht alle möglichen Ergebnisse, sondern bewertet die Alternativen anhand eines gewichteten Mittelwerts ihres bestmöglichen und ihres schlechtmöglichsten Ergebnisses. Problematisch ist bei ihr weiterhin, dass die Wahl des Optimismusparameters stark stimmungsabhängig schwanken kann.

Beispiel:

bei λ = 0,3 würde man sich also für die Alternative a₂ entscheiden.

	s1	s2	s3	Hurwicz − Regel
a1	120	80	100	(120 x 0,3 + 80 x 0,7) = 92
a2	100	100	100	(100 x 0,3 + 100 x 0,7) = 100

Laplace-Regel

Die Laplace-Regel: Man nimmt an, dass die Wahrscheinlichkeiten für das Eintreten der möglichen Ergebnisse bei allen Wahlmöglichkeiten gleich sind. Die Wahlmöglichkeit, die dann das beste Ergebnis verspricht, wird ausgewählt, d.h. es wird diejenige Alternative gewählt, deren Erwartungswert maximal ist:

$\max_i:\varphi_{ai}=\frac{1}{n}\sum_j e_{ij}$

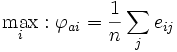
Die Laplace-Regel beruht auf folgender Annahme: Da keine Eintrittswahrscheinlichkeiten bezüglich der Umweltzustände bekannt sind, gibt es keinen Grund, anzunehmen, dass ein Umweltzustand wahrscheinlicher sei als ein anderer, daher müsse man von Gleichverteilung der Eintrittswahrscheinlichkeiten ausgehen. Damit berücksichtigt die Laplace-Regel sämtliche Umweltzustände bei der Bewertung der Alternativen. Im vorliegenden Beispiel ist der Entscheider indifferent zwischen der Aktie und dem Sparstrumpf.

Savage-Niehans-Regel

Die Savage-Niehans-Regel (auch Minimax-Regret-Regel): die Beurteilung der Handlungsalternativen basiert bei dieser Regel nicht auf dem unmittelbaren Nutzen der Ergebnisse, sondern auf deren Schadenswerten im Vergleich zum maximal möglichen Gewinn. Man wählt diejenige Alternative, welche den potentiellen Schaden minimiert 'Regel des kleinsten Schadens' oder des 'geringsten Bedauerns', engl. Minimal-Regret.

Im Beispiel: Wenn Umweltzustand 1 eintritt (Aktie steigt), dann hätte man bei Wahl des Sparstrumpfes 20 verloren (Opportunitätskosten). Wenn Umweltzustand 2 eintritt (Aktie sinkt), dann hätte man bei Wahl der Aktie 20 verloren. Bei Umweltzustand 3 ist es egal, was ich gewählt hätte, da beide Aktionen einen Schadenswert von 0 haben. Die Ergebnismatrix sieht dann wie folgt aus:

	s1	s2	s3
a1	0	20	0
a2	20	0	0

Um die beste Alternative zu finden muss man aus der obigen Tafel zeilenweise den größten Wert suchen (maximales Bedauern) und dann die Alternative (Zeile) wählen, die den kleinsten Wert aufweist (maximales Bedauern minimieren). Im obigen Beispiel ist das Maximum beider Alternativen jeweils 20, daher sind beide Alternativen gerade gleich gut.

Krelle-Regel

Eine weitere Entscheidungsregel wurde von Wilhelm Krelle vorgeschlagen. Sie beruht darauf, dass alle mit einer Aktion a_i verknüpften Nutzenwerte u_i1, u_i2 ,... ,u_in mit einer für den Entscheidungsträger relevanten Unsicherheitspräferenzfunktion ω transformiert werden und anschließend addiert werden.

$\Phi(a_i)=\sum^n_{j=1}\omega(u_{ij})$

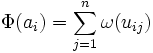
Die beste Alternative ist nun jene mit dem größten Gütemaß.

Erfahrungskriterium von Hodges und Lehmann

Diese Regel bildet einen Kompromiss zwischen der Maximin-Regel und der Bayes-Regel zu einer a-priori-Größe π. Zusätzlich wird der Vertrauensparameter λ eingeführt, der angibt, in welchem Maße der Entscheidungsträger der a-priori-Wahrscheinlichkeit vertraut.

Literatur

• v. Zwehl, W., Entscheidungsregeln, in: Handwörterbuch der Betriebswirtschaft, Teilband 1, 5. Aufl., Schäffer-Poeschel, 1993
• Bamberg, G., Coenenberg A., Betriebswirtschaftliche Entscheidungslehre, 13. Auflage, Verlag Vahlen, 2006

Einzelnachweise

1. ↑ Amartya Sen: Equality of What?, in: S. Murrin (Hrsg): The Tanner Lectures on Human Values, Cambridge University Press 1980, 196-220, auch in: Amartya Sen: Choice, Welfare and Measurement, Oxford 1982