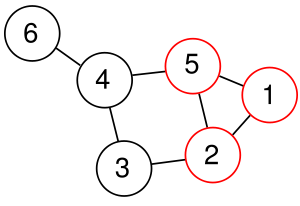
- Maximale Clique
-
Knotenüberdeckungen, Cliquen und stabile Mengen sind Begriffe der Graphentheorie und bezeichnen spezielle Teilmengen von Knoten in Graphen. Das Finden von minimalen Knotenüberdeckungen und größten Cliquen bzw. stabilen Mengen gilt als algorithmisch schwierig (NP-vollständig). Da diese Probleme eng miteinander verwandt sind, werden sie in diesem Übersichtsartikel zusammen dargestellt.
Inhaltsverzeichnis
Definitionen
Sei G=(V,E) ein ungerichteter Graph ohne Mehrfachkanten und U eine Teilmenge von V.
- Man bezeichnet U als Clique von G, wenn für je zwei beliebige verschiedene Knoten v und w aus U gilt, dass sie durch eine Kante miteinander verbunden sind.
- Gilt hingegen stets für je zwei beliebige verschiedene Knoten v und w aus U, dass sie nicht benachbart sind, so nennt man U eine stabile bzw. unabhängige Menge (Independent Set) von G.
- Enthält jede Kante von E wenigstens einen Knoten aus U, so nennt man U eine Knotenüberdeckung (Vertex Cover) von G.
Eine Clique bzw. stabile Menge U von G nennt man maximal, wenn man keinen weiteren Knoten v aus V zu U hinzufügen kann, so dass U zusammen mit v eine Clique bzw. stabile Menge ist. Gibt es in G keine Clique bzw. stabile Menge, die mehr Elemente als U enthält, so nennt man U größte Clique bzw. größte stabile Menge. Die Anzahl der Elemente einer größten Clique bzw. stabilen Menge nennt man Cliquenzahl bzw. Stabilitäts- oder Unabhängigkeitszahl. Die Anzahl der Knoten einer kleinsten Knotenüberdeckung von G nennt man Knotenüberdeckungszahl von G.
Statt über Teilmengen von V definiert man Cliquen oder stabile Mengen auch als spezielle Teilgraphen.
Als Cliquenüberdeckung von G der Größe k bezeichnet man eine Partition der Knotenmenge V(G) in k paarweise disjunkte Cliquen V1,V2,...,Vk.
Gerichtete Graphen oder solche mit Mehrfachkanten sind nicht Gegenstand derartiger Betrachtungen, da es nicht auf die Richtung oder Vielfachheit der Kanten ankommt.
Wichtige Aussagen und Sätze
- Die Knotenüberdeckungszahl eines Graphen ist mindestens so groß wie seine Paarungszahl, da die Knoten der Kanten einer größten Paarung nur zu einer Paarungskante inzident sein können.
- Andererseits kann die Knotenüberdeckungszahl höchstens so groß sein, wie das 2-fache der Paarungszahl, da die Knoten aller Paarungskanten eine gültige Knotenüberdeckung ergeben.
- In bipartiten Graphen stimmen Knotenüberdeckungszahl und Paarungszahl überein.
Probleme und Komplexität
Definition der Probleme
Das Entscheidungsproblem zu einem Graphen G und einer natürlichen Zahl k zu entscheiden, ob G eine Clique der Größe mindestens k enthält, wird Cliquenproblem genannt. Das zugehörige Optimierungsproblem fragt nach der Cliquenzahl eines Graphen. Das zugehörige Suchproblem fragt nach einer größten Clique. Diese drei Probleme sind polynomiell äquivalent.
Das Entscheidungsproblem zu einem Graphen G und einer natürlichen Zahl k zu entscheiden, ob G eine Knotenüberdeckung der Größe höchstens k enthält, wird Knotenüberdeckungsproblem genannt. Das zugehörige Optimierungsproblem fragt nach der Knotenüberdeckungszahl eines Graphen. Das zugehörige Suchproblem fragt nach einer kleinsten Knotenüberdeckung.
Analog ist das Stabilitätsproblem über stabile Mengen definiert.
Nachweis der NP-Schwere
Alle drei Probleme sind NP-vollständig. Die zugehörigen Optimierungs- und Suchprobleme sind NP-äquivalent. Die NP-Schwere des Stabilitätsproblems lässt sich dabei leicht durch Reduktion des Cliquenproblems auf das Stabilitätsproblem zeigen, indem man den Komplementgraphen bildet. Die NP-Schwere des Knotenüberdeckungsproblems folgt aus dem Satz, dass die Stabilitätszahl eines Graphen immer der Anzahl Knoten eines Graphen abzüglich seiner Knotenüberdeckungszahl entspricht, denn das Komplement einer kleinsten Knotenüberdeckung ist immer eine größte stabile Menge und umgekehrt. Für den Nachweis der NP-Schwere des Cliquenproblems existiert eine Reduktion von 3-SAT auf das Cliquenproblem.
In Polynomialzeit lösbare Fälle
König konnte jedoch schon 1931 zeigen, dass in bipartiten Graphen die Knotenüberdeckungszahl der Paarungszahl entspricht (Satz von König). Für das Problem, eine größte Paarung zu finden, gibt es aber einen polynomiellen Algorithmus. In bipartiten Graphen lässt sich daher auch eine kleinste Knotenüberdeckung und eine größte stabile Menge in polynomieller Zeit berechnen.
Eine größte Clique lässt sich entsprechend der obigen Reduktion in polynomieller Zeit berechnen, wenn der Komplementgraph bipartit ist.
Tatsächlich gilt sogar etwas stärker, dass Cliquenzahl, Stabilitätszahl und Knotenüberdeckungszahl in perfekten Graphen in polynomieller Zeit berechnet werden können. Da die Farbzahl und die Cliquenzahl in solchen Graphen identisch sind, ist auch ihre Farbzahl in polynomieller Zeit berechenbar.
Die Berechnung einer maximalen Clique bzw. stabilen Menge gelingt bereits mit einem einfachen Greedy-Algorithmus.
Approximation einer Knotenüberdeckung
Es existiert ein Approximationsalgorithmus, der eine Knotenüberdeckung mit Güte 2 berechnet. Es ist kein besserer Algorithmus mit fester Güte bekannt.
Der Algorithmus berechnet eine nicht-erweiterbare Paarung M in G. Da eine derartige Paarung immer eine Knotenüberdeckung darstellt und höchstens doppelt so groß ist wie eine minimale Knotenüberdeckung, berechnet der Algorithmus eine Knotenüberdeckung mit Güte 2.
G = (V, E): Graph approx_vertex_cover(G) 1 K
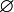 2 solange E
2 solange E 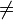
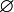 :
3 wähle eine beliebige Kante e = {u,v} aus E
4 K
:
3 wähle eine beliebige Kante e = {u,v} aus E
4 K  K
K  {u,v}
5 entferne alle Kanten aus E, die inzident zu u oder v sind
6 return K
{u,v}
5 entferne alle Kanten aus E, die inzident zu u oder v sind
6 return K
Der Algorithmus hat bei einer geeigneten Datenstruktur eine Laufzeit von O(|E|).
Wikimedia Foundation.