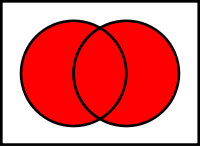
Disjunktion

Venn-Diagramm von $A \or B$
Die Vereinigung von Mengen wird über die Disjunktion definiert

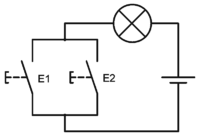
Technische Realisierung der nicht-ausschließenden Disjunktion im OR-Gatter:
Wenn Taster E1 oder E2 betätigt wird, leuchtet die Lampe.
Dieses logische Oder umfasst den Fall, dass beide gedrückt werden.

Disjunktion („Oder-Verknüpfung“, von lat. disiungere „trennen, unterscheiden, nicht vermengen“), Alternative und Adjunktion (von lat. adiungere, „anfügen, verbinden“) sind in der Logik die Bezeichnungen für zwei Typen von Aussagen, bei denen je zwei Aussagesätze durch ein ausschließendes oder oder durch ein nichtausschließendes oder verbunden sind:

1. Die nicht-ausschließende Disjunktion (Alternative, Adjunktion) „A oder B (oder beides)“ sagt aus, dass mindestens eine der beiden beteiligten Aussagen wahr ist. Sie ist also nur dann falsch, wenn sowohl A als auch B falsch sind.
2. Die ausschließende Disjunktion (Kontravalenz, exklusives Oder, XOR) „(entweder) A oder B (aber nicht beides)“ sagt aus, dass genau eine der beiden beteiligten Aussagen wahr ist (wenn die Disjunktion wahr ist). Die ausschließende Disjunktion ist daher falsch, wenn entweder beide beteiligten Aussagen falsch oder wenn beide beteiligten Aussagen wahr sind. Die ausschließende Disjunktion wird auch Kontravalenz genannt und unter diesem Stichwort näher behandelt.
3. Nur gelegentlich wird auch die nicht-ausschließende Disjunktion der Verneinungen der beteiligten Aussagen als Disjunktion von A und von B bezeichnet, das heißt die Aussage „nicht A oder nicht B (oder beides)“ beziehungsweise äquivalent „nicht (A und B)“. Diese Verbindung wird u.a. Shefferscher Strich, NAND oder Exklusion (im Sinne der Logik) genannt. Sie entspricht dem mengentheoretischen Begriff disjunkt.^[1]

Die Teilaussagen einer Disjunktion beziehungsweise einer Adjunktion werden Disjunkte beziehungsweise Adjunkte, das die Teilaussagen verknüpfende Wort („oder“) wird Disjunktor beziehungsweise Adjunktor genannt. Seltener gebrauchte Bezeichnungen für die Disjunktion lauten Kontrajunktion, Bisubtraktion und Alternation. Umgangssprachlich spricht man auch davon, zwei Aussagen zu verodern (engl. oring), wenn man sie disjunktiv verknüpft.

Die nicht-ausschließende Disjunktion

Die nicht-ausschließende Disjunktion (Alternative, Adjunktion) ist eine zusammengesetzte Aussage vom Typ „A oder B (oder beides)“; sie sagt aus, dass mindestens eine der beiden beteiligten Aussagen wahr ist.

Schreibweise

$A \or B$

In der polnischen Notation wird für die Disjunktion der Großbuchstabe A verwendet:

Aab

Eine Möglichkeit, um sich die Symbole für Disjunktion und Konjunktion zu merken und voneinander zu unterscheiden: Das nicht-ausschließende Oder, A ∨ B, erinnert an den Buchstaben „v“; das lateinische Wort für das nicht-ausschließende Oder lautet „vel“, fängt also mit „v“ an.

Die Wahrheitstabelle für die vel-Funktion als Wahrheitswertefunktion der nicht-ausschließenden Disjunktion ist damit:

A	B	$A \or B$
wahr	wahr	wahr
wahr	falsch	wahr
falsch	wahr	wahr
falsch	falsch	falsch

Eine Disjunktion ist ein Boolescher Ausdruck, sie ist assoziativ und kommutativ.

Aus dem Gesagten folgt:

• Ist A falsch und ist B falsch, so ist die Disjunktion falsch; in jedem anderen Fall ist sie wahr.
• Ist die Disjunktion falsch, so ist sowohl A als auch B falsch.
• Ist die Disjunktion wahr, muss eine der folgenden Möglichkeiten vorliegen:
  1. beide Disjunkte sind wahr
  2. A ist falsch und B ist wahr oder
  3. A ist wahr und B ist falsch

Beispiel

Die Aussage „Napoleon reist über Berlin nach Moskau, oder Napoleon reist über Rom nach Moskau“ besteht aus folgenden Teilen:

• der Teilaussage/dem Disjunkt A: „Napoleon reist über Berlin nach Moskau.“
• dem Disjunktor „oder“
• der Teilaussage/dem Disjunkt B: „Napoleon reist über Rom nach Moskau.“

Keine der beiden Teilaussagen schließt eine andere aus: Napoleon könnte über Berlin nach Moskau fahren, er könnte über Rom nach Moskau fahren, und er könnte jede beliebige andere Route wählen, die über mindestens eine dieser beiden Städte führt – ja sogar jede Route, die über beide Städte führe.

Die ausschließende Disjunktion

Hauptartikel: Kontravalenz

Die ausschließende Disjunktion (Kontravalenz, XOR) ist eine zusammengesetzte Aussage, bei der zwei Aussagen mit der Formulierung „entweder – oder (aber nicht beides)“ verknüpft werden, zum Beispiel die Aussage „Anna studiert entweder Französisch oder sie studiert Spanisch (aber nicht beides).“ Im Unterschied zur nicht ausschließenden Disjunktion ist damit der Fall, dass beide Teilaussagen wahr sind – im Beispiel also der Fall, dass Anna sowohl Französisch als auch Spanisch studiert, – ausgeschlossen. Der lateinische Ausdruck für dieses ausschließende Oder lautet „aut – aut“.

Die Wahrheitstabelle für die aut-Funktion als Wahrheitswertefunktion der ausschließenden Disjunktion ist damit:

A	B	$A ~ \dot\or ~ B$
wahr	wahr	falsch
wahr	falsch	wahr
falsch	wahr	wahr
falsch	falsch	falsch

Ableitungen im Kalkül des natürlichen Schließens

$\vee E:\ \frac{A}{A \vee B}\qquad \frac{A}{B \vee A}$

Aus einer Aussage A kann die Disjunktion A oder B geschlossen werden. ^[2][3]

Für die durch die Disjunktion zur bereits gegebenen Aussage A hinzugefügte Aussage B müssen keine vorherigen Voraussetzungen erfüllt sein, wie die folgende Beispielableitung zeigt.^[4]

Zeile	Aussage	Regel
1	$P\$	Prämisse
2	$P \vee Q$	1 $\vee E$ (Einführung der Disjunktion)

Zur Auflösung einer Disjunktion muss aus beiden Teilen der Disjunktion dieselbe Aussage hergeleitet werden können.^[4]

Zeile	Aussage	Regel
1	$(R \wedge Q)$$\vee$$(\lnot$$R \wedge Q)$	Prämisse
2	$R \wedge Q$	Annahme
3	$Q\$	$\wedge B$ (Und-Beseitigung)
4	$R \wedge Q \rightarrow Q$	2,3 $\rightarrow E$ (Implikations-Einfügung)
5	$\lnot R \wedge Q$	Annahme
6	$Q\$	5 $\wedge B$ (Und-Beseitigung)
7	$\lnot R \wedge Q \rightarrow Q$	5,6 $\rightarrow E$ (Implikations-Einfügung)
8	$Q\$	1,4,7 $\wedge B$ (Disjunktions-Beseitigung)

Bedeutungen des natürlichsprachlichen "oder"

• Siehe dazu: oder

Quellen

1. ↑ Kuno Lorenz: „Disjunktion“, in: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. Band 1. Stuttgart: Metzler 1995, ISBN 3-476-02012-6, Seite 491
2. ↑ vgl. Principia Mathematica 1.3
3. ↑ Esther Ramharter, Georg Riekh: Die Principia Mathematica auf den Punkt gebracht. ÖBV hpt, Wien 2006 S. 20
4. ↑ ^{a b} Niko Strobach: Einführung in die Logik. WBG Darmstadt, Darmstadt 2011, 2. Auflage S. 58

Siehe auch

• De Morgansche Regel
• Oder-Gatter, XOR-Gatter, XNOR-Gatter
• Aussagenlogik

Weblinks

• Ray Jennings: Disjunction, in: Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)