Maßstabparadoxon

Das Maßstabsparadoxon ist in der Speziellen Relativitätstheorie ein scheinbares Paradoxon, welches das Gegenstück zum Zwillingsparadoxon darstellt und auf der Längenkontraktion beruht.

Das Paradoxon

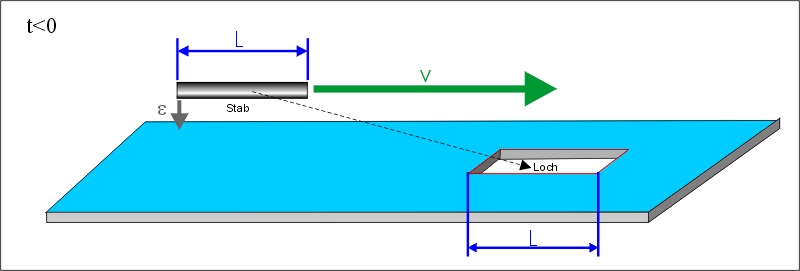
Ein Stab der Länge L bewege sich mit einer Geschwindigkeit v parallel zu einem ruhenden Loch, das ebenfalls die Breite L besitzt. Gleichzeitig bewegt sich der Stab noch mit einer kleinen, senkrechten Geschwindigkeit ε auf das Loch zu:

(Für die beiden einleitenden Abbildungen werde v so klein gegen die Lichtgeschwindigkeit c angenommen, dass keine relativistischen Effekte hervortreten.)

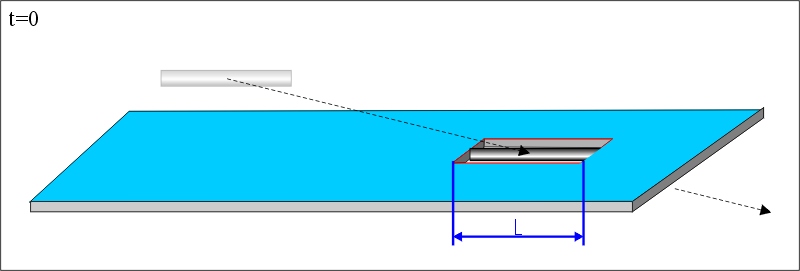
Zu einem geeigneten Zeitpunkt t=0 durchquert der Stab parallel das ruhende Loch:

Fall (A) Der Stab bewegt sich parallel auf das ruhende Loch zu

Vom Bezugssystem des ruhenden Lochs aus betrachtet erscheint der schnell (hier mit ca. v=0.94c) bewegte Stab durch die Längenkontraktion verkürzt auf die Länge L’ < L und passt damit bequem durch das Loch:

Fall (B) Das Loch bewegt sich auf den ruhenden Stab zu

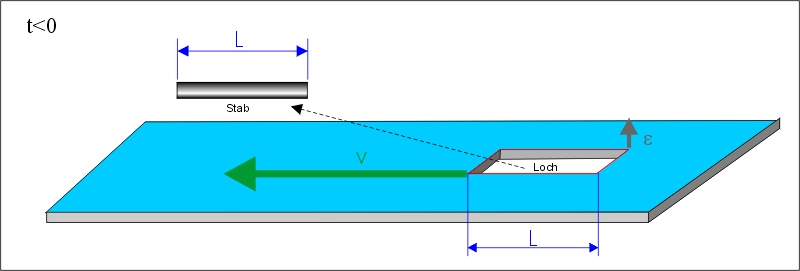
Betrachtet man die Situation allerdings vom mitbewegten System des Stabes aus, so ruht der Stab und das Loch bewegt sich relativ zum Stab mit der hohen Geschwindigkeit v auf den Stab zu: (In der oberen Abbildung bei t<0 wird das Loch noch in der Länge L gezeigt, die es in Ruhe hat, bevor es auf v beschleunigt wird.)

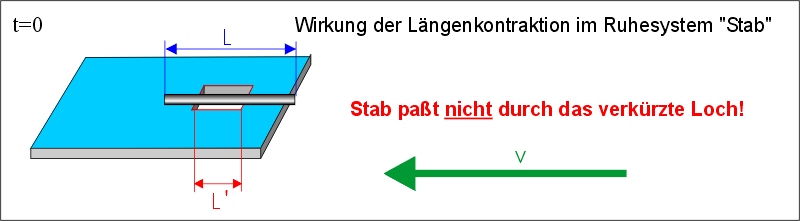
Vom nun als ruhend angesehenen Stab aus betrachtet, der in diesem Ruhesystem die Länge L besitzt, wirkt sich die Längenkontraktion jetzt auf das bewegte Loch aus, das nur noch die Breite L’ < L besitzt, so dass der Stab nicht mehr quer durch das Loch passt:

Das ist aber ein Widerspruch . Die Abmessungen können zwar wechselseitig verkürzt zueinander erscheinen, die Aussage, dass der Stab das Loch passiert, aber kann nicht von der Wahl des Bezugssystems abhängig gemacht werden; sonst wäre die Relativitätstheorie widersprüchlich und falsch.

Die Auflösung des Paradoxon

Die Beschreibung Fall (A) (Der Stab bewegt sich parallel auf das ruhende Loch zu) entspricht der Realität und ist richtig dargestellt. Die Beschreibung Fall (B) (Das Loch bewegt sich auf den ruhenden Stab zu) wurde in der vorangestellten Darstellung nicht vollständig richtig nach den Gesetzen der Lorentz-Transformation durchgeführt und erzeugt damit das scheinbare Paradoxon, das so gar nicht existiert. Bei der Transformation zum System im Fall (B) muss noch berücksichtigt werden, dass sich nicht nur die Ortskoordinaten entsprechend der Lorentz-Transformation ändern und so direkt zur Längenkontraktion führen, sondern dass auch die Zeit transformiert werden muss. Dadurch ändert sich aber auch die Sicht darauf, welche Ereignisse als gleichzeitig erscheinen. Im Fall (A) (ruhendes Loch) durchquert der Stab das Loch parallel, was bedeutet, dass sich das vordere und das hintere Ende des Stabes gleichzeitig zum Zeitpunkt t=0 durch das Loch bewegen. Dabei durchquere das hintere Ende des Stabes das Loch am Ort x=0, das vordere Ende des Stabes am Ort x₁. Im Fall (B) bleibt diese Durchtritts-Gleichzeitigkeit an den beiden aktuellen Lochrand-Orten aber nicht erhalten, sondern die Zeit t’ im Stab-Ruhesystem berechnet sich nach der Lorentz-Transformation:

$t^{'}=\frac{t-\frac{v}{c^2}\cdot x}{\sqrt{1-\frac{v^2}{c^2}}}$

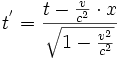
Wenn nun das hintere Ende des Stabes zum Zeitpunkt t=0 und am Ort x=0 das Loch durchquert, so geschieht das zu folgender Zeit im Stab-Ruhesystem:

$t^{'}=\frac{0-\frac{v}{c^2}\cdot 0}{\sqrt{1-\frac{v^2}{c^2}}}=0$

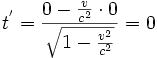
Für das vordere Ende des Stabes (zum Zeitpunkt t=0, am Ort x₁ im Loch) geschieht das zu folgender Zeit im Stab-Ruhesystem:

$t^{'}=\frac{0-\frac{v}{c^2}\cdot x_1}{\sqrt{1-\frac{v^2}{c^2}}} =\frac{-\frac{v}{c}\cdot x_1}{\sqrt{c^2-v^2}}&amp;amp;lt;0$

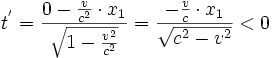
Das vordere Ende des Stabes hat also das Loch viel früher durchstoßen als das hintere Ende des Stabes (betrachtet im System, das sich mit dem Stab mitbewegt). Dass das vordere Ende des „ruhenden“ Stabes das heranfliegende Loch zuerst durchquert, bedeutet anschaulich, dass das Loch nicht mehr parallel zum Stab fliegt, sondern verkippt erscheint, so dass sich korrekter Weise das folgende transformierte Bild für den Fall (B) (Das Loch bewegt sich auf den ruhenden Stab zu) ergibt:

Stab und Loch fliegen in diesem System nicht mehr parallel aufeinander zu! Was lernt man nun daraus? Erstens: Gleichzeitige Ereignisse in einem Inertialsystem laufen in einem anderen unterschiedlich schnell bewegten Inertialsystem nicht ebenfalls gleichzeitig ab, und zweitens sind „parallele“ Geraden im anderen Inertialsystem nicht mehr parallel: Der Winkel zwischen zwei Raumrichtungen wird von zwei sich relativ zueinander bewegenden Beobachtern unterschiedlich gemessen!

Anmerkung

Die Argumentation kann auch anders herum durchgeführt werden: Geht man von einem ruhenden Stab aus, auf den sich tatsächlich ein Loch parallel zu bewegt, dann erzeugt die Transformation in das System des ruhenden Lochs (Fall (A)) nun die Verkippung des Stabes ( In der vorherigen Darstellung war es genau umgekehrt, dort wurde das Loch verkippt und nicht der Stab). Wie man es auch betrachtet, das Maßstabsparadoxon lässt sich so in jedem Fall auflösen und die Relativitätstheorie bleibt weiterhin widerspruchsfrei!

Siehe auch

• Bellsches Raumschiffparadoxon
• Garagenparadoxon

Literatur

• Ulrich E. Schröder: Spezielle Relativitätstheorie, Verlag Harri Deutsch, 2005, ISBN 3-8171-1724-8
• Richard Lenk: Brockhaus-abc-PHYSIK, Band 2, 2.Auflage, F.A. Brockhaus Verlag Leipzig, 1989, ISBN 3-325-00192-0