Bellsches Raumschiffparadoxon

Das bellsche Raumschiffparadoxon ist ein Paradoxon zur Längenkontraktion in der Relativitätstheorie, das 1976 von John Bell beschrieben wurde. Die zugrunde liegende Frage wurde allerdings schon seit den zwanziger Jahren des 20. Jahrhunderts untersucht. Für ähnliche Paradoxien, siehe Paradoxon der Längenkontraktion und Ehrenfestsches Paradoxon.

Das Paradoxon

Erläuterung

Der Vorgang aus der Sicht des ruhenden Beobachters: Oben die beiden Raketen beim Start und unten bei 60 % der Lichtgeschwindigkeit. Der Abstand L bleibt gleich, die beiden Raketen und das Seil erfahren dagegen eine Längenkontraktion auf 80 % ihrer Länge im Ruhezustand, so dass das Seil reißt.

Die Längenkontraktion, auch Lorentzkontraktion genannt, ist ein Phänomen der relativistischen Physik. Jeder bewegte Maßstab ist in Bewegungsrichtung kürzer als ein gleicher, ruhender Maßstab. Diese Verkürzung entzieht sich unserer Alltagserfahrung, da sie sich erst bei Geschwindigkeiten bemerkbar macht, die im Vergleich zur Lichtgeschwindigkeit ins Gewicht fallen.

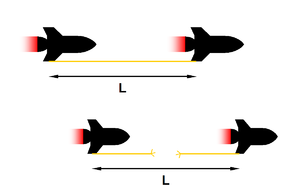
John Bell betrachtete dazu das folgende Gedankenexperiment: Zwei Raumschiffe beginnen, von einem ruhenden Beobachter gesehen, gleichzeitig aus dem Stand heraus zu beschleunigen und zwar in dieselbe Richtung, parallel zu ihrer Verbindungslinie. Zwischen beiden ist ein Seil gespannt, das bei der geringsten Dehnung reißt. Reißt das Seil, wenn seine Befestigungspunkte und jedes Teilstück des Seils in genau gleicher Weise bis zur selben Endgeschwindigkeit beschleunigt werden?

Da die Befestigungspunkte gleich beschleunigt werden, bleibt ihr Abstand L für den ruhenden Beobachter unverändert. Das Seil ist bewegt und wegen der Längenkontraktion kürzer als in Ruhe. In Ruhe muss es daher länger als L sein, um vom einen Befestigungspunkt zum anderen zu reichen. Das Seil reißt.

Dieses Ergebnis scheint widersprüchlich zu sein. Denn wenn aus Sicht der Raketenbesatzungen die Beschleunigungen gleich sind, dann ändert sich ihr Abstand nicht. Und da das Seil gegenüber den Besatzungen ruht, ändert es nicht seine Länge und reißt nicht.

Die Auflösung dieses scheinbaren Widerspruchs ist, dass aus der Sicht der Besatzungen beide Beschleunigungen aufgrund der Relativität der Gleichzeitigkeit nicht gleich sind. Für beide Besatzungen beschleunigt die hintere Rakete langsamer und erreicht erst nach der vorderen Rakete ihre Endgeschwindigkeit. Wird beispielsweise jedes Triebwerk zweimal kurz gezündet, und finden beide Schubphasen für den ruhenden Beobachter gleichzeitig statt, dann findet der zweite Schub für die dann schon bewegten Besatzungen nicht gleichzeitig statt, sondern bei der vorderen Rakete früher als bei der hinteren. Die Schübe ereignen sich aus Sicht der Besatzungen bei der vorderen Rakete in kürzerer Zeit, sie ist in kürzerer Zeit beschleunigt und daher am Ende bei gleicher Endgeschwindigkeit weiter von der hinteren Rakete entfernt als vor der Beschleunigung. Auch beide Besatzungen sehen das Seil reißen.

Herleitung

Formal sieht dieser Zusammenhang so aus: Es seien folgende Ruhelängen für das Raketen-Seil-Ensemble gegeben: L1 für die Länge beider Raketen, L2 für die Länge zwischen den Raketen, und L3 für die Länge des Seiles. Diese werden nun beschleunigt und kommen im Inertialsystem S' zur Ruhe: Nach Abschluss der Beschleunigung sind in S' sowohl L1' und L3' gleich geblieben, jedoch L2' ist aufgrund des Zurückbleibens der zweiten Rakete größer geworden, nämlich gemäß der in der Lorentz-Transformation enthaltenen Relativität der Gleichzeitigkeit um folgenden Wert:

$L2'=\frac{L2}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$

Da die Länge des Seils L3' gleich geblieben ist während L2' größer geworden ist, reißt das Seil. Wegen der Lorentzkontraktion sind nun alle Ruhelängen in S' für den in S verbliebenen Beobachter kontrahiert gemäß folgender Beziehungen:

$L1_{neu}=L1'\cdot\sqrt{1-\frac{v^{2}}{c^{2}}}$

$L2_{neu}=L2'\cdot\sqrt{1-\frac{v^{2}}{c^{2}}}=L2$

$L3_{neu}=L3'\cdot\sqrt{1-\frac{v^{2}}{c^{2}}}$

Die sich dabei ergebende Übereinstimmung von L2_neu mit L2 wird verständlich, wenn berücksichtigt wird, dass sich diese Kontraktion auf die neue Ruhelänge L2' zwischen den Raketen bezieht, welche wie oben errechnet um $1/\sqrt{1-v^{2}/c^{2}}$ größer als L2 ist. Da L2' wiederum um denselben Faktor in S kontrahiert gemessen wird, stimmt die sich daraus ergebende Länge L2_neu mit der vor dem Start gemessenen Länge L2 überein. D. h. die Tatsache, dass in S der Abstand zwischen den beiden Raketen aufgrund der gleichen Beschleunigung unverändert bleibt, ist in Übereinstimmung mit der Lorentzkontraktion bewegter Längen. Und da das Seil und somit L3_neu kleiner geworden ist, während L2_neu unverändert geblieben ist, reißt auch hier das Seil.

Geschichte

Bereits 1959 beschrieben E. Dewan und M. Beran eine Variante des zugrunde liegenden Problems korrekt. Das Ergebnis wurde in von Zeit zu Zeit wieder aufkommenden Debatten in Frage gestellt. 1962 veröffentlichte P. J. Nawrocki einen Aufsatz, der der Analyse von E. Dewan und M. Beran widersprach. E. Dewan verteidigte seine Analyse 1963. 1976 beschrieb John Bell das Problem, das seitdem das bellsche Raumschiffparadoxon genannt wird. Bell bezog sich dabei auf eine Diskussion des Paradoxons im CERN-Cafe. Der Standarderklärung widersprach ein namhafter Experimentalphysiker und auch in der anschließenden Umfrage in der Theorie-Abteilung des CERN war eine Mehrheit spontan der Meinung, das Seil würde nicht reißen^[1]. T. Matsuda und A. Kinoshita berichteten 2004 von einer regen Kontroverse in japanischen Physik-Journalen, nachdem sie dort die von ihnen ebenfalls vertretene Standarderklärung des Paradoxons (siehe oben) veröffentlicht hatten. Matsuda und Kinoshita schlossen mit der Feststellung, dass es selbst nach hundert Jahren Relativitätstheorie immer noch Physiker gäbe, welche die wirkliche Bedeutung der Längenkontraktion nicht verstanden hätten.

Literatur

• E. Dewan and M. Beran, Note on stress effects due to relativistic contraction, American Journal of Physics, 27 (1959) 517–518; doi:10.1119/1.1996214.
• P. J. Nawrocki, Stress Effects due to Relativistic Contraction, American Journal of Physics, 30 (1962) 771–772; doi:10.1119/1.1941785.
• E. M. Dewan, Stress Effects due to Lorentz Contraction, American Journal of Physics, 31 (1963) 383–386; doi:10.1119/1.1969514.
• J. S. Bell, How to teach special relativity, Progress in Scientific Culture, 1 (1976)
• J. S. Bell, Speakable and unspeakable in quantum mechanics, Cambridge University Press (1987), ISBN 0-521-52338-9 (enthält den obigen Aufsatz von Bell von 1976)
• H. Nikolic, Relativistic contraction of an accelerated rod, Am. J. Phys. 67 (1999) 1007
• T. Matsuda and A. Kinoshita, A Paradox of Two Space Ships in Special Relativity , AAPPS Bulletin, 14 (2004) 3-7

Weblinks

• Relativity FAQ: Bell's Spaceship Paradox
• Norbert Dragon, Geometrie der Relativitätstheorie und FAQ
• Joachim Schulz: Relativistische Beschleunigung
• Austin Gleeson, Course Notes Chapter 13

Einzelnachweise

1. ↑ Bell Speakable and unspeakable in quantum mechanics, S.68. Bell fügte hinzu: Of course many people who gave this wrong answer at first get the right answer on further reflection.