- Minkowski-Kompaktum
-
Der Banach-Mazur-Abstand, benannt nach Stefan Banach und Stanisław Mazur, ist ein Begriff aus der mathematischen Theorie der Banachräume. Er definiert einen Abstand zwischen zwei isomorphen normierten Räumen und wird besonders für endlich-dimensionale Räume verwendet.
Inhaltsverzeichnis
Motivation und Definition
Sind
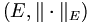 und
und 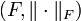 zwei isomorphe normierte Räume, so gibt es eine stetige, lineare Abbildung
zwei isomorphe normierte Räume, so gibt es eine stetige, lineare Abbildung 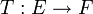 . Für die Operatornorm von T gilt
. Für die Operatornorm von T gilt 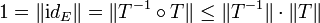 . Daher ist
. Daher ist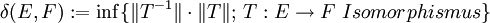
eine Zahl
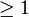 , die misst, wie weit die Räume
, die misst, wie weit die Räume 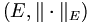 und
und 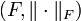 davon entfernt sind, isometrisch isomorph zu sein. Diese Zahl nennt man den Banach-Mazur-Abstand zwischen
davon entfernt sind, isometrisch isomorph zu sein. Diese Zahl nennt man den Banach-Mazur-Abstand zwischen 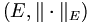 und
und 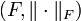 . Sind E und F nicht isomorph, so ist
. Sind E und F nicht isomorph, so ist 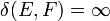 .
.Es gelten folgende einfache Regeln:
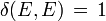 ; allgemeiner
; allgemeiner 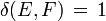 , falls E und F isometrisch isomorph sind,
, falls E und F isometrisch isomorph sind,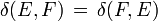 für normierte Räume E und F,
für normierte Räume E und F,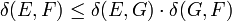 für normierte Räume E,F und G.
für normierte Räume E,F und G.
Daraus ergibt sich, dass sich
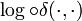 wie eine Metrik verhält, wobei log irgendeine Logarithmusfunktion ist, zum Beispiel der natürliche Logarithmus. Das erklärt den Namen Banach-Mazur-Abstand.
wie eine Metrik verhält, wobei log irgendeine Logarithmusfunktion ist, zum Beispiel der natürliche Logarithmus. Das erklärt den Namen Banach-Mazur-Abstand.Bemerkungen
Der Banach-Mazur-Abstand δ(E,F) hängt vom zu Grunde liegenden Grundkörper,
 oder
oder 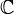 , ab. Es gibt ein auf Jean Bourgain zurückgehendes Beispiel eines reellen Banachraums mit zwei komplexen Banachraum-Strukturen, die nicht isomorph sind.
, ab. Es gibt ein auf Jean Bourgain zurückgehendes Beispiel eines reellen Banachraums mit zwei komplexen Banachraum-Strukturen, die nicht isomorph sind.Aus
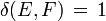 folgt im Allgemeinen nicht, dass E und F isometrisch isomorph sind. Für das folgende auf Aleksander Pelczynski und Czesław Bessaga zurückgehende Beispiel seien für
folgt im Allgemeinen nicht, dass E und F isometrisch isomorph sind. Für das folgende auf Aleksander Pelczynski und Czesław Bessaga zurückgehende Beispiel seien für 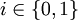 folgende Normen auf c0 definiert:
folgende Normen auf c0 definiert: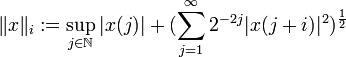
Setzt man
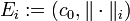 , so kann man zeigen, dass E0 strikt konvex ist, E1 aber nicht; daher können E0 und E1 nicht isometrisch isomorph sein. Setzt man
, so kann man zeigen, dass E0 strikt konvex ist, E1 aber nicht; daher können E0 und E1 nicht isometrisch isomorph sein. Setzt man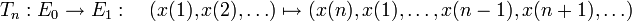 ,
,so ist
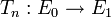 ein Isomorphismus und es ist
ein Isomorphismus und es ist 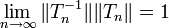 , also gilt δ(E0,E1) = 1.
, also gilt δ(E0,E1) = 1.Dieses Beispiel muss notwendiger Weise unendlich-dimensional sein, denn für zwei endlich-dimensionale Räume E und F kann man zeigen, dass δ(E,F) = 1 genau dann gilt, wenn E und F isometrisch isomorph sind.
Minkowski-Kompaktum
Es sei
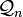 die Klasse aller n-dimensionalen Banachräume. Die isometrische Isomophie ist eine mit
die Klasse aller n-dimensionalen Banachräume. Die isometrische Isomophie ist eine mit 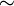 bezeichnete Äquivalenzrelation auf
bezeichnete Äquivalenzrelation auf 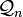 . Man kann zeigen, dass der Banach-Mazur-Abstand eine Abbildung auf der Menge
. Man kann zeigen, dass der Banach-Mazur-Abstand eine Abbildung auf der Menge 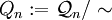 induziert und dass
induziert und dass 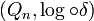 ein kompakter metrischer Raum ist, das sogenannte Minkowski-Kompaktum (nach Hermann Minkowski) oder auch Banach-Mazur-Kompaktum. Auch wenn δ keine Metrik ist, sondern nur der Logarithmus von δ, so werden metrische Begriffe im Zusammenhang mit dem Minkowski-Kompaktum häufig bezüglich δ verwendet, das gilt insbesondere für die in diesem Absatz verwendeten Begriffe Abstand und Durchmesser.
ein kompakter metrischer Raum ist, das sogenannte Minkowski-Kompaktum (nach Hermann Minkowski) oder auch Banach-Mazur-Kompaktum. Auch wenn δ keine Metrik ist, sondern nur der Logarithmus von δ, so werden metrische Begriffe im Zusammenhang mit dem Minkowski-Kompaktum häufig bezüglich δ verwendet, das gilt insbesondere für die in diesem Absatz verwendeten Begriffe Abstand und Durchmesser.Es bezeichne
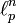 den
den  mit der p-Norm. Dann zeigt man leicht
mit der p-Norm. Dann zeigt man leicht 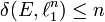 für alle
für alle 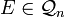 : Nach dem Auerbach-Lemma existiert eine Auerbachbasis (ei,ei')i von E. Für
: Nach dem Auerbach-Lemma existiert eine Auerbachbasis (ei,ei')i von E. Für 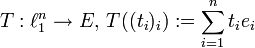 gilt dann
gilt dann 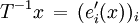 und daher
und daher 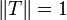 und
und 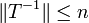 , woraus
, woraus 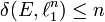 folgt.
folgt.Aufwändiger ist die 1948 von Fritz John gezeigte Ungleichung
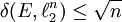 für alle
für alle 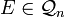 . Daraus folgt sofort
. Daraus folgt sofort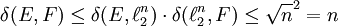 für alle
für alle 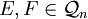 .
.Daher ist der Durchmesser des Minkowski-Kompaktums
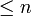 . E. D. Gluskin konnte zeigen, dass der Durchmesser nach unten durch eine Konstante mal n abgeschätzt werden kann. Es sind noch einige konkrete Abstände bekannt, so zum Beispiel
. E. D. Gluskin konnte zeigen, dass der Durchmesser nach unten durch eine Konstante mal n abgeschätzt werden kann. Es sind noch einige konkrete Abstände bekannt, so zum Beispiel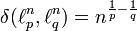 falls
falls 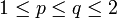 oder
oder 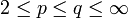 .
.Für den Fall
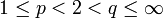 kennt man folgende Abschätzung:
kennt man folgende Abschätzung: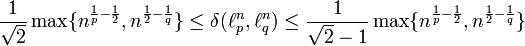 .
.Quellen
- Albrecht Pietsch: History of Banach Spaces and Linear Operators, Birkhäuser Boston (2007), ISBN 978-0-8176-4367-6
- Nicole Tomczak-Jaegermann: Banach-Mazur-Distances and Finite Dimensional Operator Ideals, Pitman monographs and Surveys in Pure and Applied Mathematics 38 (1988) ISBN 0470209828
Wikimedia Foundation.
