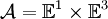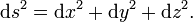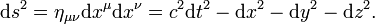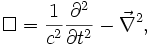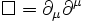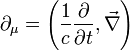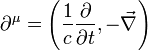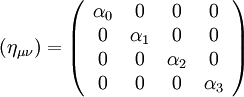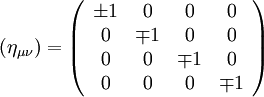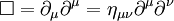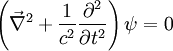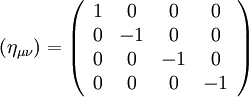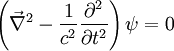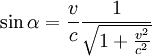Minkowski-Metrik

Die Raumzeit oder das Raum-Zeit-Kontinuum bezeichnet in der Relativitätstheorie die Vereinigung von Raum und Zeit in einer einheitlichen vierdimensionalen Struktur, in welcher die räumlichen und zeitlichen Koordinaten bei Transformationen in andere Bezugssysteme miteinander vermischt werden können.

Zwar lässt sich ein absolut gültiger Abstandsbegriff für Raumzeitpunkte (Ereignisse) definieren, jedoch ist es vom Bewegungszustand des Beobachters und der Anwesenheit von Masse bzw. Energie (z. B. in Feldern) abhängig, was davon als räumlicher und zeitlicher Abstand erscheint. Mathematisch gesehen bildet die Raumzeit eine pseudo-riemannsche Mannigfaltigkeit.

Arten von Raumzeiten

Raumzeit nach Aristoteles

Aristoteles-Raumzeit

Zur Konstruktion der Aristoteles-Raumzeit wird der Euklidsche Raum 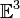$\mathbb{E}^3$ über das Schema des Aristoteles mit der Euklidschen Zeit 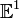$\mathbb{E}^1$ zur sog. Aristoteles-Raumzeit kombiniert:

$\mathcal{A} = \mathbb{E}^1 \times \mathbb{E}^3$

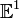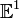Die Euklidsche Zeit $\mathbb{E}^1$ unterscheidet sich dahingehend vom Raum der reellen Zahlen $\mathbb R$, dass $\mathbb {E}^1$ keinen absolut definierten Nullpunkt aufweist. Gemeinsam ist beiden eine Orientierung (Zeitrichtung).

Der dreidimensionalen Euklidische Punktraum 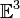$\mathbb{E}^3$ unterscheidet sich zum $\mathbb{R}^3$ darin, dass es kein vorgegebenes Koordinatensystem gibt, also weder einen definierten Ursprung, noch (nach willkürlicher Wahl eines solchen Nullpunktes) eine vorgegeben Vektorraumbasis. Gemeinsam ist beiden ein vorgegebenes Skalarprodukt, das die Othonormalbasen auszeichnet. Heute würde man diesen Raum ebenfalls als orientiert (Händigkeit) ansehen.

Galileoraum

Raumzeit nach Galileo

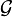Neben der Aristoteles-Raumzeit wird auch der Galileoraum $\mathcal{G}$ definiert. Dieser zeichnet sich dadurch aus, dass $\mathcal{G}$ durch kanonische Projektion auf einen beliebig gewählten Zeitraum 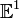$\mathbb{E}^1$, welcher als absolut definiert angenommen wird, projiziert wird.

Dieser Raum basiert auf Galileos Beobachtung, dass sich die Erde um die Sonne dreht und dennoch einem Beobachter auf der Erde vorkommt als stünde die Erde still. Auch bemerkte Galileo, dass eine Flüssigkeit auch in einem Schiff, das sich gleichmäßig bewegt, immer gerade nach unten tropft.^[1]

Das Problem wird dadurch gelöst, dass unabhängige Inertialsysteme 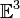$\mathbb{E}^3$ definiert werden, zu denen eine Bewegung gemessen wird. Somit hat der Beobachter auf der Erde den Eindruck, dass die Erde stillsteht und sich die Sonne um die Erde dreht, während ein Beobachter nahe der Sonne sich in einem anderen Inertialsystem befindet und damit eine Bewegung der Erde relativ zur Sonne feststellt.

Der Galileoraum zeichnet sich dadurch aus, dass zwar unterschiedliche Inertialsysteme existieren, aber nur eine absolute (d. h. allen Punkten gemeinsame) Zeit.

Newton–Cartan Raumzeit

Raumzeit nach Newton-Cartan

Élie Cartan erweiterte die Raumdefinition nach Newton um die Möglichkeit, bahnförmige Bewegungen (wie etwa die Umkreisung der Erde um die Sonne) als geradlinige Bewegungen aufzufassen, indem das Inertialsystem verschoben wird. Die von Cartan erweiterte Raumzeit wird auch als Newtonraumzeit 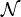$\mathcal{N}$ bezeichnet.

Raumzeit in der speziellen Relativitätstheorie

Allgemeines

In der speziellen Relativitätstheorie (SRT) werden die dreidimensionalen Raumkoordinaten (x,y,z) um eine Zeitkomponente ct zu einem Vierervektor erweitert, also (ct,x,y,z).

Im dreidimensionalen kartesischen Koordinatensystem ist der differentielle räumliche Abstand zweier Punkte

$\,\mathrm ds^2=\mathrm dx^2+\mathrm dy^2+\mathrm dz^2.$

Ein Punkt in der Raumzeit besitzt drei Raumkoordinaten sowie eine Zeitkoordinate und wird als Ereignis bezeichnet. Für Ereignisse wird ein raum-zeitlicher Abstand definiert

$\,\mathrm ds^2=\eta_{\mu\nu}\mathrm dx^\mu \mathrm dx^\nu = c^2 \mathrm dt^2 - \mathrm dx^2 - \mathrm dy^2 - \mathrm dz^2.$

Dies ist die Metrik der flachen Raumzeit der SRT mit dem metrischen Tensor 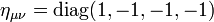$\, \eta_{\mu\nu}=\mathrm{diag}(1,-1,-1,-1)$. Sie wird auch als Minkowski-Metrik bezeichnet. Dabei ist zu beachten, dass die Minkowski-Metrik weder eine Metrik, noch eine Pseudometrik im mathematischen Sinne ist. ds heißt Linienelement und ist proportional zur Eigenzeit $c\,\mathrm d\tau=\mathrm ds$.

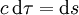Indem man fordert, dass dieser vierdimensionale Abstand (bzw. die Minkowski-Metrik) konstant (invariant) unter einer linearen Koordinatentransformation ist, definiert man die Lorentz-Transformation. Für Licht, das sich mit der Geschwindigkeit c bewegt, gilt für alle Zeiten und Bezugssysteme ds = 0. Daraus ergibt sich die Konstanz der Lichtgeschwindigkeit, das Ausgangsprinzip der speziellen Relativitätstheorie.

Zwei Ereignisse, für die das Argument der Wurzel positiv ist, sind raum-zeitlich so weit entfernt, dass ein Lichtstrahl nicht von einem zum anderen Ereignis gelangen kann. Hierzu wäre Überlichtgeschwindigkeit nötig. Da Information entweder über Licht oder Materie übertragen wird und Materie in der Relativitätstheorie niemals die Lichtgeschwindigkeit erreichen kann (und somit auch nicht schneller als diese sein kann), können solche Ereignisse niemals in einer Ursache-Wirkung-Beziehung stehen. Die Raumzeit ist also zweigeteilt: Ereignisse mit imaginärem Raumzeit-Abstand kann ein Beobachter sehen. Ereignisse, die zu weit entfernt sind und nur mit Überlichtgeschwindigkeit wahrgenommen werden können, sind prinzipiell unsichtbar.

Motivation der Minkowski-Metrik

• Betrachtet man den D'Alembert-Operator $\Box$ mit

$\Box=\frac{1}{c^2}\frac{\partial^2}{\partial t^2}-\vec\nabla^2,$

so ist zu erkennen, dass man auch abkürzend

$\Box=\partial_\mu \partial^\mu$

schreiben kann, wenn folgende zwei Vierervektoren eingeführt werden:

$\partial_\mu=\left(\frac{1}{c}\frac{\partial}{\partial t},\vec\nabla\right)$

$\partial^\mu=\left(\frac{1}{c}\frac{\partial}{\partial t},-\vec\nabla\right)$

In diesem Fall tritt die Zeit als vierte Dimension auf, die Metrik η_μν muss also eine 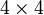$4\times 4$-Matrix sein.

• Da die vier Dimensionen linear unabhängig sind, lässt sich η_μν auf Diagonalform bringen (Hauptachsentransformation).

$(\eta_{\mu\nu})=\left(\begin{array}{cccc} \alpha_0 & 0 & 0 & 0 \\ 0 & \alpha_1 & 0 & 0 \\ 0 & 0 & \alpha_2 & 0 \\ 0 & 0 & 0 & \alpha_3 \end{array}\right)$

• Aufgrund der Forderung, dass es keine ausgezeichneten Raumzeit-Koordinaten gibt, können die Diagonalelemente nur den Wert 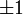$\pm 1$ besitzen. Für die Raumkoordinaten wird meist − 1 gewählt. Dies ist aber eine Konvention, die nicht einheitlich verwendet wird.

$(\eta_{\mu\nu})=\left(\begin{array}{cccc} \pm1 & 0 & 0 & 0 \\ 0 & \mp1 & 0 & 0 \\ 0 & 0 & \mp1 & 0 \\ 0 & 0 & 0 & \mp1 \end{array}\right)$

• Die Zeitkomponente kann nicht dasselbe Vorzeichen haben wie die Raumkomponenten. Hierzu betrachtet man wieder den D’Alembert-Operator $\Box$:

$\Box=\partial_\mu\partial^\mu=\eta_{\mu\nu}\partial^\mu\partial^\nu$

Daraus ergäbe sich als homogene Wellengleichung für eine Welle ψ

$\left(\vec\nabla^2+\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\psi=0$

Setzt man nun für ψ eine ebene Welle an, d. h. 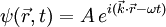$\psi(\vec r,t)=A\,e^{i(\vec k\cdot\vec r-\omega t)}$, so ergäbe sich eine komplexe Frequenz, und damit wäre ψ exponentiell gedämpft. In diesem Fall gäbe es also keine dauerhaften ebenen Wellen, was im Widerspruch zur Beobachtung steht. Folglich muss die Zeitkomponente ein anderes Vorzeichen haben:

$(\eta_{\mu\nu})=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{array}\right)$

Daraus ergibt sich die korrekte homogene Wellengleichung zu

$\left(\vec\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\psi=0$

Minkowski-Diagramm

Im Minkowski-Diagramm können die Verhältnisse geometrisch dargestellt und analysiert werden. Wegen der komplexen Eigenschaft der Zeitkomponente wird dort die Drehung der Zeitachse mit umgekehrtem Vorzeichen wie die Drehung der Koordinatenachse dargestellt.

Raumzeit in der allgemeinen Relativitätstheorie

Nichteuklidische Geometrien

Grundlage zur Beschreibung der Raumzeit (ct, x, y, z) in der allgemeinen Relativitätstheorie ist die Riemannsche Geometrie. Die Koordinatenachsen sind hier nichtlinear, was als Raumkrümmung interpretiert werden kann. Für die vierdimensionale Raumzeit werden die gleichen mathematischen Hilfsmittel wie zur Beschreibung einer zweidimensionalen Kugeloberfläche oder für Sattelflächen herangezogen. Als unumstößlich angesehene Aussagen der euklidischen Geometrie, insbesondere das Parallelenaxiom, müssen in diesen Theorien aufgegeben und durch allgemeinere Beziehungen ersetzt werden. Die kürzeste Verbindung zwischen zwei Punkten ist hier beispielsweise kein Geradenteilstück mehr. Einer Geraden in der euklidischen Geometrie entspricht die Geodäte in der nicht-euklidischen Welt; im Falle einer Kugeloberfläche sind die Geodäten die Großkreise. Die Winkelsumme im – aus Geodätenabschnitten bestehenden – Dreieck ist auch nicht mehr 180 Grad. Im Falle der Kugeloberfläche ist sie größer als 180 Grad, im Falle von Sattelflächen dagegen kleiner.

Raumzeit-Krümmung

Die Krümmung von Raum und Zeit wird durch jede Form von Energie, wie etwa Masse, Strahlung oder Druck, verursacht. Diese Größen bilden zusammen den Energie-Impuls-Tensor und gehen in die Einsteingleichungen als Quelle des Gravitationsfeldes ein. Die daraus resultierende krummlinige Bewegung von kräftefreien Körpern entlang von Geodäten wird der Gravitationsbeschleunigung zugeschrieben – in diesem Modell existiert so etwas wie eine Gravitationskraft nicht mehr. In einem infinitesimalen Raumabschnitt (lokale Karte) besitzt das erzeugte Gravitationsfeld stets die flache Metrik der speziellen Relativitätstheorie. Dies wird durch eine konstante Raumkrümmung mit dem Faktor g/c² beschrieben. Die Krümmung der Weltlinien (Bewegungskurven in der Raumzeit) aller kräftefreien Körper in diesem Raumabschnitt ist gleich.

In vielen populären Darstellungen der allgemeinen Relativitätstheorie wird häufig nicht beachtet, dass nicht nur der Raum, sondern auch die Zeit gekrümmt sein muss, um ein Gravitationsfeld zu erzeugen. Dass stets Raum und Zeit gekrümmt sein müssen, ist anschaulich leicht zu verstehen: Wäre nur der Raum gekrümmt, so wäre die Trajektorie eines geworfenen Steines immer dieselbe, egal welche Anfangsgeschwindigkeit der Stein besäße, da er stets nur dem gekrümmten Raum folgen würde. Nur durch die zusätzliche Krümmung der Zeit können die verschiedenen Trajektorien zustande kommen. Im Rahmen der ART kann dies auch mathematisch gezeigt werden.

Im normalen, dreidimensionalen Raum ist nur die Projektion der Weltlinien auf die Bewegungsebene sichtbar. Hat der Körper die Geschwindigkeit v, so ist die Weltlinie gegenüber der Zeitachse geneigt, und zwar um den Winkel tanα = v / c. Die Projektion der Bahn wird mit steigendem v um den Faktor 1 / sinα länger, der Krümmungsradius um den gleichen Faktor 1 / sinα größer, die Winkeländerung also kleiner. Die Krümmung (Winkeländerung pro Längenabschnitt) ist daher um den Faktor sin²α kleiner.

Mit

$\sin \alpha=\frac{v}{c}\frac{1}{\sqrt{1 + \frac{v^2}{c^2}}}$

folgt dann aus der Weltlinienkrümmung g/c² für die beobachtete Bahnkrümmung R im dreidimensionalen Raum

$R=\frac{g}{v^2} \cdot \left(1 + \frac{v^2}{c^2} \right)$.

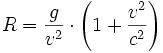Raumkrümmung und Zentrifugalbeschleunigung

Für kleine Geschwindigkeiten v≪c ist die Bahnkrümmung g/v² und entspricht damit dem Wert bei einer klassischen Zentrifugalbeschleunigung. Für Lichtstrahlen mit v=c hat der Faktor (1 + v²/c²) den Wert 2, die Krümmung entspricht also dem doppelten Wert 2g/v² der klassischen Betrachtung. Die Winkelabweichung von Sternenlicht der Fixsterne in Sonnenähe sollte also doppelt so groß sein wie im klassischen Fall. Dies wurde durch eine Afrikaexpedition zur Beobachtung der Sonnenfinsternis von 1919 durch Arthur Eddington zuerst verifiziert.

Wegen der geringen Abweichung vom klassischen Wert sind die Planetenbahnen auch keine exakten Ellipsen mehr, sondern Rosetten. An der Periheldrehung des Planeten Merkur wurde dies erstmals nachgewiesen.

Symmetrien

Die Raumzeit ist charakterisiert durch eine Anzahl von Symmetrien, die sehr wichtig für die darin geltende Physik sind. Zu diesen Symmetrien zählen neben den Symmetrien des Raumes (Translation, Rotation) auch die Symmetrien unter Lorentztransformationen (Wechsel zwischen Bezugssystemen verschiedener Geschwindigkeit). Letzteres stellt das Relativitätsprinzip sicher.

Literatur

• Sklar, L.: Space, Time, and Spacetime, University of California Press 1977 Nach wie vor die beste philosophische Einführung mit geringem technischem Apparat
• Andreas Bartels: Kausalitätsverletzungen in allgemeinrelativistischen Raumzeiten. Duncker & Humblot, Berlin 1986, ISBN 3-428-06016-4
• George F. Ellis, Ruth M. Williams: Flat and curved space-times. Oxford Univ. Press, Oxford 1992, ISBN 0-19-851164-7
• Erwin Schrödinger: Space-time structure. Cambridge Univ. Press, Cambridge 1950, deutsch: Die Struktur der Raum-Zeit., Wiss. Buchges., Darmstadt 1993, ISBN 3-534-02282-3
• Edwin F. Taylor, John Archibald Wheeler: Spacetime physics. Freeman, San Francisco 1966, ISBN 0-7167-0336-X, deutsch:Physik der Raumzeit. Spektrum Akad. Verl.,Heidelberg 1994, ISBN 3-86025-123-6
• Antonino Zichichi: From supersymmetry to the origin of space-time. World Scientific, Singapore 1995, ISBN 981-02-1917-2
• James A. Isenberg: Wheeler-Einstein-Mach spacetimes. Phys. Rev. D, VOLUME 24, NUMBER 2, 251–256, 1981
• Rainer Oloff: Geometrie der Raumzeit. Vieweg, Wiesbaden 2008, ISBN 978-3-8348-0468-6

Weblinks

• Albert Einsteins klassischer Lexikonartikel Space-Time von 1926 in der Encyclopædia Britannica

Einzelnachweise

1. ↑ Stillman Drake, Dialogue Concerning the Two Chief World Systems, Berkeley: University of California Press, 1953