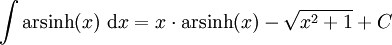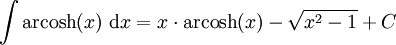- Areakosinus Hyperbolicus
-
Areasinus Hyperbolicus (abgekürzt
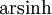 ,
, 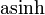 ,
, 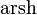 ; seltener auch
; seltener auch 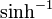 ) und Areakosinus Hyperbolicus (abgekürzt
) und Areakosinus Hyperbolicus (abgekürzt 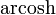 ,
, 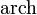 ; seltener auch
; seltener auch 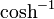 ) gehören zu den Areafunktionen und sind die Umkehrfunktionen von Sinus Hyperbolicus bzw. Kosinus Hyperbolicus.
) gehören zu den Areafunktionen und sind die Umkehrfunktionen von Sinus Hyperbolicus bzw. Kosinus Hyperbolicus.Inhaltsverzeichnis
Definitionen
Die Funktionen lassen sich durch die folgende Formeln ausdrücken:
Areasinus Hyperbolicus:Areakosinus Hyperbolicus:
Umrechnung
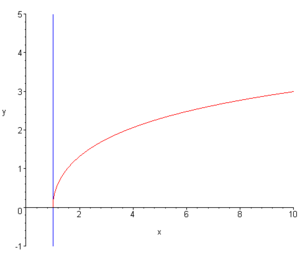
Für x > 1 gilt:Eigenschaften
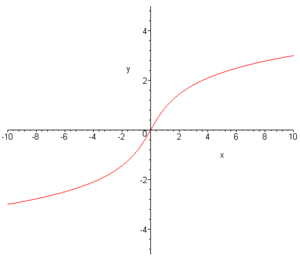
Areasinus Hyperbolicus Areakosinus Hyperbolicus Definitionsbereich 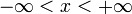
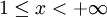
Wertebereich 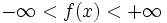
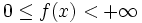
Periodizität keine keine Monotonie streng monoton steigend streng monoton steigend Symmetrien Punktsymmetrie zum Ursprung,
ungerade Funktionkeine Asymptote 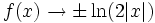 für
für 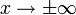
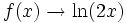 für
für 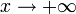
Nullstellen x = 0 x = 1 Sprungstellen keine keine Polstellen keine keine Extrema keine Minimum bei x = 1 Wendepunkte x = 0 keine Reihenentwicklungen
Wie bei allen trigonometrischen und hyperbolischen Funktionen gibt es auch Reihenentwicklungen. Dabei tritt die Doppelfakultät und die Verallgemeinerung des Binominalkoeffitienten auf.
Die Reihenentwicklungen lauten:
Ableitungen
Die Ableitung des Areasinus Hyperbolicus lautet:
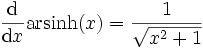 .
.
Die Ableitung des Areakosinus Hyperbolicus lautet:
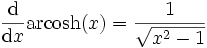 .
.
Integrale
Siehe auch
Weblinks
- Eric W. Weisstein: Inverse Hyperbolic Sine und Inverse Hyperbolic Cosine auf MathWorld (engl.)
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.

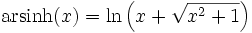
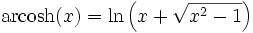
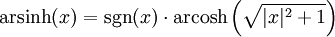
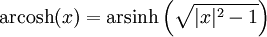
![\begin{alignat}{2}
{\rm arsinh}(x) &= x \sum_{k=0}^\infty \frac{(2k-1)!!(-x^2)^k}{(2k)!! (2k+1)} = x - \frac{1}{6} x^3 + \frac{3}{40} x^5 - \frac{15}{336} x^7 + \frac{105}{3456} x^9 - \dots & \text{ f}\ddot{\text{u}} \text{r }|x| < 1
\\
&= \sum _{k=0}^{\infty } \frac{\left(\begin{array}{c} -\frac12 \\ k \end{array} \right) x^{2 k+1}}{2 k+1} = x - \frac{1}{6} x^3 + \frac{3}{40} x^5 - \frac{5}{112} x^7 + \frac{35}{1152} x^9 - \dots & {}
\\
&= {\rm sgn}(x) \cdot \left[ \ln(2|x|) - \sum_{k=1}^\infty \frac{(2k-1)!!}{2k(2k)!!(-x^2)^k} \right] & \text{ f}\ddot{\text{u}} \text{r }|x| >1
\\
{\rm arcosh}(x) &= -\ln (x^{-1})+\ln 2-\sum_{n=1}^\infty \frac{(2n-1)!!}{2n\cdot (2n)!!}x^{-2n} & {}
\end{alignat}](/pictures/dewiki/98/b5584751a94ab79248e7aa561a5fc439.png)