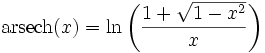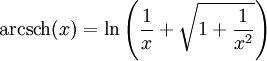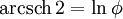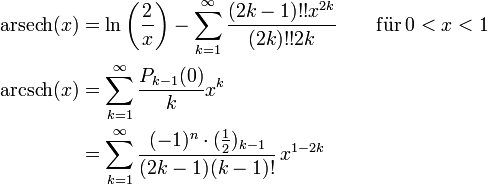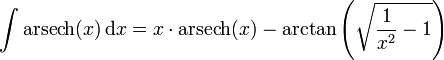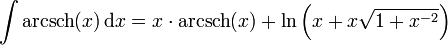Areakosekans Hyperbolikus

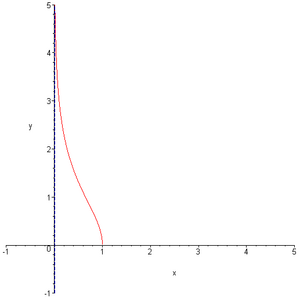
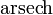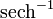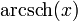Areasekans Hyperbolicus und Areakosekans Hyperbolicus gehören zu den Areafunktionen. Sie sind die Umkehrfunktionen zu Sekans Hyperbolicus bzw. Kosekans Hyperbolicus. Als Funktionen werden sie $\operatorname{arsech}$ oder seltener $\operatorname{sech}^{-1}$ bzw. $\operatorname{arcsch}(x)$ und seltener 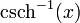$\operatorname{csch}^{-1}(x)$ geschrieben.

Definitionen

$\operatorname{arsech}(x) = \ln \left( \frac{1 + \sqrt{1-x^2}} {x} \right)$

$\operatorname{arcsch}(x) = \ln \left( \frac1x + \sqrt {1+\frac{1}{x^2}} \right)$

Eigenschaften

Graph der Funktion Areasecans Hyperbolicus

Graph der Funktion Areakosekans Hyperbolicus

	Areasecans Hyperbolicus	Areakosekans Hyperbolicus
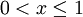
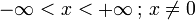
Definitionsbereich	$0 < x \le 1$	$- \infty < x < + \infty \, ; \, x\ne 0$
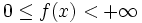
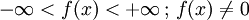
Wertebereich	$0 \le f(x) < + \infty$	$- \infty < f(x) < + \infty \, ; \, f(x) \ne 0$
Periodizität	keine	keine
Monotonie	streng monoton fallend	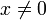$x \ne 0$ streng monoton fallend
Symmetrien	keine	Ungerade Funktion f(x) = − f( − x)
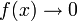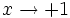
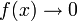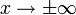
Asymptote	$f(x) \to 0$  ; $x \to +1$	$f(x) \to 0$  ; $x \to \pm \infty$
Nullstellen	x = 1	keine
Sprungstellen	keine	keine
Polstellen	x = 0	x = 0
Extrema	keine	keine
Wendepunkte	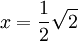$x = \frac{1}{2}\sqrt{2}$	keine

Spezielle Werte

Es gilt:

$\operatorname{arcsch}\, 2=\ln\phi$

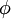wobei $\!\ \phi$ den goldenen Schnitt bezeichnet.

Reihenentwicklungen

$\begin{alignat}{2} \operatorname{arsech}(x) &= \ln \left(\frac{2}{x}\right) -\sum_{k=1}^\infty \frac{(2k-1)!! x^{2k}}{(2k)!! 2k } & \qquad \mathrm{f\ddot ur}\, 0<x<1 \\ \operatorname{arcsch}(x) &= \sum^{\infty}_{k=1} \frac{P_{k-1}(0)}{k}x^k \\ &= \sum_{k=1}^\infty \frac{(-1)^n \cdot (\tfrac12)_{k-1}}{(2k-1)(k-1)!}\,x^{1-2k} \end{alignat}$

Dabei ist P_k das k-te Legendre-Polynom und 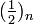$(\tfrac12)_n$ steht für das Pochhammer-Symbol.

Ableitungen

$\frac{\mathrm d}{\mathrm dx}{\rm arsech}(x)= - \frac{1}{x \sqrt{1-x^2}}$.

$\frac{\mathrm d}{\mathrm dx}\operatorname{arcsch}(x)= -\frac {1}{x\sqrt{1+x^2}}$.

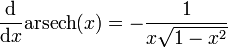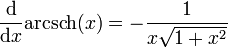Integrale

$\int\operatorname{arsech}(x)\, \mathrm dx = x\cdot\operatorname{arsech}(x) - \arctan\left(\sqrt{\frac{1}{x^2}-1}\right)$

$\int\operatorname{arcsch}(x)\, \mathrm dx = x\cdot\operatorname{arcsch}(x) + \ln\left( x+x\sqrt {1+{x}^{-2}}\right)$

Weblinks

• Eric W. Weisstein: Inverse Hyperbolic Secant und Inverse Hyperbolic Cosecant auf MathWorld

Trigonometrische Funktion

Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und Kosekans 

Umkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und Arkuskosekans 

Hyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans Hyperbolicus 

Areafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus